高考数学专题复习课件：2-7 函数的图象 59页

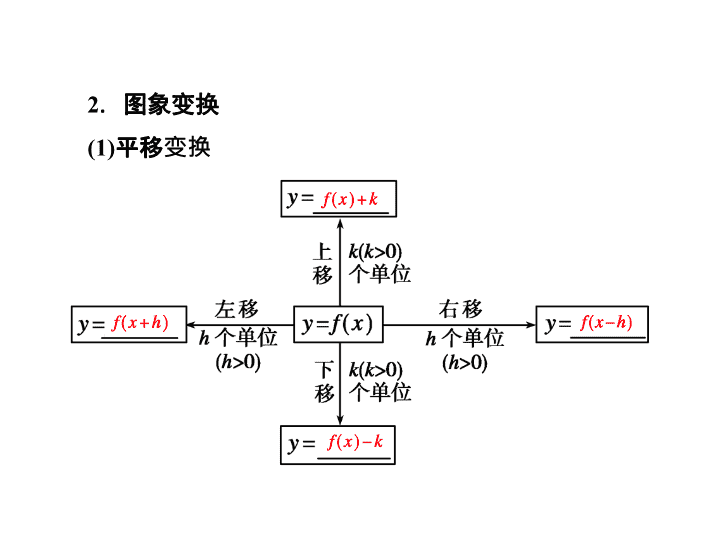
§2.7 　函数的图象 [ 考纲要求 ] 　 1. 在实际情境中，会根据不同的需要选择图象法、列表法、解析法表示函数 .2. 会运用函数图象理解和研究函数的性质，解决方程解的个数与不等式解的问题． 1 ． 利用描点法作函数图象 基本步骤是列表、描点、连线． 首先： (1) 确定函数的定义域； (2) 化简函数解析式； (3) 讨论函数的性质 ( 奇偶性、单调性、周期性、对称性等 ) ． 其次：列表 ( 尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等 ) ，描点，连线． 2 ． 图象变换 (1) 平移变换 【 思考辨析 】 　判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) 当 x ∈ (0 ，＋ ∞ ) 时，函数 y ＝ | f ( x )| 与 y ＝ f (| x |) 的图象相同． ( 　　 ) (2) 函数 y ＝ af ( x ) 与 y ＝ f ( ax )( a ＞ 0 且 a ≠ 1) 的图象相同． ( 　　 ) (3) 函数 y ＝ f ( x ) 与 y ＝－ f ( x ) 的图象关于原点对称． ( 　　 ) (4) 若函数 y ＝ f ( x ) 满足 f (1 ＋ x ) ＝ f (1 － x ) ，则函数 f ( x ) 的图象关于直线 x ＝ 1 对称． ( 　　 ) (5) 将函数 y ＝ f ( － x ) 的图象向右平移 1 个单位得到函数 y ＝ f ( － x － 1) 的图象． ( 　　 ) 【 答案 】 (1) × 　 (2) × 　 (3) × 　 (4) √ 　 (5) × 【 答案 】 D 2 ．函数 f ( x ) 的图象向右平移 1 个单位长度，所得图象与曲线 y ＝ e x 关于 y 轴对称，则 f ( x ) 的解析式为 ( 　　 ) A ． f ( x ) ＝ e x ＋ 1 　　　　　　　 B ． f ( x ) ＝ e x － 1 C ． f ( x ) ＝ e － x ＋ 1 D ． f ( x ) ＝ e － x － 1 【 解析 】 与 y ＝ e x 图象关于 y 轴对称的函数为 y ＝ e － x . 依题意， f ( x ) 图象向右平移一个单位，得 y ＝ e － x 的图象． ∴ f ( x ) 的图象由 y ＝ e － x 的图象向左平移一个单位得到． ∴ f ( x ) ＝ e － ( x ＋ 1) ＝ e － x － 1 . 【 答案 】 D 【 答案 】 D 4 ． ( 教材改编 ) 点 P 从点 O 出发，按逆时针方向沿周长为 l 的图形运动一周， O ， P 两点连线的距离 y 与点 P 走过的路程 x 的函数关系如图，那么点 P 所走的图形是 ( 　　 ) 【 答案 】 C 【 解析 】 当 x ≤ 0 时， 0 ＜ 2 x ≤ 1 ，所以由图象可知要使方程 f ( x ) － a ＝ 0 有两个实根，即函数 y ＝ f ( x ) 与 y ＝ a 的图象有两个交点，所以由图象可知 0 ＜ a ≤ 1. 【 答案 】 (0 ， 1] (2) 将函数 y ＝ log 2 x 的图象向左平移 1 个单位，再将 x 轴下方的部分沿 x 轴翻折上去，即可得到函数 y ＝ |log 2 ( x ＋ 1)| 的图象，如图． 【 方法规律 】 函数图象的画法 (1) 直接法：当函数表达式 ( 或变形后的表达式 ) 是熟悉的基本函数时，就可根据这些函数的特征找出图象的关键点直接作出图象． (2) 转化法：含有绝对值符号的函数，可脱掉绝对值符号，转化为分段函数来画图象． (3) 图象变换法：若函数图象可由某个基本函数的图象经过平移、翻折、对称得到，可利用图象变换作出，但要注意变换顺序，对不能直接找到熟悉的基本函数的要先变形，并应注意平移变换的顺序对变换单位及解析式的影响． 题型二　识图与辨图 【 例 2 】 (1) (2015· 课标全国 Ⅱ ) 如图，长方形 ABCD 的边 AB ＝ 2 ， BC ＝ 1 ， O 是 AB 的中点，点 P 沿着边 BC ， CD 与 DA 运动，记 ∠ BOP ＝ x . 将动点 P 到 A ， B 两点距离之和表示为 x 的函数 f ( x ) ，则 y ＝ f ( x ) 的图象大致为 ( 　　 ) (2) (2016· 课标全国 Ⅰ ) 函数 y ＝ 2 x 2 － e | x | 在 [ － 2 ， 2] 的图象大致为 ( 　　 ) (2) 利用导数研究函数 y ＝ 2 x 2 － e | x | 在 [0 ， 2] 上的图象，利用排除法求解． ∵ f ( x ) ＝ 2 x 2 － e | x | ， x ∈ [ － 2 ， 2] 是偶函数， 又 f (2) ＝ 8 － e 2 ∈ (0 ， 1) ，故排除 A ， B. 设 g ( x ) ＝ 2 x 2 － e x ，则 g ′( x ) ＝ 4 x － e x . 又 g ′(0) ＜ 0 ， g ′ (2) ＞ 0 ， ∴ g ( x ) 在 (0 ， 2) 内至少存在一个极值点， ∴ f ( x ) ＝ 2 x 2 － e | x | 在 (0 ， 2) 内至少存在一个极值点，排除 C. 故选 D. 【 答案 】 (1)B 　 (2)D 【 方法规律 】 函数图象的识辨可从以下方面入手： (1) 从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置； (2) 从函数的单调性，判断图象的变化趋势； (3) 从函数的奇偶性，判断图象的对称性； (4) 从函数的周期性，判断图象的循环往复； (5) 从函数的特征点，排除不合要求的图象． 跟踪训练 2 (1) (2017· 南昌二模 ) 现有四个函数： ① y ＝ x sin x ； ② y ＝ x cos x ； ③ y ＝ x |cos x | ； ④ y ＝ x · 2 x 的图象 ( 部分 ) 如下，但顺序被打乱，则按照从左到右将图象对应的函数序号安排正确的一组是 ( 　　 ) A ． ④①②③ 　　　　　　　 B ． ①④③② C ． ③④②① D ． ①④②③ (2) 如图，圆 O 的半径为 1 ， A 是圆上的定点， P 是圆上的动点，角 x 的始边为射线 OA ，终边为射线 OP ，过点 P 作直线 OA 的垂线，垂足为 M ，将点 M 到直线 OP 的距离表示成 x 的函数 f ( x ) ，则 y ＝ f ( x ) 在 [0 ， π ] 的图象大致为 ( 　　 ) 【 解析 】 (1) 由于函数 y ＝ x sin x 是偶函数，由图象知，函数 ① 对应第一个图象；函数 y ＝ x cos x 是奇函数，且当 x ＝ π 时， y ＝－ π ＜ 0 ，故函数 ② 对应第三个图象；函数 y ＝ x |cos x | 为奇函数，故函数 ③ 与第四个图象对应；函数 y ＝ x ·2 x 为非奇非偶函数，与第二个图象对应．综上可知，选 D. 【 答案 】 (1)D 　 (2)C (2) (2015· 北京 ) 如图，函数 f ( x ) 的图象为折线 ACB ，则不等式 f ( x ) ≥ log 2 ( x ＋ 1) 的解集是 ( 　　 ) (2) 作出函数 y ＝ log 2 ( x ＋ 1) 的图象，如图所示： 其中函数 f ( x ) 与 y ＝ log 2 ( x ＋ 1) 的图象的交点为 D (1 ， 1) ，结合图象可知 f ( x ) ≥ log 2 ( x ＋ 1) 的解集为 { x | － 1 ＜ x ≤ 1} ，故选 C. 【 答案 】 (1)B 　 (2)C 【 方法规律 】 (1) 利用函数的图象研究函数的性质对于已知或易画出其在给定区间上图象的函数，其性质 ( 单调性、奇偶性、周期性、最值 ( 值域 ) 、零点 ) 常借助于图象研究，但一定要注意性质与图象特征的对应关系． (2) 利用函数的图象可解决某些方程和不等式的求解问题，方程 f ( x ) ＝ g ( x ) 的根就是函数 f ( x ) 与 g ( x ) 图象交点的横坐标；不等式 f ( x ) ＜ g ( x ) 的解集是函数 f ( x ) 的图象位于 g ( x ) 图象下方的点的横坐标的集合，体现了数形结合思想． 跟踪训练 3 已知函数 f ( x ) ＝ x | m － x |( x ∈ R) ，且 f (4) ＝ 0. (1) 求实数 m 的值； (2) 作出函数 f ( x ) 的图象； (3) 根据图象指出 f ( x ) 的单调递减区间； (4) 根据图象写出不等式 f ( x ) ＞ 0 的解集； (5) 求当 x ∈ [1 ， 5) 时函数的值域． (3) f ( x ) 的单调递减区间是 [2 ， 4] ． (4) 由图象可知， f ( x ) ＞ 0 的解集为 { x |0 ＜ x ＜ 4 或 x ＞ 4} ． (5) ∵ f (5) ＝ 5 ＞ 4 ， ∴ 由图象知，函数在 [1 ， 5) 上的值域为 [0 ， 5) ． 高频小考点 3 高考中的函数图象及应用问题 一、已知函数解析式确定函数图象 【 典例 】 (2017· 北京海淀区期中测试 ) 函数 f ( x ) ＝ 2 x ＋ sin x 的部分图象可能是 ( 　　 ) 【 思维点拨 】 根据函数的定义域、值域、单调性、奇偶性和特征点确定函数图象． 【 答案 】 A 【 温馨提醒 】 (1) 确定函数的图象，要从函数的性质出发，利用数形结合的思想． (2) 对于给出图象的选择题，可以结合函数的某一性质或特殊点进行排除． 二、函数图象的变换问题 【 典例 】 (2017· 河南平顶山二模 ) 已知函数 y ＝ a ＋ sin bx ( b ＞ 0 且 b ≠ 1) 的图象如图所示，那么函数 y ＝ log b ( x － a ) 的图象可能是 ( 　　 ) 【 答案 】 C 【 温馨提醒 】 (1) 对图象的变换问题，从 f ( x ) 到 f ( ax ＋ b ) ，可以先进行平移变换，也可以先进行伸缩变换，要注意变换过程中两者的区别． (2) 图象变换也可利用特征点的变换进行确定． 由图象可知，当 a ＜ 0 时， y ＝ f ( x ) － g ( x ) 恰有两个不同的零点；当 0 ＜ a ＜ 1 时， y ＝ f ( x ) － g ( x ) 恰有两个不同的零点；当 a ＝ 1 时， y ＝ f ( x ) － g ( x ) 只有一个零点；当 a ＞ 1 时， y ＝ f ( x ) － g ( x ) 没有零点．综上，实数 a 的取值范围是 ( － ∞ ， 0) ∪ (0 ， 1) ． 【 答案 】 D 【 温馨提醒 】 (1) 本题求解利用了数形结合的思想，数形结合的思想包括 “ 以形助数 ” 或 “ 以数辅形 ” 两个方面，本题属于 “ 以形助数 ” ，是指把某些抽象的问题直观化、生动化，能够变抽象思维为形象思维，解释数学问题的本质． (2) 利用函数图象也可以确定不等式解的情况，解题时可对方程或不等式适当变形，选择合适的函数进行作图 . ► 方法与技巧 1 ．列表描点法是作函数图象的辅助手段，要作函数图象首先要明确函数图象的位置和形状： (1) 可通过研究函数的性质如定义域、值域、奇偶性、周期性、单调性等等； (2) 可通过函数图象的变换如平移变换、对称变换、伸缩变换等． 2 ．合理处理识图题与用图题 (1) 识图 对于给定函数的图象，要从图象的左右、上下分布范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性，注意图象与函数解析式中参数的关系． (2) 用图 函数图象形象地显示了函数的性质，为研究数量关系问题提供了 “ 形 ” 的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．常用函数图象研究含参数的方程或不等式解集的情况．