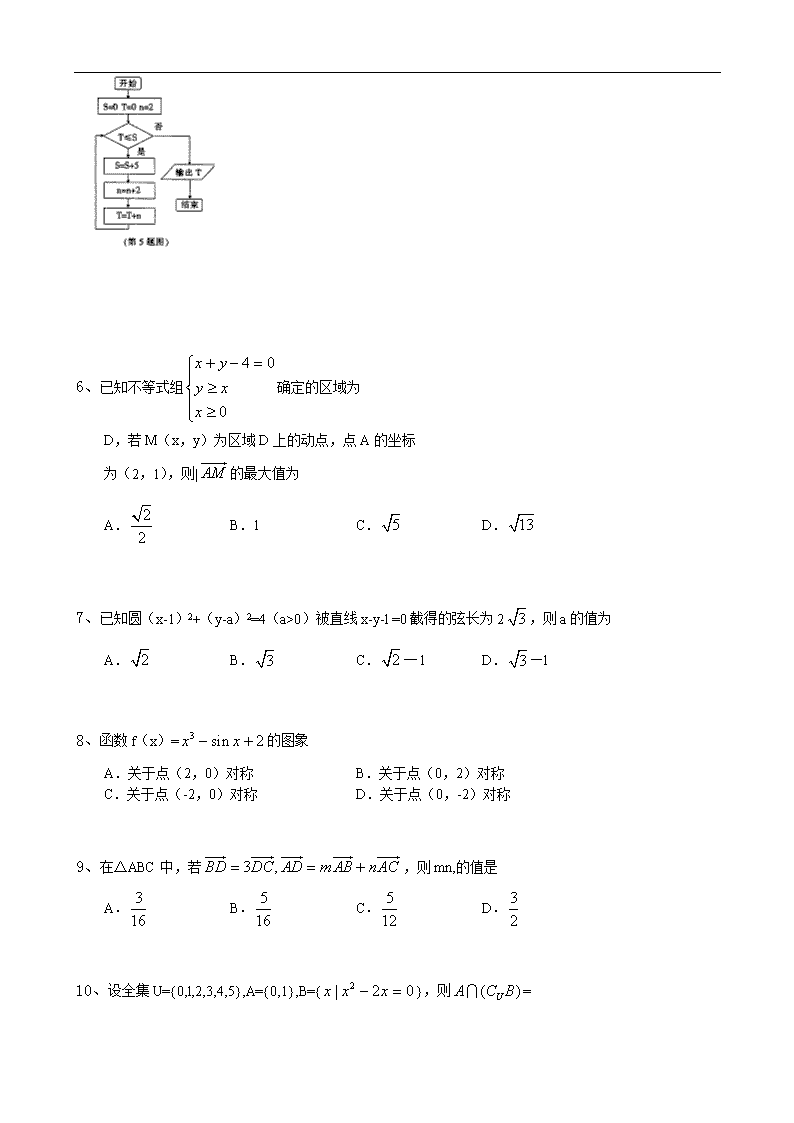福建省厦门市2012年高中毕业班适应性考试（文）试题 11页

福建省厦门市2012年高中毕业班适应性考试（文）试题 一、选择题 ‎1、已知{}是斐波那契数列，满足中各项除以4所得余数按原顺序构成的数列记为{}，则b2012=‎ ‎ A．0 B．1 C．2 D．3‎ ‎2、命题“”的否定是 ‎ A．∈R，≤0 B．≤0‎ ‎ C．<0 D．∈R，<0 ‎ ‎3、右边茎叶图的数据是10名学生1分钟跳绳的成绩，则这10名学生 ‎ 1分钟跳绳成绩的中位数是 ‎ A．173 B．174 C．175 D．179‎ ‎4、已知a∈（），且cos，则tan=‎ ‎ A． B．一 C．-2 D．2‎ ‎5、执行右图中的程序框图，输出的T值为 ‎ A．4 B．10 ‎ ‎ C．18 D．20‎ ‎6、已知不等式组确定的区域为 ‎ D，若M（x，y）为区域D上的动点，点A的坐标 为（2，1），则|的最大值为 ‎ A． B．1 C． D．‎ ‎7、已知圆（x-1）2+（y-a）2=4（a>0）被直线x-y-l =0截得的弦长为2，则a的值为 ‎ A． B． C．一l D．—l ‎8、函数f（x）=的图象 ‎ A．关于点（2，0）对称 B．关于点（0，2）对称 ‎ C．关于点（-2，0）对称 D．关于点（0，-2）对称 ‎9、在△ABC中，若，则mn,的值是 ‎ A． B． C． D．‎ ‎10、设全集U={0,l,2,3,4,5},A={0,1},B={}，则=‎ ‎ A． B．{3,4} C．{1,3,5} D．{l}‎ ‎11、已知双曲线的左、右焦点分别是F1、F2，点B（0，b），若△BF1F2的外接圆圆心到双曲线渐近线的距离为，则双曲线的离心率为 ‎ A． B． C．2 D．2‎ ‎12、函数y=sin（x十）在一个周期内的图象如图所示，M、N 分别是最高、最低点，O为坐标原点且，则函 ‎ 数的最小正周期为 ‎ A． B． C．3 D．4‎ 二、填空题 ‎13、设i为虚数单位，若为实数，则实数a的值为 ．‎ ‎14、如图，曲线OB的方程为（0≤x≤1），为估计阴影部 分的面积，采用随机模拟方式产生菇∈（0，1），y∈（0，1）的 ‎200个点（x，y），经统计，落在阴影部分的点共134个，则估 计阴影部分的面积是 ．‎ ‎15、一个几何体的三视图如图所示，其中正视图是腰长为2的等 ‎ 腰三角形，俯视图是半径为1的半圆，则该几何体的表面积 ‎ 是 ．‎ ‎16、已知函数在x=1处的切 ‎ 线与x轴平行，若函数f(x）的图象经过四个象限，则实数a ‎ 的取值范围是 ，‎ 三、解答题 ‎17、‎ ‎ 已知：‎ ‎ （I）若，求a的值；‎ ‎ （Ⅱ）已知a>e -1，若在[1，e]（e=2．718…）上存在一点0。，使得成立，求a的取值范围；‎ ‎ （Ⅲ）设函数的图象C1与函数+bx的图象C2交于点A、B，过线段A、B的中点M作x轴的垂线分别交C1、C2于点P、Q，问是否存在点M使C1在P处的切线与C2在Q 处的切线平行？若存在，求出M的横坐标；若不存在，请说明理由，‎ ‎18、‎ ‎ 已知三棱柱ADF - BCE中，DF⊥平面ABCD，G是DF的中点．‎ ‎ （I）求证：BF∥平面ACG;‎ ‎ （Ⅱ）若AD =DF =1，AB =2，∠DAB= 60°，求三棱锥B -ADF的体积．‎ ‎19、为了解某居住小区住户的年收入和年饮食支出的关系，抽取了其中5户家庭的调查数据如下表：‎ ‎ （I）根据表中数据用最小二乘法求得回归直线方程=bx +a中的6=0．31，请预测年收入为9万元家庭的年饮食支出；‎ ‎ （Ⅱ）从5户家庭中任选2户，求“恰有一户家庭年饮食支出小于1．6万元”的概率．‎ ‎20、等差数列{}的前n项和为；等比数列{}中，．若，b2S2=12．‎ ‎ （I）求与；‎ ‎ （Ⅱ）设，数列{cn}的前n项和为Tn．求证：≥3n．‎ ‎21、已知锐角△ABC中，内角A、B、C的对边分别为a、b、c，且c2=ab．‎ ‎ （I）求角C的大小；‎ ‎ （Ⅱ）设函数且直线y=图象相邻两交点间的距离为，求f(A）的取值范围．‎ ‎22、‎ ‎ 某公园内有一椭圆形景观水池，经测量知，椭圆长轴长为20米，短轴长为16米．现以椭圆长轴所在直线为x轴，短轴所在直线为y轴，建立平面直角坐标系，如图所示．‎ ‎ （I）为增加景观效果，拟在水池内选定两点安装水雾喷射口，要求椭圆上各点到这两点距离之和都相等，请指出水雾喷射口的位置（用坐标表示），并求椭圆的方程；‎ ‎ （Ⅱ）为增强水池的观赏性，拟划出一个以椭圆的长轴顶点A、短轴顶点B及椭圆上某点M构成的三角形区域进行夜景灯光布置．请确定点肘的位置，使此三角形区域面积最大．‎ 以下是答案 一、选择题 ‎1、 B ‎2、 C ‎3、 B ‎4、 D ‎5、 C ‎6、 D ‎7、 A ‎8、 B ‎9、 A ‎10、 D ‎11、 C ‎12、 C 二、填空题 ‎13、‎ ‎14、‎ ‎15、‎ ‎16、‎ 三、解答题 ‎17、 ‎ ‎ ‎ ‎18、 ‎ ‎19、‎ ‎20、‎ ‎21、‎ ‎22、‎