高中数学必修4公开课教案2_5_2 向量在物理中的应用举例 5页

‎2.5.2 向量在物理中的应用举例 整体设计 教学分析 ‎ 向量与物理学天然相联.向量概念的原型就是物理中的力、速度、位以及几何中的有向线段等概念,向量是既有大小、又有方向的量,它与物理学中的力学、运动学等有着天然的联系,将向量这一工具应用到物理中,可以使物理题解答更简捷、更清晰.并且向量知识不仅是解决物理许多问题的有利工具,而且用数学的思想方法去审视相关物理现象,研究相关物理问题,可使我们对物理问题的认识更深刻.物理中有许多量,比如力、速度、加速度、位移等都是向量,这些物理现象都可以用向量来研究.‎ ‎ 用向量研究物理问题的相关知识.(1)力、速度、加速度、位移等既然都是向量,那么它们的合成与分解就是向量的加、减法,运动的叠加亦用到向量的合成;(2)动量是数乘向量;(3)功即是力与所产生位移的数量积.‎ ‎ 用向量知识研究物理问题的基本思路和方法.①通过抽象、概括,把物理现象转化为与之相关的向量问题;②认真分析物理现象,深刻把握物理量之间的相互关系;③利用向量知识解决这个向量问题,并获得这个向量的解;④利用这个结果,对原物理现象作出合理解释,即用向量知识圆满解决物理问题.教学中要善于引导学生通过对现实原型的观察、分析和比较,得出抽象的数学模型.例如,物理中力的合成与分解是向量的加法运算与向量分解的原型.同时,注重向量模型的运用,引导解决现实中的一些物理和几何问题.这样可以充分发挥现实原型对抽象的数学概念的支撑作用.‎ 三维目标 ‎1.通过力的合成与分解的物理模型,速度的合成与分解的物理模型,掌握利用向量方法研究物理中相关问题的步骤,明了向量在物理中应用的基本题型,进一步加深对所学向量的概念和向量运算的认识.‎ ‎2.通过对具体问题的探究解决,进一步培养学生的数学应用意识,提高应用数学的能力.体会数学在现实生活中的重要作用.养成善于发现生活中的数学,善于发现物理及其他科目中的数学及思考领悟各学科之间的内在联系的良好习惯.‎ 重点难点 教学重点:1.运用向量的有关知识对物理中力的作用、速度的分解进行相关分析和计算.2.归纳利用向量方法解决物理问题的基本方法.‎ 教学难点:将物理中有关矢量的问题转化为数学中向量的问题.‎ 课时安排 ‎1课时 教学过程 导入新课 ‎ 思路1.(章头图引入)章头图中,道路、路标体现了向量与位移、速度、力等物理量之间的密切联系.章引言说明了向量的研究对象及研究方法.那么向量究竟是怎样应用于物理的呢？它就像章头图中的高速公路一样,是一条解决物理问题的高速公路.在学生渴望了解的企盼中,教师展示物理模型,由此展开新课.‎ ‎ 思路2.(问题引入)你能举出物理中的哪些向量?比如力、位移、速度、加速度等,既有大小又有方向,都是向量,学生很容易就举出来.进一步,你能举出应用向量来分析和解决物理问题的例子吗?你是怎样解决的？教师由此引导:向量是有广泛应用的数学工具,对向量在物理中的研究,有助于进一步加深对这方面问题的认识.我们可以通过对下面若干问题的研究,体会向量在物理中的重要作用.由此自然地引入新课.‎ 应用示例 例1 在日常生活中,你是否有这样的经验:两个人共提一个旅行包,夹角越大越费力;在单杠上做引体向上运动,两臂的夹角越小越省力.你能从数学的角度解释这种现象吗?‎ ‎ 活动:这个日常生活问题可以抽象为如图1所示的数学模型,引导学生由向量的平行四边形法则,力的平衡及解直角三角形等知识来思考探究这个数学问题.这样物理中力的现象就转化为数学中的向量问题.只要分析清楚F、G、θ三者之间的关系(其中F为F1、F2的合力),就得到了问题的数学解释.‎ 图1‎ 在教学中要尽可能地采用多媒体,在信息技术的帮助下让学生来动态地观察|F|、|G|、θ之间在变化过程中所产生的相互影响.由学生独立完成本例后,与学生共同探究归纳出向量在物理中的应用的解题步骤,也可以由学生自己完成,还可以用信息技术来验证.‎ ‎ 用向量解决物理问题的一般步骤是:①问题的转化,即把物理问题转化为数学问题;②模型的建立,即建立以向量为主体的数学模型;③参数的获得,即求出数学模型的有关解——理论参数值;④问题的答案,即回到问题的初始状态,解释相关的物理现象.‎ 解:不妨设|F1|=|F2|,由向量的平行四边形法则、力的平衡以及直角三角形的知识,可以知道 ‎ 通过上面的式子,我们发现:当θ由0°到180°逐渐变大时,由0°到90°逐渐变大,cos的值由大逐渐变小,因此|F1|由小逐渐变大,即F1,F2之间的夹角越大越费力,夹角越小越省力.‎ ‎ 点评:本例是日常生活中经常遇到的问题,学生也会有两人共提一个旅行包以及在单杠上做引体向上运动的经验.本例的关键是作出简单的受力分析图,启发学生将物理现象转化成模型,从数学角度进行解释,这就是本例活动中所完成的事情.教学中要充分利用好这个模型,为解决其他物理问题打下基础.得到模型后就可以发现,这是一个很简单的向量问题,这也是向量工具优越性的具体体现.‎ 变式训练 ‎ 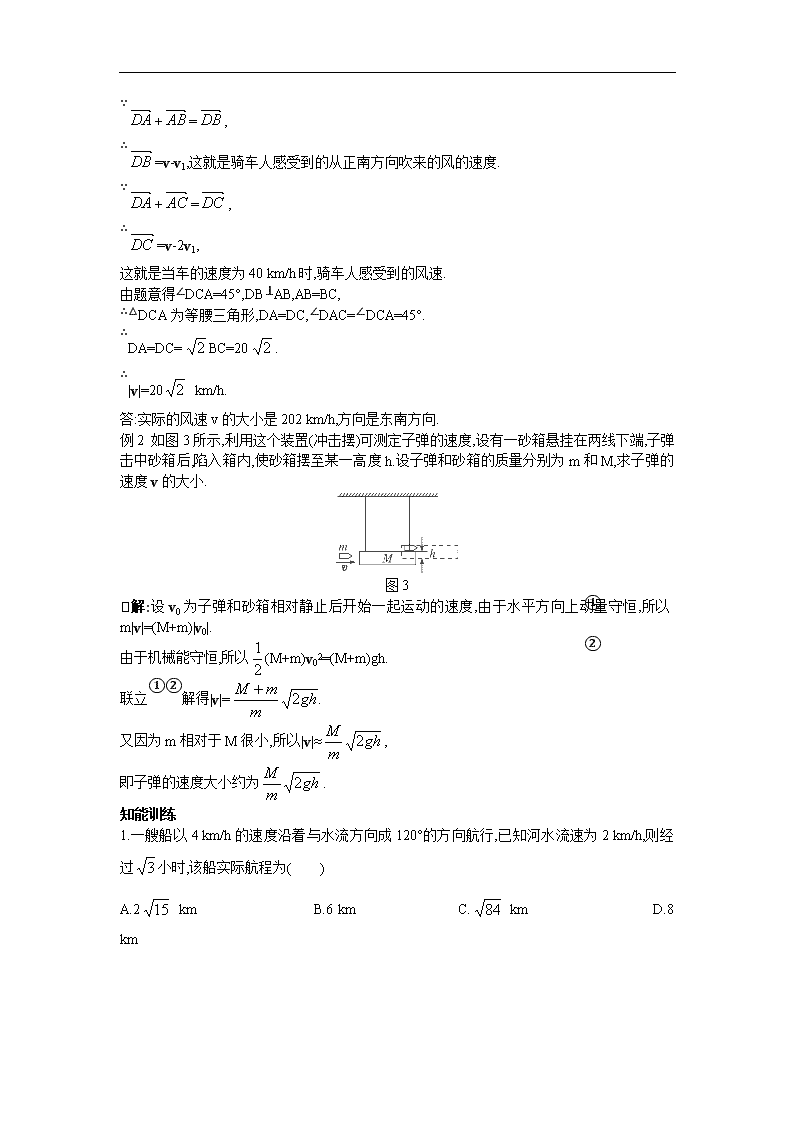某人骑摩托车以20 km/h的速度向西行驶,感到风从正南方向吹来,而当其速度变为40 km/h时,他又感到风从西南方向吹来,求实际的风向和风速.‎ 图2‎ 解:如图2所示.设v1表示20 km/h的速度,在无风时,此人感到的风速为-v1,实际的风速为v,那么此人所感到的风速为v+(-v1)=v-v1.‎ 令=-v1,=-2v1,实际风速为v.‎ ‎∵+=,‎ ‎∴=v-v1,这就是骑车人感受到的从正南方向吹来的风的速度.‎ ‎∵+=,‎ ‎∴=v-2v1,‎ 这就是当车的速度为40 km/h时,骑车人感受到的风速.‎ 由题意得∠DCA=45°,DB⊥AB,AB=BC,‎ ‎∴△DCA为等腰三角形,DA=DC,∠DAC=∠DCA=45°.‎ ‎∴DA=DC=BC=20.‎ ‎∴|v|=20 km/h.‎ 答:实际的风速v的大小是202 km/h,方向是东南方向.‎ 例2 如图3所示,利用这个装置(冲击摆)可测定子弹的速度,设有一砂箱悬挂在两线下端,子弹击中砂箱后,陷入箱内,使砂箱摆至某一高度h.设子弹和砂箱的质量分别为m和M,求子弹的速度v的大小.‎ 图3‎ 解:设v0为子弹和砂箱相对静止后开始一起运动的速度,由于水平方向上动量守恒,所以m|v|=(M+m)|v0|. ①‎ 由于机械能守恒,所以(M+m)v02=(M+m)gh. ②‎ 联立①②解得|v|=‎ 又因为m相对于M很小,所以|v|≈,‎ 即子弹的速度大小约为.‎ 知能训练 ‎1.一艘船以4 km/h的速度沿着与水流方向成120°的方向航行,已知河水流速为2 km/h,则经过小时,该船实际航程为( )‎ A.2 km B.6 km C. km D.8 km 图4‎ ‎2.如图4,已知两个力的大小和方向,则合力的大小为 N;若在图示坐标系中,用坐标表示合力F,则F=___________.‎ ‎3.一艘船以5 km/h的速度向垂直于对岸的方向行驶,而该船实际航行的方向与水流方向成30°角,求水流速度与船的实际速度.‎ 解答:‎ ‎1.B 点评:由于学生还没有学习正弦定理和余弦定理,所以要通过作高来求.‎ ‎2. (5,4)‎ 图5‎ ‎3.如图5所示,设表示水流速度,表示船垂直于对岸的速度,表示船的实际速度,∠AOC=30°,||=5 km/h.‎ 因为OACB为矩形,所以||=||·cot30°=||·cot30°=53≈8.66 km/h,‎ ‎||===10 km/h.‎ 答:水流速度为8.66 km/h,船的实际速度为10 km/h.‎ 点评:转化为数学模型,画出向量图,在直角三角形中解出.‎ 课堂小结 ‎1.与学生共同归纳总结利用向量解决物理问题的步骤.‎ ‎①问题的转化,即把物理问题转化为数学问题;‎ ‎②模型的建立,即建立以向量为主体的数学模型;‎ ‎③参数的获得,即求出数学模型的有关解——理论参数值;‎ ‎④问题的答案,即回到问题的初始状态,解释相关的物理现象.‎ ‎2.与学生共同归纳总结向量在物理中应用的基本题型.‎ ‎①力、速度、加速度、位移都是向量;‎ ‎②力、速度、加速度、位移的合成与分解对应相应向量的加减;‎ ‎③)动量mv是数乘向量,冲量ΔtF也是数乘向量;‎ ‎④功是力F与位移s的数量积,即W=F·s.‎ 作业 ‎1.课本习题2.5 A组3、4,B组1、2.‎ ‎2.归纳总结物理学中哪些地方可用向量.‎ 设计感想 ‎1.本教案设计的指导思想是:由于本节重在解决两个问题,一是如何把物理问题转化成数学问题,也就是将物理量之间的关系抽象成数学模型;二是如何用建立起来的数学模型解释和回答相关的物理现象.因此本教案设计的重点也就放在怎样让学生探究解决这两个问题上.而把这个探究的重点又放在这两个中的第一个上,也就是引导学生认真分析物理现象、准确把握物理量之间的相互关系.通过抽象、概括,把物理现象转化为与之相关的向量问题,然后利用向量知识解决这个向量问题.‎ ‎2.经历是最好的老师.充分让学生经历分析、探究并解决实际问题的过程,这也是学习数学,领悟思想方法的最好载体.学生这种经历的实践活动越多,解决实际问题的方法就越恰当而简捷.教科书中对本节的两个例题的处理方法,都不是先给出解法,而是先进行分析,探索出解题思路,再给出解法,就足以说明这一点.‎ ‎3.突出数形结合的思想.教科书例题都是先画图进行分析的,本教案的设计中也突出了这一点.让学生在活动的时候就先想到画图,并在这个活动中,体会数形结合的应用,体会数学具有广泛的应用,体会向量这个工具的优越性.‎