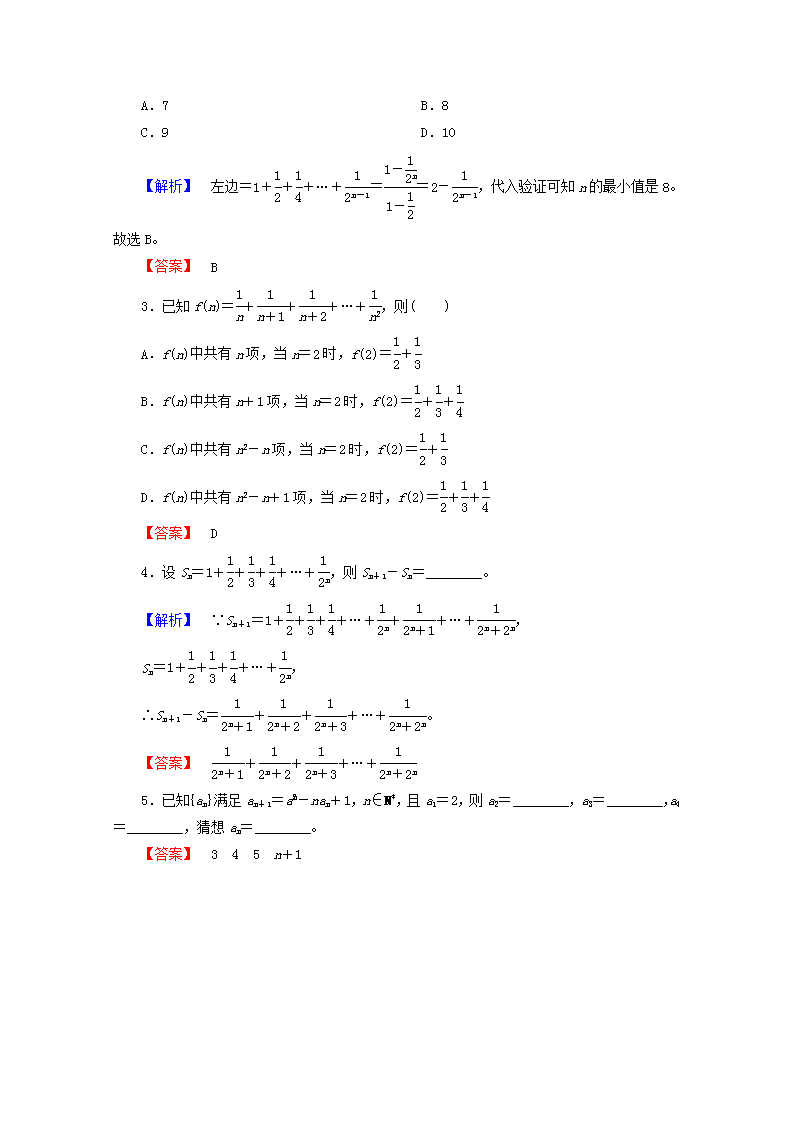【数学】2018届一轮复习北师大版第六章不等式推理与证明第七节数学归纳法教案 9页

第七节　数学归纳法 ‎☆☆☆2017考纲考题考情☆☆☆‎ 考纲要求 真题举例 命题角度 ‎1.了解数学归纳法的原理；‎ ‎2.能用数学归纳法证明一些简单的数学命题。‎ 全国卷Ⅰ，Ⅱ，Ⅲ无 ‎2015江苏，23,10分(数学归纳法)‎ ‎2014，安徽，21,13分(数学归纳法)‎ ‎2014，陕西，21,14分(数学归纳法)‎ ‎　　数学归纳法在近年的全国卷高考中还未出现过，只是在个别的自主命题的省份有所考查。由此可见数学归纳法不是高考的热点内容，我们做一般地认识就可以了，不必搞得过深过难。‎ 微知识　小题练 自|主|排|查 数学归纳法的定义及框图表示 ‎(1)定义：证明一个与正整数n有关的命题，可按下列步骤进行：‎ ‎①证明当n取第一个值n0(n0∈N*)时命题成立，这一步是归纳奠基。‎ ‎②假设n＝k(k≥n0，k∈N*)时命题成立，证明当n＝k＋1时命题也成立，这一步是归纳递推。‎ 完成这两个步骤，就可以断定命题对从n0开始的所有正整数n都成立。‎ ‎(2)框图表示：‎ 微点提醒 ‎1．数学归纳法证题时，不要误把第一个值n0认为是1，如证明多边形内角和定理(n－2)π时，初始值n0＝3。‎ ‎2．数学归纳法证题的关键是第二步，证题时应注意：‎ ‎(1)必须利用归纳假设作基础。‎ ‎(2)证明中可利用综合法、分析法、反证法等方法。‎ ‎(3)解题时要搞清从n＝k到n＝k＋1增加了哪些项或减少了哪些项。‎ 小|题|快|练 一 、走进教材 ‎1．(选修2－2P96B组T1改编)在应用数学归纳法证明凸n边形的对角线为n(n－3)条时，第一步检验n等于(　　)‎ A．1 B．2‎ C．3 D．4‎ ‎【解析】　三角形是边数最少的凸多边形，故第一步应检验n＝3。‎ ‎【答案】　C ‎2．(选修2－2P94例1改编)用数学归纳法证明1＋2＋3＋…＋n2＝，则当n＝k＋1时，左端应在n＝k的基础上加上(　　)‎ A．k2＋1‎ B．(k＋1)2‎ C. D．(k2＋1)＋(k2＋2)＋…＋(k＋1)2‎ ‎【解析】　当n＝k时，左端＝1＋2＋3＋…＋k2。当n＝k＋1时，左端＝1＋2＋3＋…＋k2＋(k2＋1)＋(k2＋2)＋…＋(k＋1)2，故当n＝k＋1时，左端应在n＝k的基础上加上(k2＋1)＋(k2＋2)＋…＋(k＋1)2。故选D。‎ ‎【答案】　D 二、双基查验 ‎1．用数学归纳法证明1＋a＋a2＋…＋an＋1＝(a≠1，n∈N*)，在验证n＝1时，等式左边的项是(　　)‎ A．1 B．1＋a C．1＋a＋a2 D．1＋a＋a2＋a3‎ ‎【答案】　C ‎2．用数学归纳法证明不等式1＋＋＋…＋>(n∈N*)成立，其初始值至少应取(　　)‎ A．7 B．8‎ C．9 D．10‎ ‎【解析】　左边＝1＋＋＋…＋＝＝2－，代入验证可知n的最小值是8。故选B。‎ ‎【答案】　B ‎3．已知f(n)＝＋＋＋…＋，则(　　)‎ A．f(n)中共有n项，当n＝2时，f(2)＝＋ B．f(n)中共有n＋1项，当n＝2时，f(2)＝＋＋ C．f(n)中共有n2－n项，当n＝2时，f(2)＝＋ D．f(n)中共有n2－n＋1项，当n＝2时，f(2)＝＋＋ ‎【答案】　D ‎4．设Sn＝1＋＋＋＋…＋，则Sn＋1－Sn＝________。‎ ‎【解析】　∵Sn＋1＝1＋＋＋＋…＋＋＋…＋，‎ Sn＝1＋＋＋＋…＋，‎ ‎∴Sn＋1－Sn＝＋＋＋…＋。‎ ‎【答案】　＋＋＋…＋ ‎5．已知{an}满足an＋1＝a－nan＋1，n∈N*，且a1＝2，则a2＝________，a3＝________，a4＝________，猜想an＝________。‎ ‎【答案】　3　4　5　n＋1‎ 考点例析　　　　　　　　　　　　　　　‎ 微考点　大课堂 ‎　　　　　　　　 　 　　　　 对点微练 考点一 ‎ 用数学归纳法证明等式 ‎　　【典例1】　求证：12－22＋32－42＋…＋(2n－1)2－(2n)2＝－n(2n＋1)(n∈N*)。‎ ‎【证明】　①当n＝1时，左边＝12－22＝－3，右边＝－3，等式成立。‎ ‎②假设n＝k(k≥1，k∈N*)时，等式成立，即12－22＋32－42＋…＋(2k－1)2－(2k)2＝－k(2k＋1)。‎ 当n＝k＋1时，12－22＋32－42＋…＋(2k－1)2－(2k)2＋(2k＋1)2－(2k＋2)2＝－k(2k＋1)＋(2k＋1)2－(2k＋2)2＝－k(2k＋1)－(4k＋3)＝－(2k2＋5k＋3)＝－(k＋1)[2(k＋1)＋1]，所以n＝k＋1时，等式也成立。由①②得，等式对任何n∈N*都成立。‎ 反思归纳　数学归纳法证明等式的思路和注意点 ‎1．思路：用数学归纳法证明等式问题，要“先看项”，弄清等式两边的构成规律，等式两边各有多少项，初始值n0是多少。‎ ‎2．注意点：由n＝k时等式成立，推出n＝k＋1时等式成立，一要找出等式两边的变化(差异)，明确变形目标；二要充分利用归纳假设，进行合理变形，正确写出证明过程，不利用归纳假设的证明，就不是数学归纳法。‎ ‎【变式训练】　设f(n)＝1＋＋＋…＋(n∈N*)。求证：f(1)＋f(2)＋…＋f(n－1)＝n[f(n)－1](n≥2，n∈N*)。‎ ‎【证明】　(1)当n＝2时，左边＝f(1)＝1，‎ 右边＝2＝1，‎ 左边＝右边，等式成立。‎ ‎(2)假设n＝k(k≥2，k∈N*)时，结论成立，‎ 即f(1)＋f(2)＋…＋f(k－1)＝k[f(k)－1]，‎ 那么，当n＝k＋1时，‎ f(1)＋f(2)＋…＋f(k－1)＋f(k)＝k[f(k)－1]＋f(k)＝(k＋1)f(k)－k＝(k＋1)－k ‎＝(k＋1)f(k＋1)－(k＋1)＝(k＋1)[f(k＋1)－1]，‎ ‎∴当n＝k＋1时结论仍然成立。‎ 由(1)(2)可知，f(1)＋f(2)＋…＋f(n－1)＝n[f(n)－1](n≥2，n∈N*)。‎ 考点二 ‎ 用数学归纳法证明不等式 ‎【典例2】　已知数列{an}，an≥0，a1＝0，a＋an＋1－1＝a，求证：当n∈N*时，an＜an＋1。‎ ‎【证明】　(1)当n＝1时，‎ 因为a2是方程a＋a2－1＝0的正根，‎ 所以a1＜a2。‎ ‎(2)假设当n＝k(k∈N*)时，0≤ak＜ak＋1，‎ 则由a－a＝(a＋ak＋2－1)－(a＋ak＋1－1)‎ ‎＝(ak＋2－ak＋1)(ak＋2＋ak＋1＋1)＞0，‎ 得ak＋1＜ak＋2，即当n＝k＋1时，an＜an＋1也成立。‎ 根据(1)和(2)，可知an＜an＋1对任何n∈N*都成立。‎ 反思归纳　1.当遇到与正整数n有关的不等式证明时，应用其他办法不容易证，则可考虑应用数学归纳法。‎ ‎2．用数学归纳法证明不等式的关键是由n＝k成立，推证n＝k＋1时也成立，证明时用上归纳假设后，可采用分析法、综合法、作差(作商)比较法、放缩法等证明。‎ ‎【变式训练】　用数学归纳法证明：‎ ‎1＋≤1＋＋＋…＋≤＋n (n∈N*)。‎ ‎【证明】　(1)当n＝1时，‎ 左边＝1＋，右边＝＋1，‎ ‎∴≤1＋≤，即命题成立。‎ ‎(2)假设当n＝k (k∈N*)时命题成立，即 ‎1＋≤1＋＋＋…＋≤＋k，‎ 则当n＝k＋1时，‎ ‎1＋＋＋…＋＋＋＋…＋>1＋＋2k·＝1＋。‎ 又1＋＋＋…＋＋＋＋…＋<＋k＋2k·＝＋(k＋1)，‎ 即n＝k＋1时，命题成立。‎ 由(1)(2)可知，命题对所有n∈N*都成立。‎ 考点三 ‎ 归纳—猜想—证明 ‎【典例3】　设a＞0，f(x)＝，令a1＝1，an＋1＝f(an)，n∈N*。‎ ‎(1)写出a2，a3，a4的值，并猜想数列{an}的通项公式；‎ ‎(2)用数学归纳法证明你的结论。‎ ‎【解析】　(1)∵a1＝1，∴a2＝f(a1)＝f(1)＝；‎ a3＝f(a2)＝；a4＝f(a3)＝。‎ 猜想an＝(n∈N*)。‎ ‎(2)证明：①易知，n＝1时，猜想正确。‎ ‎②假设n＝k(k∈N*)时猜想正确，‎ 即ak＝，‎ 则ak＋1＝f(ak)＝＝＝＝。‎ 这说明，n＝k＋1时猜想正确。‎ 由①②知，对于任何n∈N*，都有an＝。‎ ‎【答案】　见解析 反思归纳　“归纳—猜想—证明”的模式，是不完全归纳法与数学归纳法综合应用的解题模式。其一般思路是：通过观察有限个特例，猜想出一般性的结论，然后用数学归纳法证明。这种方法在解决探索性问题、存在性问题或与正整数有关的命题中有着广泛的应用。其关键是归纳、猜想出公式。‎ ‎【变式训练】　将正整数作如下分组：(1)，(2,3)，(4,5,6)，(7,8,9,10)，(11,12,13,14,15)，(16,17,18,19,20,21)，…，分别计算各组包含的正整数的和如下，试猜测S1＋S3＋S5＋…＋S2n－1的结果，并用数学归纳法证明。‎ S1＝1，‎ S2＝2＋3＝5，‎ S3＝4＋5＋6＝15，‎ S4＝7＋8＋9＋10＝34，‎ S5＝11＋12＋13＋14＋15＝65，‎ S6＝16＋17＋18＋19＋20＋21＝111，‎ ‎……‎ ‎【解析】　由题意知，当n＝1时，S1＝1＝14；‎ 当n＝2时，S1＋S3＝16＝24；‎ 当n＝3时，S1＋S3＋S5＝81＝34；‎ 当n＝4时，S1＋S3＋S5＋S7＝256＝44；‎ 猜想：S1＋S3＋S5＋…＋S2n－1＝n4。‎ 下面用数学归纳法证明：‎ ‎(1)当n＝1时，S1＝1＝14，等式成立。‎ ‎(2)假设当n＝k(k∈N*)时等式成立，‎ 即S1＋S3＋S5＋…＋S2k－1＝k4，‎ 那么，当n＝k＋1时，S1＋S3＋S5＋…＋S2k－1＋S2k＋1＝k4＋[(2k2＋k＋1)＋(2k2＋k＋2)＋…＋(2k2＋k＋2k＋1)]＝k4＋(2k＋1)(2k2＋2k＋1)＝k4＋4k3＋6k2＋4k＋1＝(k＋1)4，这就是说，当n＝k＋1时，等式也成立。‎ 根据(1)和(2)，可知对于任意的n∈N*，‎ S1＋S3＋S5＋…＋S2n－1＝n4都成立。‎ ‎【答案】　见解析 考题选萃　　　　　　　　　　　　　　　‎ 微考场　新提升 ‎　　　　　　　　 　 　　　　 随堂自测 ‎　　　　　　　　　　　　　‎ ‎1．用数学归纳法证明2n>2n＋1，n的第一个取值应是(　　)‎ A．1　　　B．‎2　‎　　C．3　　　D．4‎ 解析　∵n＝1时，21＝2,2×1＋1＝3,2n>2n＋1不成立；‎ n＝2时，22＝4,2×2＋1＝5,2n>2n＋1不成立；‎ n＝3时，23＝8,2×3＋1＝7,2n>2n＋1成立。‎ ‎∴n的第一个取值应是3。故选C。‎ 答案　C ‎2．用数学归纳法证明“1＋＋＋＋…＋1)不等式成立，推证n＝k＋1时不等式成立，左边应增加的项数为(　　)‎ A．k B．k＋1 ‎ C．2k D．2k＋1‎ 解析　当n＝k时，不等式左侧是1＋＋＋＋…＋，分母各项依次增加1，故当n＝k＋1时，不等式左侧变为1＋＋＋＋…＋＋＋＋…＋，左边应增加的项数为(2k＋1－1)－(2k－1)＝2k＋1－2k＝2k，故选C。‎ 答案　C ‎3．(2016·承德月考)已知n为正偶数，用数学归纳法证明1－＋－＋…－＝2时，若已假设n＝k(k≥2且k为偶数)时命题为真，则还需要用归纳假设再证(　　)‎ A．n＝k＋1时等式成立 B．n＝k＋2时等式成立 C．n＝2k＋2时等式成立 D．n＝2(k＋2)时等式成立 解析　k为偶数，则k＋2为下一个偶数，故选B。‎ 答案　B ‎4．(2017·潍坊模拟)某个命题与正整数有关，若当n＝k(k∈N*)时该命题成立，那么可推得当n＝k＋1时该命题也成立，现已知当n＝4时该命题不成立，那么可推得(　　)‎ A．当n＝5时，该命题不成立 B．当n＝5时，该命题成立 C．当n＝3时，该命题成立 D．当n＝3时，该命题不成立 解析　由数学归纳法的特点可以知道，当n＝4时该命题不成立，可知当n＝3时，该命题不成立。故选D。‎ 答案　D ‎5．(2016·济宁模拟)在数列{an}中，a1＝，且Sn＝n(2n－1)an，通过求a2，a3，a4，猜想an的表达式为(　　)‎ A．an＝ B．an＝ C．an＝ D．an＝ 解析　由a1＝，Sn＝n(2n－1)an，求得a2＝＝，a3＝＝，a4＝＝。猜想an＝。故选C。‎ 答案　C