四川省成都外国语学校2019-2020学年高一下学期期末考试数学（理）试题 Word版含答案 11页

成都外国语学校 2019~2020学年下期末考试 高一理科数学 ‎ ‎ 一、选择题（共12小题；共60分）‎ ‎1. 计算（ ）‎ A. B. C. D. ‎ ‎ ‎ ‎2. 在等差数列 中，若 ，，则 ）‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎3. 已知直线与平行.则实数的值（ ）‎ A.2 B. C. D. 或2 ‎ ‎ ‎ ‎4. 若，且，则下列不等式中一定正确的是（ ）‎ A. B. C. D. ‎ ‎ ‎ ‎5. 在 中，若 ，则 是 （ ）‎ ‎ A. 直角三角形 B. 等边三角形 ‎ C. 钝角三角形 D. 等腰直角三角形 高一数学理科 第11页（共4页）‎ ‎6. 已知等比数列 的各项都为正数，且 ，， 成等差数列，则 的值是 （ ）‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎7．已知一个正三棱锥的高为3，如下图是其底面用斜二测画法所画出的水平放置的直观图，其中，则此正三棱锥的体积为（ ）‎ A． B． C． D．‎ ‎8．已知直线恒过定点A,点A也在直线上，其中均为正数，则的最小值为（ ） ‎ A．2 B.4 C． 6 D． 8‎ ‎9. 如图，在 中， 是边 上的点，且 ， ，，则 的值为 （ ）‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎10. 满足, 的恰有一个, 那么的取值范围是( )‎ A. B. ‎ C. D. 或 高一数学理科 第11页（共4页）‎ ‎ ‎ ‎11. 如图，圆与轴相切于点，与轴正半轴交于两点（B在A的上方），且．过点任作一条直线与圆相交于两点，的值为（ ）‎ A.2 B. 3 C. 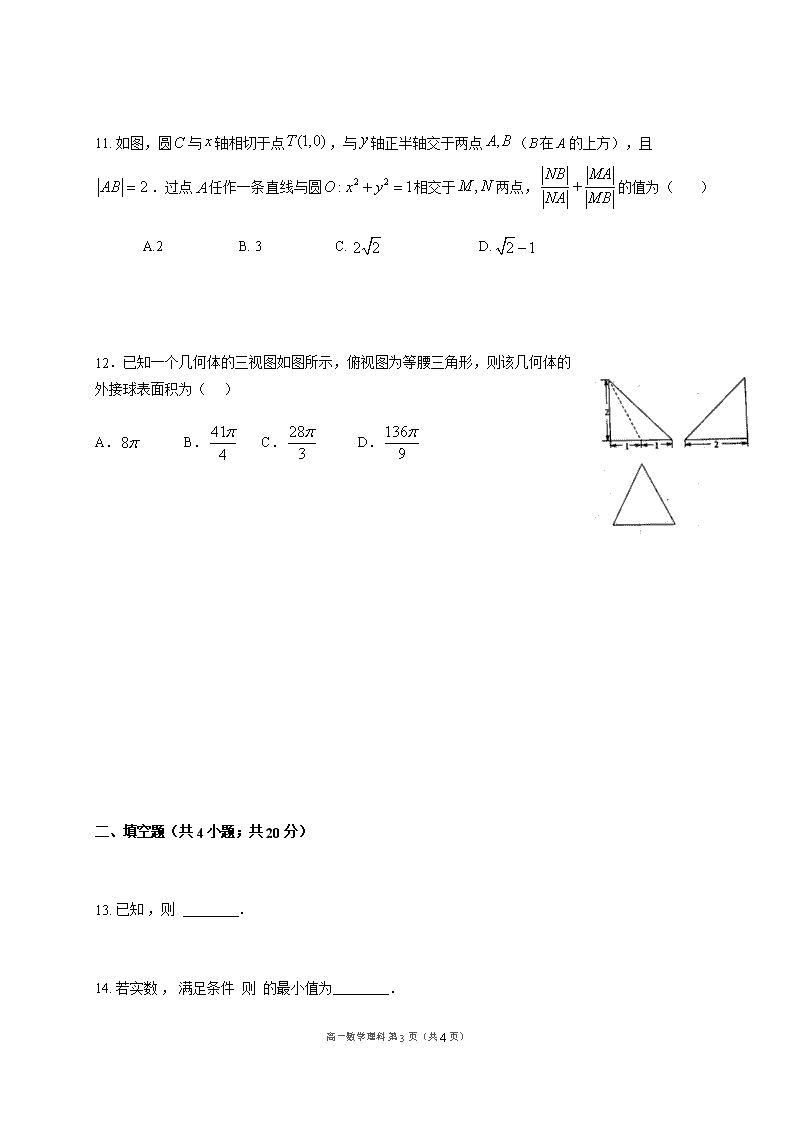D.‎ ‎ ‎ ‎12．已知一个几何体的三视图如图所示，俯视图为等腰三角形，则该几何体的外接球表面积为（ ）‎ A． B． C． D．‎ ‎ ‎ 二、填空题（共4小题；共20分）‎ ‎13. 已知 ，则  ．‎ ‎ ‎ ‎14. 若实数 ， 满足条件 则 的最小值为  ．‎ 高一数学理科 第11页（共4页）‎ ‎ ‎ ‎15. 过点引圆的切线，其中一个切点为，则长度为________.‎ ‎16. 在 中，，， 分别是角 ，， 的对边，且 ，若 ，，‎ 则 的值为  ．‎ ‎ ‎ 三、解答题（共6小题；共78分）‎ ‎17. 已知．‎ ‎（1）求的值；‎ ‎（2）求的值．‎ ‎ ‎ ‎18. 已知函数 ．‎ ‎（1）若 ，求函数 的值域；‎ ‎（2）设 的三个内角 ，， 所对的边分别是 ，，．若 为锐角且 ，，．求 的值．‎ ‎ ‎ 高一数学理科 第11页（共4页）‎ ‎19. 已知关于直线对称，‎ 且圆心在轴上.‎ ‎（1）求的标准方程；‎ ‎（2）已知动点在直线上，过点引的两条切线、，切点分别为.‎ 记四边形的面积为，求的最小值；‎ ‎ ‎ ‎20. 设等差数列 的前 项和为 ，且 ，．‎ ‎（1）求数列 的通项公式；‎ ‎（2）设数列 前 项和为 ，且 ．令 ．‎ 求数列 的前 项和 ．‎ ‎ ‎ 高一数学理科 第11页（共4页）‎ ‎21. 已知中，角，，所对的边分别为，，，，且满足.‎ ‎（1）求的面积；‎ ‎（2）若，求的最大值.‎ ‎ ‎ ‎22. 已知数列满足，‎ ‎（1）求，的值；‎ ‎（2）求证：数列是等比数列，并求的通项公式；‎ ‎（3）设，若不等式对于 任意都成立，求正数的最大值.‎ 高一数学理科 第11页（共4页）‎ 高一数学理科答案 第一部分 ‎1、A 2、B 3、A 4、C 5、B 6、B ‎7、A 8、D 9、D 10、D 11、C 12、B 第二部分 ‎13. ‎ ‎14. 1‎ ‎【解析】根据实数 ， 满足条件 画出可行域，‎ ‎15. ‎ ‎16. 或 ‎ ‎【解析】，‎ 即有 ，‎ 即 ，‎ 即有 ，‎ 由于 为三角形的内角，则 ，‎ 又 ，即有 ，‎ 又 ，‎ 解得，， 或 ，．‎ ‎16. ‎ ‎【解析】设向量 ， 的夹角为 ，，‎ 因为 ，‎ 所以 ．‎ 又 ，则 ，‎ 高一数学理科 第11页（共4页）‎ 所以 恒成立，‎ 因为 ，‎ 所以 ．即 的最小值为 ．‎ 第三部分 ‎17（1）由 所以．‎ 则 ‎（2）因为，．‎ 所以 ‎18. （1） ， .‎ ‎      （2） ，，，，．‎ ‎19. （1）由题意知，‎ 圆心在直线上，即，‎ 又因为圆心在轴上，所以，‎ 由以上两式得：，，‎ 所以.‎ 高一数学理科 第11页（共4页）‎ 故的标准方程为.‎ ‎（2）①如图，的圆心为，半径，‎ 因为、是的两条切线，‎ 所以，，‎ 故 又因为，‎ 根据平面几何知识，要使最小，只要最小即可.‎ 易知，当点坐标为时，‎ ‎.‎ 此时.‎ ‎20. （1） 设等差数列 的首项为 ，公差为 ，‎ 由 ， 得 ‎ ‎ 解得 ，．‎ 因此 ．‎ ‎      （2） 由题意知：．‎ 所以 时，，‎ 故 ，‎ 所以 ，‎ 则 ，‎ 两式相减得 ‎ 高一数学理科 第11页（共4页）‎ ‎ ‎ 整理得 ，‎ 所以数列 的前 项和 ．‎ ‎21解：‎ ‎（1）在中，，∴‎ ‎∵‎ ‎∴‎ ‎∵，∴‎ ‎∴‎ ‎（2）∵‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∴当时，取最大值.‎ ‎22. 解：（1）‎ ‎（2）证明：，‎ 可得an+1+2n＝3（an+2n﹣1），‎ 所以{an+2n﹣1}是以3为首项、3为公比的等比数列，所以an+2n﹣1＝3n，‎ 高一数学理科 第11页（共4页）‎ 则an＝3n﹣2n﹣1，n∈N*；‎ ‎（3）bn＝log （3n﹣2n﹣1+2n﹣1）+1＝log3n+1＝2n+1，‎ 不等式，即•••，‎ 设f（n）•••，‎ ‎•1，‎ 所以f（n+1）＞f（n），即当n增大时，f（n）也增大，‎ 所以只需f（n）min即可．因为f（n）min＝f（1）•，‎ 所以，即k≤4，‎ 所以正数k的最大值为4．‎ 高一数学理科 第11页（共4页）‎