【数学】2021届一轮复习北师大版（理）第八章　第4讲　直线、平面垂直的判定与性质学案 24页

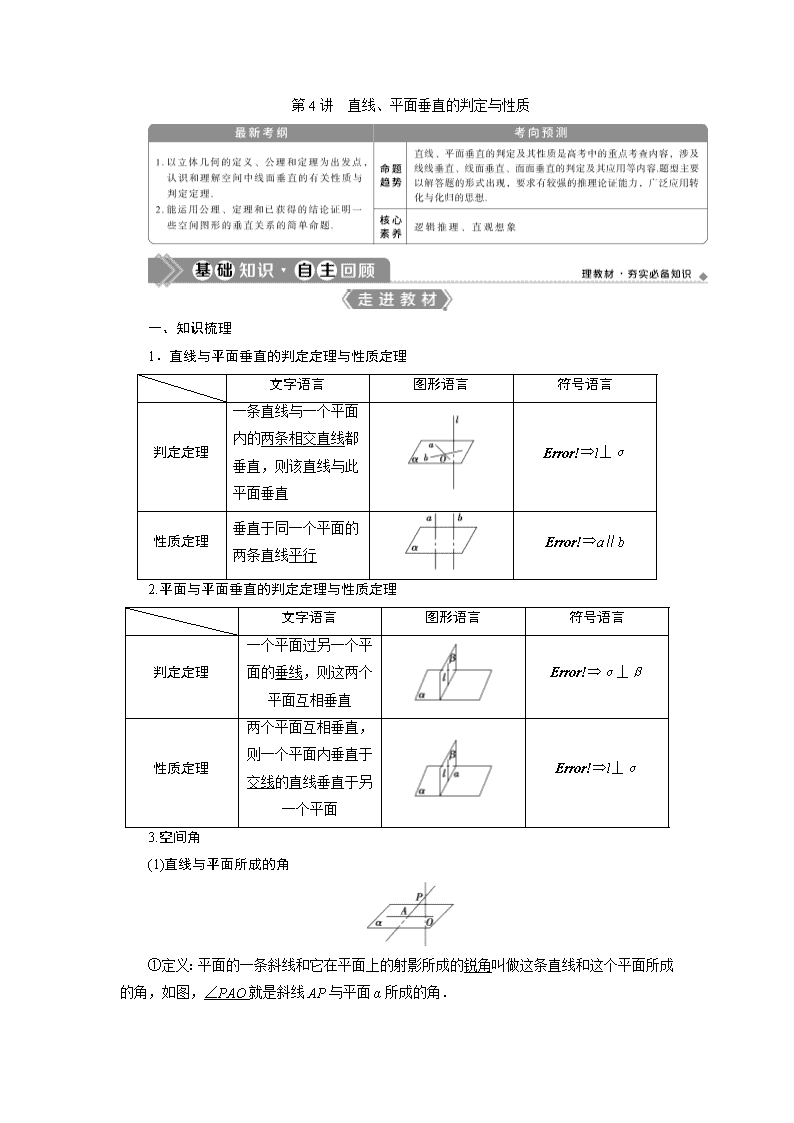
第4讲　直线、平面垂直的判定与性质 一、知识梳理 ‎1．直线与平面垂直的判定定理与性质定理 文字语言 图形语言 符号语言 判定定理 一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直 ⇒l⊥α 性质定理 垂直于同一个平面的两条直线平行 ⇒a∥b ‎2.平面与平面垂直的判定定理与性质定理 文字语言 图形语言 符号语言 判定定理 一个平面过另一个平面的垂线，则这两个平面互相垂直 ⇒α⊥β 性质定理 两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面 ⇒l⊥α ‎3.空间角 ‎(1)直线与平面所成的角 ‎①定义：平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角，如图，∠PAO就是斜线AP与平面α所成的角．‎ ‎②线面角θ的范围：θ∈．‎ ‎(2)二面角 ‎①定义：从一条直线出发的两个半平面所组成的图形叫做二面角．这条直线叫做二面角的棱．两个半平面叫做二面角的面．‎ 如图的二面角，可记作：二面角αlβ或二面角PABQ．‎ ‎②二面角的平面角 如图，过二面角αlβ的棱l上一点O在两个半平面内分别作BO⊥l，AO⊥l，则∠AOB就叫做二面角αlβ的平面角．‎ ‎③二面角的范围 设二面角的平面角为θ，则θ∈[0，π]．‎ ‎④当θ＝时，二面角叫做直二面角．‎ 常用结论 ‎1．线线、线面、面面垂直间的转化 ‎2．两个重要定理 ‎(1)三垂线定理 在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直．‎ ‎(2)三垂线定理的逆定理 在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直．‎ ‎3．重要结论 ‎(1)若两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．‎ ‎(2)若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法)．‎ ‎(3)垂直于同一条直线的两个平面平行．‎ ‎(4)一条直线垂直于两平行平面中的一个，则这一条直线与另一个平面也垂直．‎ 二、教材衍化 ‎1．下列命题中错误的是________(填序号)．‎ ‎①如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β ‎②如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β ‎③如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥平面γ ‎④如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β 解析：对于④，若平面α⊥平面β，则平面α内的直线可能不垂直于平面β，即与平面β的关系还可以是斜交、平行或在平面β内，其他选项均是正确的．‎ 答案：④‎ ‎2．在三棱锥PABC中，点P在平面ABC中的射影为点O.‎ ‎(1)若PA＝PB＝PC，则点O是△ABC的________心；‎ ‎(2)若PA⊥PB，PB⊥PC，PC⊥PA，则点O是△ABC的________心．‎ 解析：(1)如图1，连接OA，OB，OC，OP，‎ 在Rt△POA，Rt△POB和Rt△POC中，PA＝PC＝PB，‎ 所以OA＝OB＝OC，即O为△ABC的外心．‎ ‎　　‎ ‎(2)如图2，延长AO，BO，CO分别交BC，AC，AB于点H，D，G.‎ 因为PC⊥PA，PB⊥PC，PA∩PB＝P，‎ 所以PC⊥平面PAB，又AB平面PAB，所以PC⊥AB，‎ 因为AB⊥PO，PO∩PC＝P，‎ 所以AB⊥平面PGC，又CG平面PGC，‎ 所以AB⊥CG，即CG为△ABC边AB上的高．‎ 同理可证BD，AH分别为△ABC边AC，BC上的高，即O为△ABC的垂心．‎ 答案：(1)外　(2)垂 一、思考辨析 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)直线l与平面α内的无数条直线都垂直，则l⊥α.(　　)‎ ‎(2)垂直于同一个平面的两平面平行．(　　)‎ ‎(3)直线a⊥α，b⊥α，则a∥b.(　　)‎ ‎(4)若α⊥β，a⊥β，则a∥α.(　　)‎ ‎(5)若直线a⊥平面α，直线b∥α，则直线a与b垂直．(　　)‎ ‎(6)若平面α内的一条直线垂直于平面β内的无数条直线，则α⊥β.(　　)‎ 答案：(1)×　(2)×　(3)√　(4)×　(5)√　(6)×‎ 二、易错纠偏 (1)忽略线面垂直的条件致误；‎ ‎(2)忽视平面到空间的变化致误．‎ ‎1．“直线a与平面α内的无数条直线都垂直”是“直线a与平面α垂直”的________条件．‎ 解析：根据直线与平面垂直的定义知“直线a与平面α内的无数条直线都垂直”不能推出“直线a与平面α垂直”，反之则可以，所以应是必要不充分条件．‎ 答案：必要不充分 ‎2．已知直线a，b，c，若a⊥b，b⊥c，则a与c的位置关系为________．‎ 解析：若a，b，c在同一个平面内，由题设条件可得a∥c；若在空间中，则直线a与c的位置关系不确定，平行，相交，异面都有可能．‎ 答案：平行，相交或异面 ‎　　　　　　线面垂直的判定与性质(多维探究)‎ 角度一　线面垂直的证明 ‎ 如图 所示，在四棱锥PABCD中，AB⊥平面PAD，AB∥CD，PD＝AD，E是PB的中点，F是DC上的点，且DF＝AB，PH为△PAD中AD边上的高．‎ 求证：(1)PH⊥平面ABCD；‎ ‎(2)EF⊥平面PAB.‎ ‎【证明】　(1)因为AB⊥平面PAD，PH平面PAD，所以PH⊥AB.‎ 因为PH为△PAD中AD边上的高，所以PH⊥AD.‎ 因为AB∩AD＝A，AB平面ABCD，AD平面ABCD，所以PH⊥平面ABCD.‎ ‎(2)如图，取PA的中点M，连接MD，ME.因为E是PB的中点，所以ME綊AB.‎ 又因为DF綊AB.‎ 所以ME綊DF，‎ 所以四边形MEFD是平行四边形，‎ 所以EF∥MD.‎ 因为PD＝AD，所以MD⊥PA.‎ 因为AB⊥平面PAD，所以MD⊥AB.‎ 因为PA∩AB＝A，所以MD⊥平面PAB，‎ 所以EF⊥平面PAB.‎ 角度二　线面垂直性质的应用 ‎ 如图，在三棱锥ABCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，F(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD.‎ 求证：(1)EF∥平面ABC；‎ ‎(2)AD⊥AC.‎ ‎【证明】　(1)在平面ABD内，因为AB⊥AD，EF⊥AD，所以EF∥AB.‎ 又因为EF平面ABC，AB平面ABC，‎ 所以EF∥平面ABC.‎ ‎(2)因为平面ABD⊥平面BCD，‎ 平面ABD∩平面BCD＝BD，‎ BC平面BCD，BC⊥BD，‎ 所以BC⊥平面ABD.‎ 因为AD平面ABD，‎ 所以BC⊥AD.‎ 又AB⊥AD，BC∩AB＝B，AB平面ABC，BC平面ABC，‎ 所以AD⊥平面ABC.‎ 又因为AC平面ABC，‎ 所以AD⊥AC.‎ ‎(1)判定线面垂直的四种方法 ‎(2)判定线线垂直的四种方法 ‎　 ‎ ‎　‎ 如图所示，在四棱锥 PABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．‎ 证明：(1)CD⊥AE；‎ ‎(2)PD⊥平面ABE.‎ 证明：(1)在四棱锥PABCD中，‎ 因为PA⊥底面ABCD，CD平面ABCD，‎ 所以PA⊥CD.因为AC⊥CD，PA∩AC＝A，‎ 所以CD⊥平面PAC.‎ 而AE平面PAC，所以CD⊥AE.‎ ‎(2)由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.‎ 因为E是PC的中点，所以AE⊥PC.‎ 由(1)知AE⊥CD，且PC∩CD＝C，‎ 所以AE⊥平面PCD.‎ 而PD平面PCD，‎ 所以AE⊥PD.‎ 因为PA⊥底面ABCD，所以PA⊥AB.‎ 又因为AB⊥AD且PA∩AD＝A，‎ 所以AB⊥平面PAD，而PD⊂平面PAD，‎ 所以AB⊥PD.又因为AB∩AE＝A，‎ 所以PD⊥平面ABE.‎ ‎　　　　　　面面垂直的判定与性质(典例迁移)‎ ‎ (一题多解)如图，四棱锥PABCD中，AB⊥AC，AB⊥PA，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．‎ ‎(1)求证：CE∥平面PAD；‎ ‎(2)求证：平面EFG⊥平面EMN.‎ ‎【证明】　(1)法一：取PA的中点H，连接EH，DH.‎ 又E为PB的中点，‎ 所以EH綊AB.‎ 又CD綊AB，‎ 所以EH綊CD.‎ 所以四边形DCEH是平行四边形，‎ 所以CE∥DH.‎ 又DH平面PAD，CE平面PAD.‎ 所以CE∥平面PAD.‎ 法二：连接CF.因为F为AB的中点，所以AF＝AB.‎ 又CD＝AB，‎ 所以AF＝CD.‎ 又AF∥CD，所以四边形AFCD为平行四边形．‎ 因此CF∥AD.‎ 又CF平面PAD，AD平面PAD，‎ 所以CF∥平面PAD.‎ 因为E，F分别为PB，AB的中点，所以EF∥PA.‎ 又EF平面PAD，PA平面PAD，‎ 所以EF∥平面PAD.‎ 又因为CF∩EF＝F.故平面CEF∥平面PAD.‎ 又因为CE平面CEF，‎ 所以CE∥平面PAD.‎ ‎(2)因为E，F分别为PB，AB的中点，‎ 所以EF∥PA，又AB⊥PA，所以AB⊥EF.‎ 同理可得AB⊥FG.‎ 又EF∩FG＝F，EF⊂平面EFG，‎ FG平面EFG，‎ 因此AB⊥平面EFG.‎ 又M，N分别为PD，PC的中点，所以MN∥CD.‎ 又AB∥CD，所以MN∥AB，所以MN⊥平面EFG.‎ 又MN平面EMN，‎ 所以平面EFG⊥平面EMN.‎ ‎【迁移探究1】　(变问法)在本例条件下，证明：平面EMN⊥平面PAC.‎ 证明：因为AB⊥PA，AB⊥AC，且PA∩AC＝A，‎ 所以AB⊥平面PAC.‎ 又MN∥CD，CD∥AB，所以MN∥AB.‎ 所以MN⊥平面PAC.‎ 又MN平面EMN，‎ 所以平面EMN⊥平面PAC.‎ ‎【迁移探究2】　(变问法)在本例条件下，证明：平面EFG∥平面PAC.‎ 证明：因为E，F，G分别为PB，AB，BC的中点，‎ 所以EF∥PA，FG∥AC，‎ 又EF平面PAC，PA平面PAC，‎ 所以EF∥平面PAC.‎ 同理，FG∥平面PAC.‎ 又EF∩FG＝F，所以平面EFG∥平面PAC.‎ 证明面面垂直的两种常用方法 ‎(1)用面面垂直的判定定理，即先证明其中一个平面经过另一个平面的一条垂线．‎ ‎(2)用面面垂直的定义，即证明两个平面所成的二面角是直二面角，把证明面面垂直的问题转化为证明平面角为直角的问题．　 ‎ ‎　如图，在四棱锥PABCD中，底面ABCD为矩形，平面PAD⊥平面ABCD，PA⊥PD，PA＝PD，E，F分别为AD，PB的中点．‎ ‎(1)求证：PE⊥BC；‎ ‎(2)求证：平面PAB⊥平面PCD；‎ ‎(3)求证：EF∥平面PCD.‎ 证明：(1)因为PA＝PD，E为AD的中点，‎ 所以PE⊥AD.因为底面ABCD为矩形，所以BC∥AD.‎ 所以PE⊥BC.‎ ‎(2)因为底面ABCD为矩形，所以AB⊥AD.又因为平面PAD⊥平面ABCD，所以AB⊥平面PAD.所以AB⊥PD.又因为PA⊥PD，所以PD⊥平面PAB.所以平面PAB⊥平面PCD.‎ ‎(3)取PC的中点G，连接FG，DG.‎ 因为F，G分别为PB，PC的中点，‎ 所以FG∥BC，FG＝BC.‎ 因为四边形ABCD为矩形，且E为AD的中点，‎ 所以DE∥BC，DE＝BC.‎ 所以DE∥FG，DE＝FG.‎ 所以四边形DEFG为平行四边形．‎ 所以EF∥DG.‎ 又因为EF平面PCD，DG平面PCD，‎ 所以EF∥平面PCD.‎ ‎　　　　　　垂直关系中的探索性问题(师生共研)‎ ‎ 如图，在三棱柱ABCA1B1C1中，侧棱AA1⊥底面ABC，M为棱AC的中点．AB＝BC，AC＝2，AA1＝.‎ ‎(1)求证：B1C∥平面A1BM；‎ ‎(2)求证：AC1⊥平面A1BM；‎ ‎(3)在棱BB1上是否存在点N，使得平面AC1N⊥平面AA1C1C？如果存在，求此时的值；如果不存在，请说明理由．‎ ‎【解】　(1)证明：连接AB1与A1B，两线交于点O，连接OM.‎ 在△B1AC中，因为M，O分别为AC，AB1的中点，‎ 所以OM∥B1C，‎ 又因为OM平面A1BM，B1C平面A1BM，‎ 所以B1C∥平面A1BM.‎ ‎(2)证明：因为侧棱AA1⊥底面ABC ，BM平面ABC，‎ 所以AA1⊥BM，‎ 又因为M为棱AC的中点，AB＝BC，所以BM⊥AC.‎ 因为AA1∩AC＝A，AA1，AC平面ACC1A1，‎ 所以BM⊥平面ACC1A1，‎ 所以BM⊥AC1.‎ 因为AC＝2，所以AM＝1.‎ 又因为AA1＝，所以在Rt△ACC1和Rt△A1AM中，‎ tan∠AC1C＝tan∠A1MA＝，‎ 所以∠AC1C＝∠A1MA，‎ 即∠AC1C＋∠C1AC＝∠A1MA＋∠C1AC＝90°，‎ 所以A1M⊥AC1.‎ 因为BM∩A1M＝M，BM，A1M平面A1BM，‎ 所以AC1⊥平面A1BM.‎ ‎(3)‎ 当点N为BB1的中点，即＝时，‎ 平面AC1N⊥平面AA1C1C.‎ 证明如下：‎ 设AC1的中点为D，连接DM，DN.因为D，M分别为AC1，AC的中点，‎ 所以DM∥CC1，且DM＝CC1.‎ 又因为N为BB1的中点，所以DM∥BN，且DM＝BN，‎ 所以四边形BNDM为平行四边形，‎ 所以BM∥DN，‎ 因为BM⊥平面ACC1A1，所以DN⊥平面AA1C1C.‎ 又因为DN平面AC1N，‎ 所以平面AC1N⊥平面AA1C1C.‎ ‎(1)对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论则否定假设．‎ ‎(2)对于探索性问题用向量法比较容易入手．一般先假设存在，设出空间点的坐标，转化为代数方程是否有解的问题，若有解且满足题意则存在，若有解但不满足题意或无解则不存在．　 ‎ ‎　如图所示，平面ABCD⊥平面BCE，四边形ABCD为矩形，BC＝CE，点F为CE的中点．‎ ‎(1)证明：AE∥平面BDF；‎ ‎(2)点M为CD上任意一点，在线段AE上是否存在点P，使得PM⊥BE? 若存在，确定点P的位置，并加以证明；若不存在，请说明理由．‎ 解：(1)证明：连接AC交BD于点O，连接OF.‎ 因为四边形ABCD是矩形，‎ 所以O为AC的中点．‎ 又F为EC的中点，所以OF∥AE.‎ 又OF平面BDF，‎ AE平面BDF，‎ 所以AE∥平面BDF.‎ ‎(2)当点P为AE的中点时，‎ 有PM⊥BE，证明如下：‎ ‎ ‎ 取BE的中点H，连接DP，PH，CH.‎ 因为P为AE的中点，H为BE的中点，所以PH∥AB.‎ 又AB∥CD，所以PH∥CD，‎ 所以P，H，C，D四点共面．‎ 因为平面ABCD⊥平面BCE，且平面ABCD∩平面BCE＝BC，CD⊥BC，‎ CD平面ABCD，所以CD⊥平面BCE.‎ 又BE平面BCE，所以CD⊥BE，‎ 因为BC＝CE，且H为BE的中点，‎ 所以CH⊥BE.‎ 又CH∩CD＝C，且CH，CD平面DPHC，‎ 所以BE⊥平面DPHC.‎ 又PM平面DPHC，所以PM⊥BE.‎ ‎　逻辑推理平面图形折叠问题的解题技巧 一、将平面图形折叠成立体图形 ‎　如图是一个正方体表面的一种展开图，图中的四条线段AB，CD，EF和GH在原正方体中相互异面的有________对．‎ ‎【解析】　平面图形的折叠应注意折前折后各元素相对位置的变化．画出图形即可判断，相互异面的线段有AB与CD，EF与GH，AB与GH，共3对．‎ ‎【答案】　3‎ 画折叠图形一般以某个面为基础，依次将其余各面翻折还原，当然，‎ 画图之前要对翻折后形成的立体图形有所认识，这是解答此类问题的关键．‎ ‎　 ‎ 二、折叠中的“变”与“不变”‎ ‎　如图①，在等腰直角三角形ABC中，∠A＝90°，BC＝6，D，E分别是AC，AB上的点，CD＝BE＝，O为BC的中点．将△ADE沿DE折起，得到如图②所示的四棱锥A′－BCDE，其中A′O＝.‎ ‎(1)证明：A′O⊥平面BCDE；‎ ‎(2)求二面角A′－CD－B的平面角的余弦值．‎ ‎【解】　(1)证明：在题图①中，易得OC＝3，AC＝3，AD＝2.‎ 连接OD，OE，在△OCD中，由余弦定理可得 OD＝＝.‎ 由翻折不变性可知A′D＝2，‎ 所以A′O2＋OD2＝A′D2，所以A′O⊥OD，‎ 同理可证A′O⊥OE，又OD∩OE＝O，‎ 所以A′O⊥平面BCDE.‎ ‎(2)过O作OH⊥CD交CD的延长线于H，连接A′H，因为A′O⊥平面BCDE，所以A′H⊥CD，所以∠A′HO为二面角A′－CD－B的平面角．‎ 结合题图①可知，H为AC的中点，故OH＝，从而A′H＝＝，所以cos∠A′HO＝＝，‎ 所以二面角A′－CD－B的平面角的余弦值为.‎ 折叠问题的关键有二：①画好两个图——折叠前的平面图和折叠后的立体图；②分析好两个关系——折叠前后哪些位置关系和数量关系发生了变化，哪些没有改变．一般地，在同一半平面内的几何元素之间的关系是不变的．涉及两个半平面内的几何元素之间的关系是要变化的．分别位于两个半平面内但垂直于折叠棱的直线翻折后仍然垂直于折叠棱．‎ ‎　 ‎ 三、立体图形的表面展开图的应用 ‎　在一个底面直径是5 cm，高为2π cm的圆柱形玻璃杯子的上沿B处有一只苍蝇，而恰好在相对的底沿A处有一只蜘蛛，蜘蛛要想用最快的速度捕捉到这只苍蝇，蜘蛛所走的最短的路程是________．‎ ‎【解析】　利用侧面展开图，如图，蜘蛛所走的最短的路程是线段AB的长，AC＝×2π×＝π cm，BC＝2π cm，则AB＝＝π cm，即蜘蛛所走的最短的路程是π cm.‎ ‎【答案】　π cm 求从一点出发沿几何体表面到另一点的最短距离问题：通常把几何体的侧面展开，转化为平面图形中的距离问题．　 ‎ ‎ [基础题组练]‎ ‎1．(2020·辽宁大连模拟)已知直线l和平面α，β，且lα，则“l⊥β”是“α⊥β”的(　　)‎ A．充分不必要条件　　　 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 解析：选A.由面面垂直的判定定理可得，若lα，l⊥β，则α⊥β，充分性成立；若lα，α⊥β，则l与β平行或相交或垂直，必要性不成立．所以若lα，则“l⊥β”是“α⊥β”的充分不必要条件，故选A.‎ ‎2．(2020·河北唐山模拟)如图，在以下四个正方体中，直线AB与平面CDE垂直的是(　　)‎ A．①② B．②④‎ C．①③ D．②③‎ 解析：选B.对于①，易证AB与CE所成角为45°，则直线AB与平面CDE不垂直；对于②，易证AB⊥CE，AB⊥ED，且CE∩ED＝E，则AB⊥平面CDE；对于③，易证AB 与CE所成角为60°，则直线AB与平面CDE不垂直；对于④，易证ED⊥平面ABC，则ED⊥AB，同理EC⊥AB，可得AB⊥平面CDE.故选B.‎ ‎3.(2020·黑龙江鹤岗模拟)如图，在三棱锥V－ABC中，VO⊥平面ABC，O∈CD，VA＝VB，AD＝BD，则下列结论中不一定成立的是(　　)‎ A．AC＝BC ‎ B．AB⊥VC C．VC⊥VD ‎ D．S△VCD·AB＝S△ABC·VO 解析：选C.因为VO⊥平面ABC，AB平面ABC，所以VO⊥AB.因为VA＝VB，AD＝BD，所以VD⊥AB.又因为VO∩VD＝V，所以AB⊥平面VCD.又因为CD平面VCD，所以AB⊥CD.又因为AD＝BD，所以AC＝BC，故A正确．‎ 又因为VC平面VCD，所以AB⊥VC，故B正确；‎ 因为S△VCD＝VO·CD，S△ABC＝AB·CD，所以S△VCD·AB＝S△ABC·VO，故D正确．由题中条件无法判断VC⊥VD.故选C.‎ ‎4.如图，在斜三棱柱ABCA1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在(　　)‎ A．直线AB上 ‎ B．直线BC上 C．直线AC上 ‎ D．△ABC内部 解析：选A.由AC⊥AB，AC⊥BC1，得AC⊥平面ABC1.‎ 因为AC平面ABC，‎ 所以平面ABC1⊥平面ABC.‎ 所以C1在平面ABC上的射影H必在两平面的交线AB上．‎ ‎5.如图，在正四面体PABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论不成立的是(　　)‎ A．BC∥平面PDF B．DF⊥平面PAE C．平面PDF⊥平面PAE D．平面PDE⊥平面ABC 解析：选D.因为BC∥DF，DF平面PDF，‎ BC平面PDF，‎ 所以BC∥平面PDF，故选项A正确；‎ 在正四面体中，AE⊥BC，PE⊥BC，AE∩PE＝E，‎ 且AE，PE平面PAE，‎ 所以BC⊥平面PAE，‎ 因为DF∥BC，所以DF⊥平面PAE，‎ 又DF平面PDF，‎ 从而平面PDF⊥平面PAE.‎ 因此选项B，C均正确．‎ ‎6.如图，在△ABC中，∠ACB＝90°，AB＝8，∠ABC＝60°，PC⊥平面ABC，PC＝4，M是边AB上的一个动点，则PM的最小值为________．‎ 解析：作CH⊥AB于H，连接PH.因为PC⊥平面ABC，所以PH⊥AB，PH为PM的最小值，等于2.‎ 答案：2 ‎7.如图所示，在四棱锥PABCD中，PA⊥底面ABCD，且底面各边都相等，M是边PC上的一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)‎ 解析：‎ 连接AC，BD，则AC⊥BD，因为PA⊥底面ABCD，所以PA⊥BD.又PA∩AC＝A，所以BD⊥平面PAC，所以BD⊥PC.所以当DM⊥PC(或BM⊥PC)时，即有PC⊥平面MBD.‎ 而PC平面PCD，所以平面MBD⊥平面PCD.‎ 答案：DM⊥PC(或BM⊥PC)‎ ‎8.如图，PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，AE⊥PC，AF⊥PB，给出下列结论：①AE⊥BC；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC，其中正确结论的序号是________．‎ 解析：①AE平面PAC，BC⊥AC，BC⊥PA⇒AE⊥BC，故①正确；②AE⊥PC，AE⊥BC，PB平面PBC⇒AE⊥PB，AF⊥PB，EF平面AEF⇒EF⊥PB，故②正确；③若AF⊥BC⇒AF⊥平面PBC，则AF∥AE与已知矛盾，故③错误；由①可知④正确．‎ 答案：①②④‎ ‎9.如图，在多面体ABCDPE中，四边形ABCD和CDPE都是直角梯形，AB∥DC，PE∥DC，AD⊥DC，PD⊥平面ABCD，AB＝PD＝DA＝2PE，CD＝3PE，F是CE的中点．‎ ‎(1)求证：BF∥平面ADP；‎ ‎(2)已知O是BD的中点，求证：BD⊥平面AOF.‎ 证明：‎ ‎(1)如图，取PD的中点为G，连接FG，AG，‎ 因为F是CE的中点，所以FG是梯形CDPE的中位线，‎ 因为CD＝3PE，所以FG＝2PE，‎ FG∥CD，因为CD∥AB，AB＝2PE，‎ 所以AB∥FG，AB＝FG，‎ 即四边形ABFG是平行四边形，‎ 所以BF∥AG，‎ 又BF平面ADP，AG平面ADP，‎ 所以BF∥平面ADP.‎ ‎(2)延长AO交CD于点M，连接BM，FM，‎ 因为BA⊥AD，CD⊥DA，AB＝AD，O为BD的中点，‎ 所以ABMD是正方形，则BD⊥AM，MD＝2PE.‎ 所以FM∥PD，因为PD⊥平面ABCD，‎ 所以FM⊥平面ABCD，所以FM⊥BD，‎ 因为AM∩FM＝M，所以BD⊥平面AMF，‎ 所以BD⊥平面AOF.‎ ‎10．(一题多解)如图1，在等腰梯形PDCB中，PB∥DC，PB＝3，DC＝1，∠DPB＝45°，DA⊥PB于点A，将△PAD沿AD折起，构成如图2所示的四棱锥PABCD，点M在棱PB上，且PM＝MB.‎ ‎(1)求证：PD∥平面MAC；‎ ‎(2)若平面PAD⊥平面ABCD，求点A到平面PBC的距离．‎ 解：(1)证明：在四棱锥PABCD中，连接BD交AC于点N，连接MN，‎ 依题意知AB∥CD，‎ 所以△ABN∽△CDN，‎ 所以＝＝2，‎ 因为PM＝MB，‎ 所以＝＝2，‎ 所以在△BPD中，MN∥PD，‎ 又PD平面MAC，MN平面MAC.‎ 所以PD∥平面MAC.‎ ‎(2)法一：因为平面PAD⊥平面ABCD，且两平面相交于AD，PA⊥AD，PA平面PAD，‎ 所以PA⊥平面ABCD，‎ 所以VPABC＝S△ABC·PA＝××1＝.‎ 因为AB＝2，AC＝＝，‎ 所以PB＝＝，PC＝＝，BC＝＝，‎ 所以PB2＝PC2＋BC2，故∠PCB＝90°，‎ 记点A到平面PBC的距离为h，‎ 所以VAPBC＝S△PBC·h＝×h ‎＝h.‎ 因为VPABC＝VAPBC，‎ 所以＝h，解得h＝.‎ 故点A到平面PBC的距离为.‎ 法二：‎ 因为平面PAD⊥平面ABCD，且两平面相交于AD，PA⊥AD，PA平面PAD，‎ 所以PA⊥平面ABCD，‎ 因为BC平面ABCD，‎ 所以PA⊥BC，‎ 因为AB＝2，AC＝＝，‎ BC＝＝，‎ 所以∠ACB＝90°，即BC⊥AC，‎ 又PA∩AC＝A，PA，AC平面PAC，‎ 所以BC⊥平面PAC，‎ 过点A作AE⊥PC于点E，则BC⊥AE，‎ 因为PC∩BC＝C，PC，BC平面PBC，‎ 所以AE⊥平面PBC，‎ 所以点A到平面PBC的距离为AE＝＝＝.‎ ‎[综合题组练]‎ ‎1.如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE是△ADE绕DE旋转过程中的一个图形，则下列命题中正确的是(　　)‎ ‎①动点A′在平面ABC上的射影在线段AF上；‎ ‎②BC∥平面A′DE；‎ ‎③三棱锥A′FED的体积有最大值．‎ A．①　　　　　　　　　 B．①②‎ C．①②③ D．②③‎ 解析：选C.①中由已知可得平面A′FG⊥平面ABC，‎ 所以点A′在平面ABC上的射影在线段AF上．‎ ‎②BC∥DE，根据线面平行的判定定理可得BC∥平面A′DE.‎ ‎③当平面A′DE⊥平面ABC时，三棱锥A′FED的体积达到最大，故选C.‎ ‎2.如图，梯形ABCD中，AD∥BC，∠ABC＝90°，AD∶BC∶AB＝2∶3∶4，E，F分别是AB，CD的中点，将四边形ADFE沿直线EF进行翻折，给出下列四个结论：①DF⊥BC；②BD⊥FC；③平面BDF⊥平面BCF；④平面DCF⊥平面BCF，则上述结论可能正确的是(　　)‎ A．①③ B．②③‎ C．②④ D．③④‎ 解析：选B.对于①，因为BC∥AD，AD与DF相交但不垂直，所以BC与DF不垂直，则①不成立；对于②，设点D在平面BCF上的射影为点P，当BP⊥CF时就有BD⊥FC，而AD∶BC∶AB＝2∶‎ ‎3∶4可使条件满足，所以②正确；对于③，当点D在平面BCF上的射影P落在BF上时，DP平面BDF，从而平面BDF⊥平面BCF，所以③正确；对于④，因为点D在平面BCF上的射影不可能在FC上，所以④不成立．‎ ‎3．在矩形ABCD中，AB＜BC，现将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折的过程中，给出下列结论：‎ ‎①存在某个位置，使得直线AC与直线BD垂直；‎ ‎②存在某个位置，使得直线AB与直线CD垂直；‎ ‎③存在某个位置，使得直线AD与直线BC垂直．‎ 其中正确结论的序号是________．(写出所有正确结论的序号)‎ 解析：①假设AC与BD垂直，过点A作AE⊥BD于点E，连接CE.则⇒BD⊥平面AEC⇒BD⊥CE，而在平面BCD中，EC与BD不垂直，故假设不成立，①错．‎ ‎②假设AB⊥CD，因为AB⊥AD，所以AB⊥平面ACD，所以AB⊥AC，由AB＜BC可知，存在这样的等腰直角三角形，使AB⊥CD，故假设成立，②正确．‎ ‎③假设AD⊥BC，‎ 因为DC⊥BC，所以BC⊥平面ADC，‎ 所以BC⊥AC，即△ABC为直角三角形，且AB为斜边，而AB＜BC，故矛盾，假设不成立，③错．综上，填②.‎ 答案：②‎ ‎4．如图，直三棱柱ABCA1B1C1中，侧棱长为2，AC＝BC＝1，∠ACB＝90°，D是A1B1的中点，F是BB1上的动点，AB1，DF交于点E.要使AB1⊥平面C1DF，则线段B1F的长为________．‎ 解析：设B1F＝x，因为AB1⊥平面C1DF，DF平面C1DF，所以AB1⊥DF.‎ 由已知可以得A1B1＝，‎ 设Rt△AA1B1斜边AB1上的高为h，则DE＝h，‎ 又2×＝h×，‎ 所以h＝，DE＝.‎ 在Rt△DB1E中，B1E＝＝.‎ 由面积相等得× ＝x，得x＝.即线段B1F的长为.‎ 答案： ‎5．(2020·河南郑州第二次质量预测)如图，四棱锥P－ABCD中，底面ABCD 是边长为2的菱形，∠BAD＝，△PAD是等边三角形，F为AD的中点，PD⊥BF.‎ ‎(1)求证：AD⊥PB；‎ ‎(2)若E在线段BC上，且EC＝BC，能否在棱PC上找到一点G，使平面DEG⊥平面ABCD？若存在，求出三棱锥D－CEG的体积；若不存在，请说明理由．‎ 解：(1)证明：连接PF，因为△PAD是等边三角形，F是AD的中点，所以PF⊥AD.‎ 因为底面ABCD是菱形，∠BAD＝，所以BF⊥AD.‎ 又PF∩BF＝F，所以AD⊥平面BFP，又PB平面BFP，‎ 所以AD⊥PB.‎ ‎(2)能在棱PC上找到一点G，使平面DEG⊥平面ABCD.‎ 由(1)知AD⊥BF，因为PD⊥BF，AD∩PD＝D，所以BF⊥平面PAD.‎ 又BF平面ABCD，所以平面ABCD⊥平面PAD，‎ 又平面ABCD∩平面PAD＝AD，且PF⊥AD，所以PF⊥平面ABCD.‎ 连接CF交DE于点H，过H作HG∥PF交PC于点G，所以GH⊥平面ABCD.‎ 又GH平面DEG，所以平面DEG⊥平面ABCD.‎ 因为AD∥BC，所以△DFH∽△ECH，所以＝＝，‎ 所以＝＝，‎ 所以GH＝PF＝，‎ 所以VD－CEG＝VG－CDE＝S△CDE·GH＝×DC·CE·sin ·GH＝.‎ ‎6．如图(1)，在Rt△ABC中，∠ABC＝90°，D为AC的中点，AE⊥BD于点E(不同于点D)，延长AE交BC于点F，将△ABD沿BD折起，得到三棱锥A1BCD，如图(2)所示．‎ ‎(1)若M是FC的中点，求证：直线DM∥平面A1EF；‎ ‎(2)求证：BD⊥A1F；‎ ‎(3)若平面A1BD⊥平面BCD，试判断直线A1B与直线CD能否垂直？并说明理由．‎ 解：(1)证明：因为D，M分别为AC，FC的中点，‎ 所以DM∥EF，‎ 又EF平面A1EF，DM平面A1EF，‎ 所以DM∥平面A1EF.‎ ‎(2)证明：因为A1E⊥BD，EF⊥BD且A1E∩EF＝E，‎ 所以BD⊥平面A1EF.‎ 又A1F平面A1EF，‎ 所以BD⊥A1F.‎ ‎(3)直线A1B与直线CD不能垂直．理由如下：‎ 因为平面A1BD⊥平面BCD，平面A1BD∩平面BCD＝BD，EF⊥BD，EF⊂平面BCD，‎ 所以EF⊥平面A1BD.‎ 因为A1B平面A1BD，‎ 所以A1B⊥EF，‎ 又因为EF∥DM，所以A1B⊥DM.‎ 假设A1B⊥CD，‎ 因为CD∩DM＝D，‎ 所以A1B⊥平面BCD，‎ 所以A1B⊥BD，‎ 这与∠A1BD为锐角矛盾，‎ 所以直线A1B与直线CD不能垂直．‎