江西省吉安市2013届高三第一次模拟考试 数学理 9页

‎2013届高三模拟试卷 数学（理）试卷 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页， 满分150分，考试时间120分钟．‎ 考生注意：‎ ‎1. 答题前，考生务必将自己的准考证号、姓名填写在答题卡上，考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致．‎ ‎2. 第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．第Ⅱ卷用0.5毫米的黑色墨水签字笔在答题卡上作答．若在试题卷上作答，答案无效．‎ ‎3. 考试结束，监考员将试题卷、答题卡一并收回．‎ 第Ⅰ卷 一、选择题：（本大题共10小题，每小题5分，共50分，每题只有一个正确答案） ‎ ‎1．已知i是虚数单位，则在复平面内对应的点位于 ‎ A．第一象限 B.第二象限 C.第三象限 D.第四象限 ‎2．执行如图所示的程序框图，若输入x==2，则输出y的值为 A. 5 B. 9 C. 14 D. 41‎ ‎3．设，则是 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎4．已知是双曲线的两个焦点，Q是双曲线上任一点（不是顶点），从某一焦点引的平分线的垂线，垂足为P，则点P的轨迹是 ‎ A. 直线 B. 圆 C. 椭圆 D. 双曲线 ‎5．已知函数对定义域内的任意都有=，且当时其导函数满足若则 ‎ A． B．‎ ‎ C． D．‎ ‎6．一组数据共有7个数，记得其中有10,2,5,2,4,2，还有一个数没记清，但知道这组数的平均数、中位数、众数依次成等比数列，这个数的所有可能值的和为 侧视图 正视图 俯视图 ‎1‎ ‎3‎ ‎2‎ 侧视图 正视图 俯视图 ‎2‎ ‎3‎ ‎1‎ 侧视图 正视图 俯视图 ‎1‎ ‎3‎ ‎2‎ 侧视图 正视图 俯视图 ‎2‎ ‎3‎ ‎1‎ ‎ A. 9 B. 3 C. 20 D. 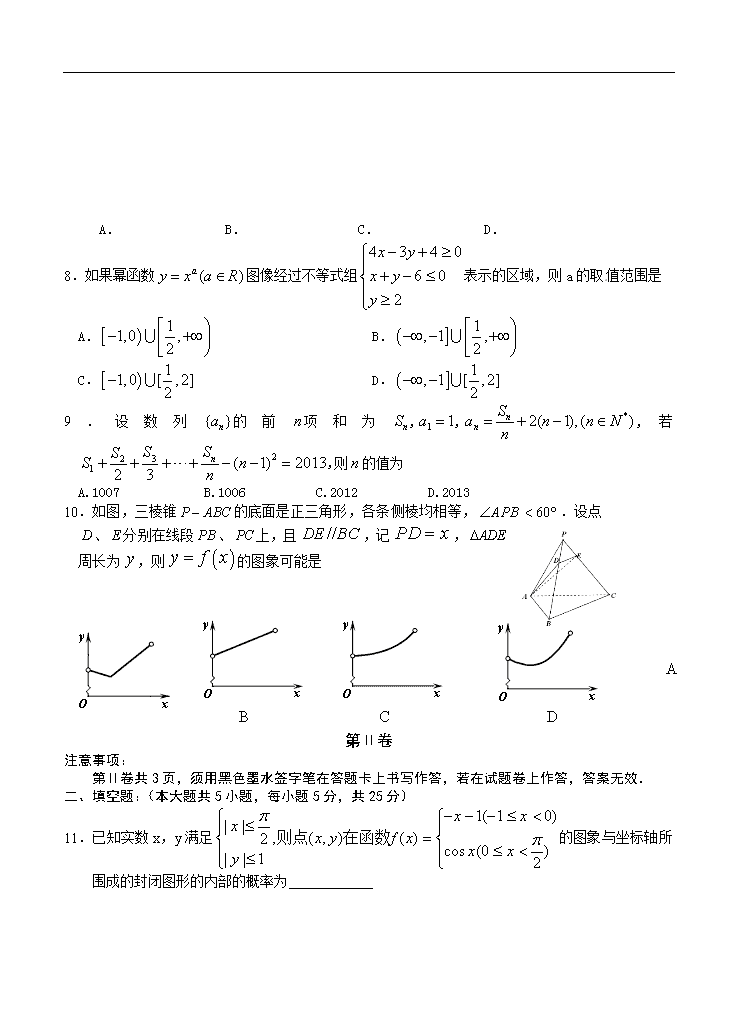-11‎ ‎7．已知以下三视图中有三个同时表示某一个三棱锥，则不是该三棱锥的三视图是 A． B． C． D．‎ ‎8．如果幂函数图像经过不等式组表示的区域，则a的取值范围是 A． B．‎ C． D．‎ ‎9．设数列的前项和为,,,若 ,则的值为 A.1007 B.1006 C.2012 D.2013‎ ‎10．如图，三棱锥的底面是正三角形，各条侧棱均相等，．设点 ‎、分别在线段、上，且，记，‎ 周长为，则的图象可能是 ‎ ‎ ‎ ‎ A B C D 第Ⅱ卷 注意事项：‎ ‎ 第Ⅱ卷共3页，须用黑色墨水签字笔在答题卡上书写作答，若在试题卷上作答，答案无效．‎ 二、填空题：（本大题共5小题，每小题5分，共25分）‎ ‎11．已知实数x，y满足的图象与坐标轴所围成的封闭图形的内部的概率为 ‎ ‎(第13题)‎ O A B C ‎12．已知以为周期的函数，其中。若方程 恰有5个实数解，则的取值范围为 ‎ ‎13．如图,在扇形中,,为弧上的一个动点.若 ‎，则的取值范围是 ．‎ ‎14．若函数在给定区间M上存在正数t，使得对于任意，有，且，则称为M上的t级类增函数。给出4个命题 ‎①函数上的3级类增函数 ‎②函数上的1级类增函数 ‎③若函数上的级类增函数，则实数a的最小值为2‎ ‎④设是定义在上的函数，且满足：1.对任意，恒有；2.对任意，恒有；3. 对任意，，若函数是上的t级类增函数，则实数t的取值范围为。‎ 以上命题中为真命题的是 ‎ 三、选做题：请考生在下列两题中选一题，则按所做的一题评分。本题共5分 ‎15．（考生注意：请在下列两题中任选一题作答，如果多做则按所做的第一题评分）‎ ‎ A．（不等式选讲）已知函数．若关于x的不等式的解集是，则的取值范围是 ‎ ‎ B．（坐标系与参数方程选做题）在极坐标系中，已知曲线与直线相切，则实数的值为_______‎ 四、解答题：（本大题共6小题，共75分，其中第16—19小题每题12分，第20题13分，第21题14分）‎ ‎16．（本小题满分12分）‎ 已知函数 在区间上单调递增,在区间上单调递减;如图,四边形中,,,为的内角的对边，‎ 且满足.‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）若，设，,‎ ‎，求四边形面积的最大值.‎ 17． ‎(本小题满分12分)‎ 某商场共五层，从五层下到四层有3个出口，从三层下到二层有4个出口，从二层下到一层有4个出口，从一层走出商场有6个出口。安全部门在每层安排了一名警员值班，负责该层的安保工作。假设每名警员到该层各出口处的时间相等，某罪犯在五楼犯案后，欲逃出商场，各警员同时接到指令，选择一个出口进行围堵。逃犯在每层选择出口是等可能的。已知他被三楼警员抓获的概率为。‎ ‎（Ⅰ）问四层下到三层有几个出口？‎ ‎（Ⅱ）天网恢恢，疏而不漏，犯罪嫌疑人最终落入法网。设抓到逃犯时，他已下了层楼，写出的分布列，并求。‎ ‎18．（本小题满分12分）‎ 如图，直角梯形与等腰直角三角形所在的平面互相垂直．∥，，，．‎ ‎（Ⅰ）求直线与平面所成角的正弦值； ‎ ‎（Ⅱ）线段上是否存在点，使// 平面？若存在，求出；若不存在，说明理由．‎ ‎19．（本小题满分12分）‎ 已知,数列满足,数列满足；又知数列中，，且对任意正整数，.‎ ‎（Ⅰ）求数列和数列的通项公式；‎ ‎（Ⅱ）将数列中的第项，第项，第项，……，第项，……删去后，剩余的项按从小到大的顺序排成新数列，求数列的前项和.‎ ‎20．(本题满分13分) ‎ ‎ 如图，F1，F2是离心率为的椭圆 C：(a＞b＞0)的左、右焦点，直线：x＝－将线段F1F2分成两段，其长度之比为1 : 3．设A，B是C上的两个动点，线段AB的中点M在直线l上，线段AB的中垂线与C交于P，Q两点．‎ ‎(Ⅰ) 求椭圆C的方程；‎ 第20题图 O B A x y x＝－‎ ‎2‎ ‎1‎ M F1‎ F2‎ P Q ‎(Ⅱ) 是否存在点M，使以PQ为直径的圆经过点F2，若存在，求出M点坐标，若不存在，请说明理由．‎ ‎21．（本小题满分14分） ‎ ‎ 已知函数，（其中，），且函数的图象在 点处的切线与函数的图象在点处的切线重合．‎ ‎（Ⅰ）求实数a，b的值；‎ ‎（Ⅱ）若，满足，求实数m的取值范围；‎ ‎2013届高三模拟试卷 数学（理）试卷参考答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C D C ‎ B C C D B A C 二、填空题 ‎11、 12、 13、 ‎ ‎14、①④ 15、A： ；B：或 三、解答题 ‎ 16．解：（Ⅰ）由题意知：，解得：， ………………………2分 ‎ ‎ ‎ ‎ ‎………………………………………4分 ‎……………………………………6分 ‎（Ⅱ）因为，所以，所以为等边三角形 ‎ …………8分 ‎，……………10分 ‎,， ‎ 当且仅当即时取最大值,的最大值为………12分 ‎17．解：（1）设四层下到三层有个出口，恰好被三楼的警员抓获，说明五层及四层的警员均没有与他相遇。‎ ‎ ，解得………………………3分 ‎ （2）可能取值为0,1,2,3,4,5‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ………………………8分 所以，分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ p ‎………………………………………………………………………………10分 ‎………………………12分 ‎18．解：（1）解法1：因为平面平面，且 所以BC⊥平面，则即为直线与平面所成的角………2分 设BC=a，则AB=2a，，所以 则直角三角形CBE中，‎ 即直线与平面所成角的正弦值为． ………………………6分 ‎ 解法2：因为平面平面，且 ，‎ 所以平面，所以． ‎ 由两两垂直，建立如图所示的空间直角坐标系． ‎ 因为三角形为等腰直角三角形，所以，设，‎ 则．‎ 所以 ，平面的一个法向量为．…………3分 设直线与平面所成的角为，‎ 所以 ， ‎ 即直线与平面所成角的正弦值为． …………………………6分 ‎ ‎（2）存在点，且时，有// 平面． ‎ 证明如下：由 ，，所以．‎ 设平面的法向量为，则有 所以 取，得．………………………………9分 ‎ 因为 ，且平面，所以 // 平面． ‎ 即点满足时，有// 平面．……………………………………12分 ‎ ‎19．解： , …………………3分 又由题知：令 ，则, ……………5分 若，则，，所以恒成立 若,当,不成立,所以 …………………………………6分 ‎（Ⅱ）由题知将数列中的第3项、第6项、第9项……删去后构成的新数列中的奇数列与偶数列仍成等比数列，首项分别是，公比均是 …………9分 ‎ ‎ ‎………………………………………12分 ‎20．解：(Ⅰ) 设F2(c，0)，则＝，所以c＝1．因为离心率e＝，所以a＝．‎ 所以椭圆C的方程为． …………………………………………4分 ‎ ‎(Ⅱ) 当直线AB垂直于x轴时，直线AB方程为x＝－，……………………6分 ‎ 此时P(，0)、Q(,0) ，．不合；‎ 当直线AB不垂直于x轴时，设存在点M(－，m) (m≠0)，直线AB的斜率为k， ，‎ ‎．由 得，则 －1＋4mk＝0，‎ 故k＝．此时，直线PQ斜率为，PQ的直线方程为．‎ 即 ．‎ 联立 消去y，整理得 ．‎ 所以，．………………………………8分 ‎ 由题意0，于是 ‎(x1－1)(x2－1)＋y1y2‎ ‎ ‎ ‎=0．‎ 因为M在椭圆内，符合条件；……………………12分 ‎ 综上，存在两点M符合条件，坐标为．……………………13分 ‎ 21． 解：（Ⅰ）∵，∴，‎ 则在点处切线的斜率，切点，‎ 则在点处切线方程为，……………………2分 ‎ 又，∴，‎ 则在点处切线的斜率，切点，‎ 则在点处切线方程为，…………………………4分 ‎ ‎ 由解得，．…………………………………………6分 ‎ ‎（Ⅱ）由得，故在上有解，‎ ‎ 令，只需．……………………………………8分 ‎ ‎①当时，，所以；………………………………10分 ‎ ‎②当时，∵，‎ ‎∵，∴，，∴，‎ 故，即函数在区间上单调递减，‎ 所以，此时．…………………………………………13分 ‎ 综合①②得实数m的取值范围是．………………14分