【数学】2021届一轮复习北师大版（文）第九章　第5讲　第1课时　椭圆及其性质学案 15页

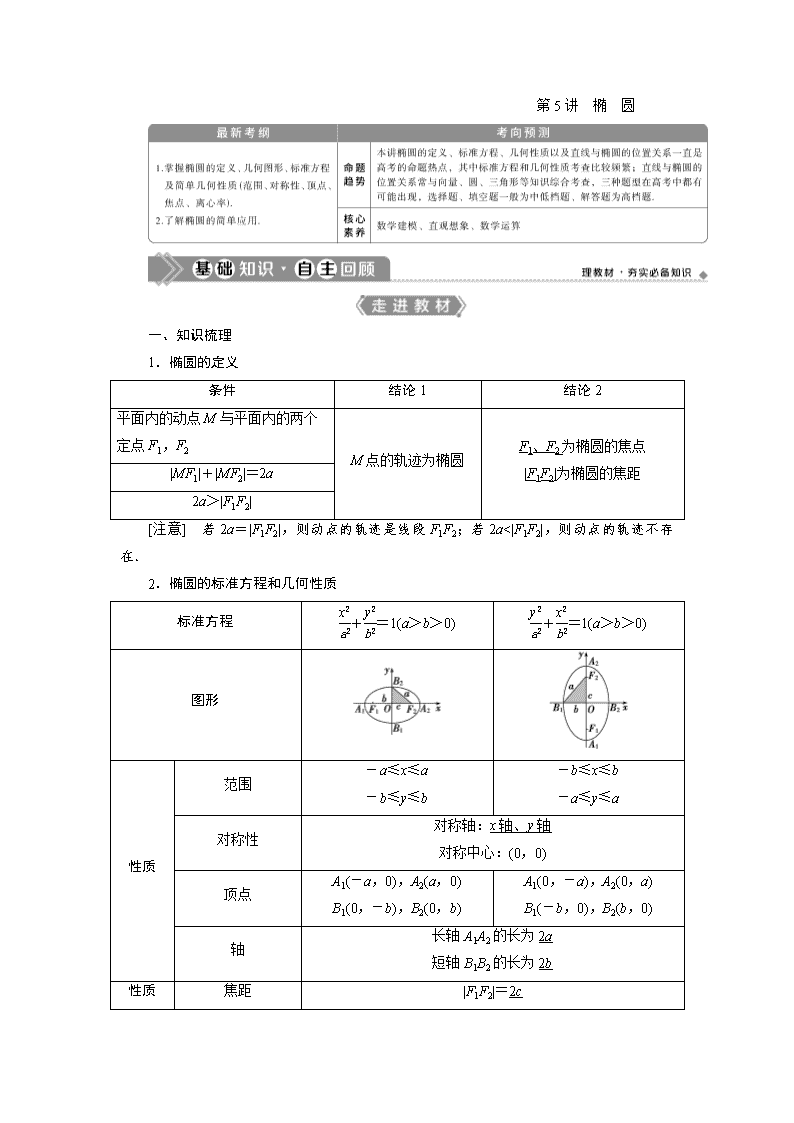
第5讲　椭　圆 一、知识梳理 ‎1．椭圆的定义 条件 结论1‎ 结论2‎ 平面内的动点M与平面内的两个定点F1，F2‎ M点的轨迹为椭圆 F1、F2为椭圆的焦点 ‎|F1F2|为椭圆的焦距 ‎|MF1|＋|MF2|＝2a ‎2a＞|F1F2|‎ ‎[注意]　若2a＝|F1F2|，则动点的轨迹是线段F1F2；若2a<|F1F2|，则动点的轨迹不存在．‎ ‎2．椭圆的标准方程和几何性质 标准方程 ＋＝1(a＞b＞0)‎ ＋＝1(a＞b＞0)‎ 图形 性质 范围 ‎－a≤x≤a ‎－b≤y≤b ‎－b≤x≤b ‎－a≤y≤a 对称性 对称轴：x轴、y轴 对称中心：(0，0)‎ 顶点 A1(－a，0)，A2(a，0)‎ B1(0，－b)，B2(0，b)‎ A1(0，－a)，A2(0，a)‎ B1(－b，0)，B2(b，0)‎ 轴 长轴A1A2的长为2a 短轴B1B2的长为2b 性质 焦距 ‎|F1F2|＝2c 离心率 e＝，e∈(0，1)‎ a，b，c的关系 c2＝a2－b2‎ 常用结论 ‎1．点P(x0，y0)和椭圆的位置关系 ‎(1)点P(x0，y0)在椭圆内⇔＋<1.‎ ‎(2)点P(x0，y0)在椭圆上⇔＋＝1.‎ ‎(3)点P(x0，y0)在椭圆外⇔＋>1.‎ ‎2．椭圆的常用性质 ‎(1)椭圆上的点到焦点距离的最大值为a＋c，最小值为a－c.‎ ‎(2)过椭圆的焦点且垂直于长轴的弦长为.‎ ‎(3)已知过焦点F1的弦AB，则△ABF2的周长为4a.‎ ‎(4)设P，A，B是椭圆上不同的三点，其中A，B关于原点对称，直线PA，PB斜率存在且不为0，则直线PA与PB的斜率之积为定值－.‎ 二、教材衍化 ‎ ‎1．椭圆16x2＋25y2＝400的长轴的长 ，离心率 ．‎ 答案：10　 ‎2．已知中心在原点的椭圆C的右焦点为F(1，0)，离心率等于，则C的方程是 ．‎ 答案：＋＝1‎ ‎3．椭圆C：＋＝1的左、右焦点分别为F1，F2，过F2的直线交椭圆C于A、B两点，则△F1AB的周长为 ，△AF1F2的周长为 ．‎ 答案：20　16‎ 一、思考辨析 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)平面内与两个定点F1，F2的距离之和等于常数的点的轨迹是椭圆．(　　)‎ ‎(2)椭圆的离心率e越大，椭圆就越圆．(　　)‎ ‎(3)椭圆既是轴对称图形，又是中心对称图形．(　　)‎ ‎(4)＋＝1(a≠b)表示焦点在y轴上的椭圆．(　　)‎ ‎(5)＋＝1(a>b>0)与＋＝1(a>b>0)的焦距相同．(　　)‎ 答案：(1)×　(2)×　(3)√　(4)×　(5)√‎ 二、易错纠偏 (1)忽视椭圆定义中的限制条件；‎ ‎(2)忽视椭圆标准方程焦点位置的讨论．‎ ‎1．平面内一点M到两定点F1(0，－9)，F2(0，9)的距离之和等于18，则点M的轨迹是 ．‎ 解析：由题意知|MF1|＋|MF2|＝18，但|F1F2|＝18，即|MF1|＋|MF2|＝|F1F2|，所以点M的轨迹是一条线段．‎ 答案：线段F1F2‎ ‎2．已知椭圆的长轴长为10，其焦点到中心的距离为4，则这个椭圆的标准方程为 ．‎ 答案：＋＝1或＋＝1‎ 第1课时　椭圆及其性质 ‎　　　　　　椭圆的定义及应用(典例迁移)‎ ‎ (1)(2020·黑龙江哈尔滨六中二模)设椭圆C：＋y2＝1的左焦点为F，直线l：y＝kx(k≠0)与椭圆C交于A，B两点，则|AF|＋|BF|的值是(　　)‎ A．2 B．2 ‎ C．4 D．4 ‎(2)(2020·宿州模拟)已知F1、F2是椭圆C：＋＝1(a＞b＞0)的两个焦点，P为椭圆C上的一点，且PF1⊥PF2，若△PF1F2的面积为9，则b＝ ．‎ ‎【解析】　(1)设椭圆的右焦点为F1，连接AF1，BF1，‎ 因为OA＝OB，OF＝OF1，‎ 所以四边形AFBF1是平行四边形．‎ 所以|BF|＝|AF1|，‎ 所以|AF|＋|BF|＝|AF|＋|AF1|＝2a＝4，故选C.‎ ‎(2)设|PF1|＝r1，|PF2|＝r2，‎ 则 所以2r1r2＝(r1＋r2)2－(r＋r)＝4a2－4c2＝4b2，‎ 所以S△PF1F2＝r1r2＝b2＝9，所以b＝3.‎ ‎【答案】　(1)C　(2)3‎ ‎【迁移探究】　(变条件)本例(2)中增加条件“△PF1F2的周长为18”，其他条件不变，求该椭圆的方程．‎ 解：由原题得b2＝a2－c2＝9，又2a＋2c＝18，所以a－c＝1，解得a＝5，故椭圆的方程为＋＝1.‎ 椭圆定义的应用主要有两个方面： 一是确认平面内与两定点有关的轨迹是否为椭圆；二是当P在椭圆上时，与椭圆的两焦点F1，F2组成的三角形通常称为“焦点三角形”，利用定义可求其周长，利用定义和余弦定理可求|PF1|·|PF2|，通过整体代入可求其面积等．‎ ‎1．已知椭圆＋＝1上一点P到椭圆一个焦点F1的距离为3，则P到另一个焦点F2的距离为(　　)‎ A．2 B．3 ‎ C．5 D．7‎ 解析：选D.因为a2＝25，所以2a＝10，所以由定义知，|PF1|＋|PF2|＝10，所以|PF2|＝10－|PF1|＝7.‎ ‎2．(2020·安徽马鞍山模拟)已知点F1，F2分别为椭圆C：＋＝1的左、右焦点，若点P在椭圆C上，且∠F1PF2＝60°，则S△F1PF2＝ ．‎ 解析：由|PF1|＋|PF2|＝4，|PF1|2＋|PF2|2－2|PF1|·|PF2|·cos 60°＝|F1F2|2，得3|PF1|·|PF2|＝12，所以|PF1|·|PF2|＝4，则S△F1PF2＝|PF1|·|PF2|sin∠F1PF2＝×4sin 60°＝.‎ 答案： ‎　　　　　　椭圆的标准方程(师生共研)‎ ‎ (1)(一题多解)过点(，－)，且与椭圆＋＝1有相同焦点的椭圆的标准方程为(　　)‎ A.＋＝1 B.＋＝1‎ C.＋＝1 D．＋＝1‎ ‎(2)若直线x－2y＋2＝0经过椭圆的一个焦点和一个顶点，则该椭圆的标准方程为 ．‎ ‎【解析】　(1)法一(定义法)：椭圆＋＝1的焦点为(0，－4)，(0，4)，即c＝4.‎ 由椭圆的定义知，2a＝＋，解得a＝2.‎ 由c2＝a2－b2，可得b2＝4.‎ 所以所求椭圆的标准方程为＋＝1.‎ 法二(待定系数法)：设所求椭圆方程为＋＝1(k<9)，将点(，－)的坐标代入，可得＋＝1，解得k＝5或k＝21(舍去)，所以所求椭圆的标准方程为＋＝1.‎ 法三(待定系数法)：设所求椭圆方程为＋＝1(a>b>0)．由题意得，解得，‎ 所以所求椭圆的标准方程为＋＝1.‎ ‎(2)直线与坐标轴的交点为(0，1)，(－2，0)，由题意知当焦点在x轴上时，c＝2，b＝1，‎ 所以a2＝5，所求椭圆的标准方程为＋y2＝1.‎ 当焦点在y轴上时，b＝2，c＝1，‎ 所以a2＝5，所求椭圆的标准方程为＋＝1.‎ ‎【答案】　(1)C　(2)＋y2＝1或＋＝1‎ ‎(1)用定义法求椭圆的标准方程 先根据椭圆的定义确定a2，b2的值，再结合焦点位置求出椭圆的方程．其中常用的关系有：‎ ‎①b2＝a2－c2；‎ ‎②椭圆上任意一点到椭圆两焦点的距离之和等于2a；‎ ‎③椭圆上一短轴顶点到一焦点的距离等于长半轴长a.‎ ‎(2)用待定系数法求椭圆的标准方程的步骤 ‎[提醒]　当椭圆焦点位置不明确时，可设为＋＝1(m>0，n>0，m≠n)，也可设为Ax2＋By2＝1(A>0，B>0，且A≠B)．‎ ‎1．已知动点M到两个定点A(－2，0)，B(2，0)的距离之和为6，则动点M的轨迹方程为(　　)‎ A.＋y2＝1 B.＋＝1‎ C.＋x2＝1 D．＋＝1‎ 解析：选D.由题意有6>2＋2＝4，故点M的轨迹为焦点在x轴上的椭圆，则2a＝6，c＝2，故a2＝9，所以b2＝a2－c2＝5，故椭圆的方程为＋＝1.故选D.‎ ‎2．设椭圆＋＝1(m>0，n>0)的右焦点为(2，0)，离心率为，则此椭圆的方程为 ．‎ 解析：椭圆的右焦点为(2，0)，所以m2－n2＝4，e＝＝，所以m＝2，代入m2－n2＝4，得n2＝4，所以椭圆方程为＋＝1.‎ 答案：＋＝1‎ ‎3．已知椭圆C的中心在原点，一个焦点F(－2，0)，且长轴长与短轴长的比是2∶，则椭圆C的方程是 ．‎ 解析：设椭圆C的方程为＋＝1(a>b>0)．‎ 由题意知 解得a2＝16，b2＝12.‎ 所以椭圆C的方程为＋＝1.‎ 答案：＋＝1‎ ‎　　　　　　椭圆的几何性质(多维探究)‎ 角度一　椭圆的长轴、短轴、焦距 ‎ (2020·抚州质检)已知椭圆＋＝1的长轴在x轴上，焦距为4，则m等于(　　)‎ A．8 B．7 ‎ C．6 D．5‎ ‎【解析】　因为椭圆＋＝1的长轴在x轴上，‎ 所以解得6b>0)的下顶点，M，N在椭圆上，若四边形OPMN为平行四边形，α为直线ON的倾斜角，若α∈，则椭圆C的离心率的取值范围为(　　)‎ A. B. C. D． ‎【解析】　(1)由题设知∠F1PF2＝90°，∠PF2F1＝60°，|F1F2|＝2c，所以|PF2|＝c，|PF1|＝c.‎ 由椭圆的定义得|PF1|＋|PF2|＝2a，即c＋c＝2a，‎ 所以(＋1)c＝2a，‎ 故椭圆C的离心率e＝＝＝－1.故选D.‎ ‎(2)因为OPMN是平行四边形，‎ 所以MN∥OP且MN＝OP，‎ 故yN＝，代入椭圆方程可得xN＝，‎ 所以kON＝＝tan α.‎ 又α∈，所以<<1，‎ 所以ab>0)的一个焦点是圆x2＋y2－6x＋8＝0的圆心，且短轴长为8，则椭圆的左顶点为(　　)‎ A．(－3，0) B．(－4，0) ‎ C．(－10，0) D．(－5，0)‎ 解析：选D.因为圆的标准方程为(x－3)2＋y2＝1，‎ 所以圆心坐标为(3，0)，所以c＝3.又b＝4，‎ 所以a＝＝5.‎ 因为椭圆的焦点在x轴上，‎ 所以椭圆的左顶点为(－5，0)．‎ ‎2．若点O和点F分别为椭圆＋＝1的中心和左焦点，点P为椭圆上的任意一点，则·的最大值为(　　)‎ A．2 B．3 ‎ C．6 D．8‎ 解析：选C.由椭圆＋＝1可得F(－1，0)，点O(0，0)，设P(x，y)(－2≤x≤2)，‎ 则·＝x2＋x＋y2＝x2＋x＋3 ‎＝x2＋x＋3＝(x＋2)2＋2，－2≤x≤2，‎ 当且仅当x＝2时，·取得最大值6.‎ ‎3．已知椭圆＋＝1(a>b>0)，F是椭圆的右焦点，A为左顶点，点P在椭圆上，PF⊥x轴，若|PF|＝|AF|，则椭圆的离心率为 ．‎ 解析：因为点P在椭圆上，且PF⊥x轴，所以|PF|＝，‎ 又因为|AF|＝a＋c，|PF|＝|AF|，‎ 所以4(a2－c2)＝a(a＋c)，即4(a－c)＝a，则3a＝4c，‎ 即＝.‎ 答案： ‎[基础题组练]‎ ‎1．已知正数m是2和8的等比中项，则圆锥曲线x2＋＝1的焦点坐标为(　　)‎ A．(±，0) B．(0，±)‎ C．(±，0)或(±，0) D．(0，±)或(±，0)‎ 解析：选B.因为正数m是2和8的等比中项，所以m2＝16，即m＝4，所以椭圆x2＋＝1的焦点坐标为(0，±)，故选B.‎ ‎2．(2019·高考北京卷)已知椭圆＋＝1(a＞b＞0)的离心率为，则(　　)‎ A．a2＝2b2 B．3a2＝4b2 ‎ C．a＝2b D．3a＝4b 解析：选B.由题意得，＝，所以＝，又a2＝b2＋c2，所以＝，＝，所以4b2＝3a2.故选B.‎ ‎3．曲线＋＝1与曲线＋＝1(k<144)的(　　)‎ A．长轴长相等 B．短轴长相等 C．离心率相等 D．焦距相等 解析：选D.曲线＋＝1中c2＝169－k－(144－k)＝25，所以c＝5，所以两曲线的焦距相等．‎ ‎4．(2020·郑州模拟)已知椭圆C：＋＝1(a>b>0)的左、右焦点分别为F1，F2，离心率为，过F2的直线l交C于A，B两点，若△AF1B的周长为12，则C的方程为(　　)‎ A.＋y2＝1 B.＋＝1‎ C.＋＝1 D．＋＝1‎ 解析：选D.由椭圆的定义，知|AF1|＋|AF2|＝2a，|BF1|＋|BF2|＝2a，所以△AF1B 的周长为|AF1|＋|AF2|＋|BF1|＋|BF2|＝4a＝12，所以a＝3.因为椭圆的离心率e＝＝，所以c＝2，所以b2＝a2－c2＝5，所以椭圆C的方程为＋＝1，故选D.‎ ‎5．(2020·昆明市诊断测试)已知F1，F2为椭圆C：＋＝1(a>b>0)的左、右焦点，B为C的短轴的一个端点，直线BF1与C的另一个交点为A，若△BAF2为等腰三角形，则＝(　　)‎ A. B. ‎ C. D．3‎ 解析：选A.如图，不妨设点B在y轴的正半轴上，根据椭圆的定义，得|BF1|＋|BF2|＝2a，|AF1|＋|AF2|＝2a，由题意知|AB|＝|AF2|，所以|BF1|＝|BF2|＝a，|AF1|＝，|AF2|＝.所以＝.故选A.‎ ‎6．若椭圆C：＋＝1(a>b>0)的短轴长等于焦距，则椭圆的离心率为 ．‎ 解析：由题意可得b＝c，则b2＝a2－c2＝c2，a＝c，‎ 故椭圆的离心率e＝＝.‎ 答案： ‎7．(2020·江西南昌模拟)若椭圆＋＝1(a>b>0)的离心率为，短轴长为4，则椭圆的标准方程为 ．‎ 解析：由题意可知e＝＝，2b＝4，得b＝2，‎ 所以解得 所以椭圆的标准方程为＋＝1.‎ 答案：＋＝1‎ ‎8．(2019·高考全国卷Ⅲ)设F1，F2为椭圆C：＋＝1的两个焦点，M为C上一点且在第一象限．若△MF1F2为等腰三角形，则M的坐标为 ．‎ 解析：通解：由椭圆C：＋＝1，得c＝＝4，不妨设F1，F2分别为左、右焦点，则由题意知|MF1|＝|F1F2|＝2c＝8，于是由椭圆的定义得|MF1|＋|MF2|＝12，所以|MF2|＝12－|MF1|＝4，易知△MF1F2的底边MF2上的高h＝＝＝2，所以|MF2|·h＝|F1F2|·yM，即×4×2＝×8×yM，解得yM＝，代入椭圆方程得xM＝－3(舍去)或xM＝3，故点M的坐标为(3，)．‎ 优解：不妨设F1，F2分别为左、右焦点，则由题意，得|MF1|＝|F1F2|＝8，由椭圆的焦半径公式得|MF1|＝exM＋6＝xM＋6＝8，解得xM＝3，代入椭圆方程得yM＝，故点M的坐标为(3，)．‎ 答案：(3，)‎ ‎9．已知椭圆的长轴长为10，两焦点F1，F2的坐标分别为(3，0)和(－3，0)．‎ ‎(1)求椭圆的标准方程；‎ ‎(2)若P为短轴的一个端点，求△F1PF2的面积．‎ 解：(1)设椭圆的标准方程为＋＝1(a>b>0)，‎ 依题意得因此a＝5，b＝4，‎ 所以椭圆的标准方程为＋＝1.‎ ‎(2)易知|yP|＝4，又c＝3，‎ 所以S△F1PF2＝|yP|×2c＝×4×6＝12.‎ ‎10．分别求出满足下列条件的椭圆的标准方程．‎ ‎(1)与椭圆＋＝1有相同的离心率且经过点(2，－)；‎ ‎(2)已知点P在以坐标轴为对称轴的椭圆上，且P到两焦点的距离分别为5，3，过P且与长轴垂直的直线恰过椭圆的一个焦点．‎ 解：(1)由题意，设所求椭圆的方程为＋＝t1或＋＝t2(t1，t2＞0)，因为椭圆过点(2，－)，所以t1＝＋＝2，或t2＝＋＝.‎ 故所求椭圆的标准方程为＋＝1或＋＝1.‎ ‎(2)由于焦点的位置不确定，所以设所求的椭圆方程为＋＝1(a＞b＞0)或＋＝1(a＞b＞0)，‎ 由已知条件得 解得a＝4，c＝2，所以b2＝12.‎ 故椭圆的方程为＋＝1或＋＝1.‎ ‎[综合题组练]‎ ‎1．(2020·合肥市第二次质量检测)已知椭圆＋＝1(a>b>0)的左、右焦点分别为F1，F2，右顶点为A，上顶点为B，以线段F1A为直径的圆交线段F1B的延长线于点P，若F2B∥AP，则该椭圆的离心率是(　　)‎ A. B. ‎ C. D． 解析：选D.如图，由题意知，P为以F1A为直径的圆上一点，所以F1P⊥AP，结合F2B∥AP知F1P⊥F2B.又|F1B|＝|F2B|，所以△BF1F2为等腰直角三角形，所以|OB|＝|OF2|，即b＝c，所以a2＝b2＋c2＝2c2，即a＝c，所以椭圆的离心率e＝＝，故选D.‎ ‎2．(2019·高考全国卷Ⅰ)已知椭圆C的焦点为F1(－1，0)，F2(1，0)，过F2的直线与C交于A，B两点．若|AF2|＝2|F2B|，|AB|＝|BF1|，则C的方程为(　　)‎ A.＋y2＝1 B.＋＝1‎ C.＋＝1 D．＋＝1‎ 解析：选B.由题意设椭圆的方程为＋＝1(a>b>0)，连接F1A，令|F2B|＝m，则|AF2|＝2m，|BF1|＝3m.由椭圆的定义知，4m＝2a，得m＝，故|F2A|＝a＝|F1A|，则点A为椭圆C 的上顶点或下顶点．令∠OAF2＝θ(O为坐标原点)，则sin θ＝.在等腰三角形ABF1中，cos 2θ＝＝，所以＝1－2()2，得a2＝3.又c2＝1，所以b2＝a2－c2＝2，椭圆C的方程为＋＝1.故选B.‎ ‎3．已知椭圆C：x2＋2y2＝4.‎ ‎(1)求椭圆C的离心率；‎ ‎(2)设O为原点．若点A在直线y＝2上，点B在椭圆C上，且OA⊥OB，求线段AB长度的最小值．‎ 解：(1)由题意，椭圆C的标准方程为＋＝1.‎ 所以a2＝4，b2＝2，从而c2＝a2－b2＝2.‎ 因此a＝2，c＝.‎ 故椭圆C的离心率e＝＝.‎ ‎(2)设点A，B的坐标分别为(t，2)，(x0，y0)，其中x0≠0.‎ 因为OA⊥OB，所以·＝0，‎ 即tx0＋2y0＝0，‎ 解得t＝－.又x＋2y＝4，‎ 所以|AB|2＝(x0－t)2＋(y0－2)2＝＋(y0－2)2‎ ‎＝x＋y＋＋4＝x＋＋＋4＝＋＋4(0