2012福州1月份质检理数试卷 8页

福建省福州市2012届高三第一学期期末质量检查数学（理）试卷（word版）‎ 第1卷(选择题 共50分)‎ ‎ 一、选择题(本大题共lO小题，每小题5分，共50分．在每小题所给的四个答案中有且只有一个答案是正确的．把正确的选项涂在答题卡的相应位置上．)‎ ‎ 1．已知集合A=，B=，那么集合( A) n B等于 ‎ A． B． C． D．‎ ‎2．复数(i为虚数单位)等于 A． B． C． D．‎ ‎3．“cosα =”是“cosα2α= -”的 A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎4．执行如图所示的程序框图，若输入x=0.1，则输出m的值是 A．0 B．0.1 C．1 D．-1‎ ‎ 5．将函数f (x)=sin2 x (x∈R)的图象向右平移个单位，则所得到的图象对应的函数的一个单调递增区间是 A．(-，0) B．(0，) C．(，) D．(，π)‎ ‎6．已知=1，=2，与的夹角为120°，++=0，则与的夹角为 A．150° B．90° C．60° D．30°‎ ‎7．已知g(x)为三次函数 f (x)=x3 +ax2+cx的导函数，则它们的图象可能是 ‎ 8．在三次独立重复试验中，事件A在每次试验中发生的概率相同，若事件A至少发生一 次的概率为，则事件A恰好发生一次的概率为 A． B． C． D．‎ ‎ 9．直线y=一x与椭圆C： =1(a>b>0)交于A、B两点，以线段AB为直径的圆恰好经过椭圆的右焦点，则椭圆C的离心率为A．B．C．D．‎ A． B． C． D．4-2‎ ‎10．设Q为有理数集，函数f (x) = g(x)=，则函数h(x)= f (x)·g(x)‎ A．是奇函数但不是偶函数 B．是偶函数但不是奇函数 C．既是奇函数也是偶函数 D．既不是偶函数也不是奇函数 ‎ ‎ 第Ⅱ卷(非选择题共1 00分)‎ 二、填空题(本大题共5小题。每小题4分。共20分，将答案填在答题卡的相应位置上．)‎ ‎11．计算的值等于 ．‎ ‎12．在(1+)2一(1+)4的展开式中，x的系数等于 ．(用数字作答)‎ ‎13．在圆x2+y2=4所围成的区域内随机取一个点P(x，y)，则| x |+| y | ≤ 2的概率为 ．‎ ‎14．“无字证明”(proofs without words)，就是将数学命题用简单、有创意而且易于理解的几何图形来呈现．请利用图甲、图乙中阴影部分的面积关系，写出该图所验证的一个三角恒等变换公式： ．‎ ‎15．如图的倒三角形数阵满足：(1)第1行的，n个数，分别是1，3，5，…， 2n-1；(2)从第二行起，各行中的每一个数都等于它肩上的两数之和；(3)数阵共有n行．问：当n=2012时，第32行的第17个数是 ．‎ 三．、解答题(本大题共6小题，共80分，解答应写出文字说明、证明过程或演算过程)‎ ‎16．(本小题满分l 3分)‎ 在数列{an}中，a1=2，an+l=an+cn (n∈N*，常数c≠0)，且a1，a2，a3成等比数列．‎ ‎(I)求c的值；‎ ‎(Ⅱ)求数列{an}的通项公式．‎ ‎17．(本小题满分13分)‎ 某学院为了调查本校学生201 1年9月“健康上网”‎ ‎(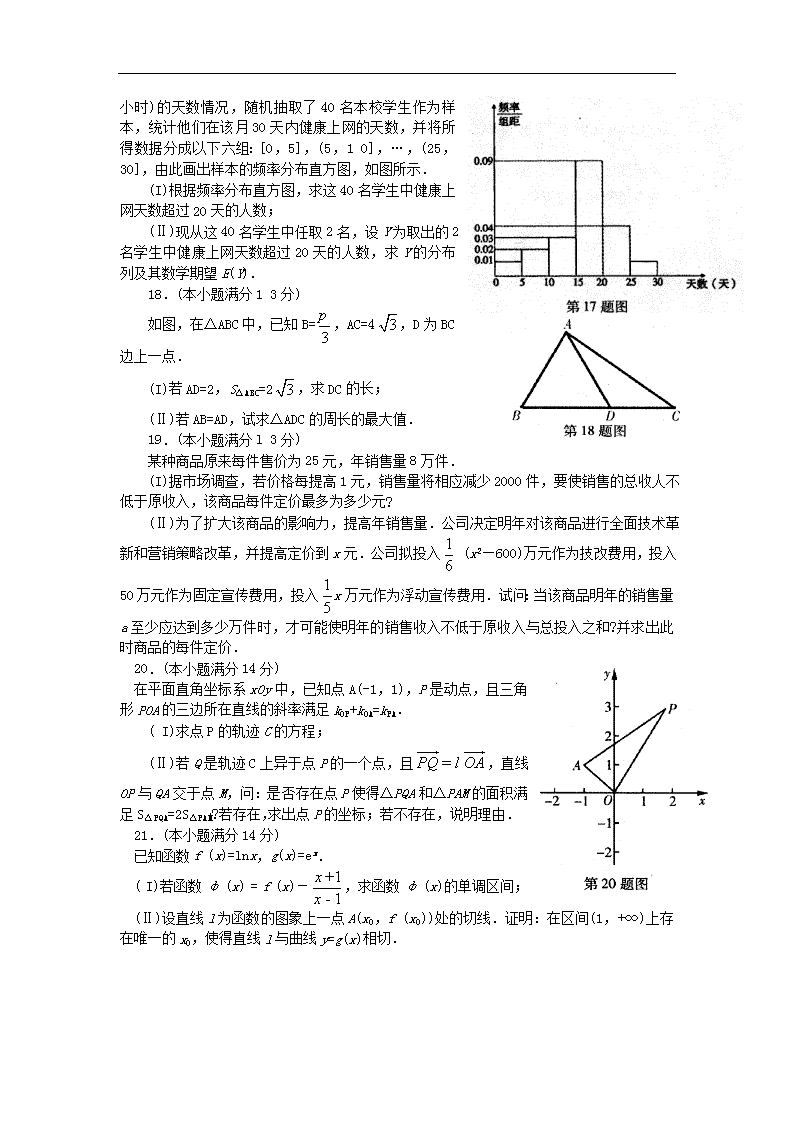健康上网是指每天上网不超过两小时)的天数情况，随机抽取了40名本校学生作为样本，统计他们在该月30天内健康上网的天数，并将所得数据分成以下六组：[O，5]，(5，1 O]，…，(25，30]，由此画出样本的频率分布直方图，如图所示．‎ ‎ (I)根据频率分布直方图，求这40名学生中健康上网天数超过20天的人数；‎ ‎ (Ⅱ)现从这40名学生中任取2名，设Y为取出的2名学生中健康上网天数超过20天的人数，求Y的分布列及其数学期望E(Y)．‎ ‎18．(本小题满分1 3分)‎ 如图，在△ABC中，已知B=，AC=4，D为BC边上一点．‎ ‎(I)若AD=2，S△ABC=2，求DC的长；‎ ‎(Ⅱ)若AB=AD，试求△ADC的周长的最大值．‎ ‎ 19．(本小题满分l 3分)‎ ‎ 某种商品原来每件售价为25元，年销售量8万件．‎ ‎ (I)据市场调查，若价格每提高1元，销售量将相应减少2000件，要使销售的总收人不低于原收入，该商品每件定价最多为多少元?‎ ‎ (Ⅱ)为了扩大该商品的影响力，提高年销售量．公司决定明年对该商品进行全面技术革新和营销策略改革，并提高定价到x元．公司拟投入 (x2—600)万元作为技改费用，投入50万元作为固定宣传费用，投入x万元作为浮动宣传费用．试问：当该商品明年的销售量a至少应达到多少万件时，才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价．‎ ‎ 20．(本小题满分14分)‎ ‎ 在平面直角坐标系xOy中，已知点A(-1，1)，P是动点，且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA．‎ ‎ ( I)求点P的轨迹C的方程；‎ ‎ (Ⅱ)若Q是轨迹C上异于点P的一个点，且，直线OP与QA交于点M，问：是否存在点P使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在，求出点P的坐标；若不存在，说明理由．‎ ‎ 21．(本小题满分14分)‎ ‎ 已知函数f (x)=lnx，g(x)=ex．‎ ‎ ( I)若函数φ (x) = f (x)－，求函数φ (x)的单调区间；‎ ‎ (Ⅱ)设直线l为函数的图象上一点A(x0，f (x0))处的切线．证明：在区间(1，+∞)上存在唯一的x0，使得直线l与曲线y=g(x)相切．‎ 福州市2011—2012学年第一学期期末高三质量检查 数学（理科）试卷参考答案及评分标准 一、选择题（本大题共10小题，每小题5分，共50分. 在每小题所给的四个答案中有且只有一个答案是正确的）‎ ‎1．B 2．D 3．A 4．A 5．B 6．B 7．D 8．C 9．C 10．A 二、填空题（本大题共5小题，每小题4分，共20分，将答案填在题后的横线上．）‎ ‎11．2 12． 13． 14． 15．‎ 三、解答题（本大题共6小题，共80分，解答应写出文字说明、证明过程或演算过程）‎ ‎16． （本小题满分13分）‎ 解：（Ⅰ）由题知，，，， 2分 因为，，成等比数列，所以， 4分 解得或，又，故． 6分 ‎（Ⅱ）当时，由得 ‎，‎ ‎，‎ ‎…‎ ‎，‎ 以上各式相加，得， 9分 又，，故， 11分 当时上式也成立， 12分 所以数列的通项公式为．（）． 13分 ‎17．（本小题满分13分）‎ 解：（Ⅰ）由图可知，健康上网天数未超过20天的频率为 ‎， 2分 ‎∴ 健康上网天数超过20天的学生人数是 ‎ ． 4分 ‎（Ⅱ）随机变量Y的所有可能取值为0,1,2． 5分 P(Y=0)=, 6分 ‎ P(Y=1)= , 7分 ‎ P(Y=2)= ． 8分 ‎ 所以Y的分布列为 Y ‎0‎ ‎1‎ ‎2‎ P ‎ 11分 ‎∴ E（Y）=0×+1×+2×= ． 13分 ‎18．（本小题满分13分）‎ 解：(Ⅰ) ，‎ ‎ ， ‎ ‎∴． 2分 ‎∵,‎ ‎∴． 3分 在△ADC中，由余弦定理，得 ‎ ‎, 4分 ‎, ‎ ‎． 6分 ‎（Ⅱ）∵，，‎ ‎∴ 为正三角形，‎ 在中，根据正弦定理，可得 ‎ , 7分 ‎，, 8分 ‎∴的周长为 ‎ 9分 ‎, 10分 ‎， 11分 ‎ 的周长最大值为． 13分 ‎19．（本小题满分13分）‎ 解：（Ⅰ）设每件定价为元，‎ 依题意，有， 3分 整理得，‎ 解得． 5分 ‎∴要使销售的总收入不低于原收入，每件定价最多为40元． 6分 ‎（Ⅱ）依题意，时，‎ 不等式有解, 8分 等价于时，有解, 9分 ‎ , 11分 ‎. 12分 ‎． ∴当该商品明年的销售量至少应达到10.2万件时，才可能使明年的销售收入不低于原收入与总投入之和，此时该商品的每件定价为30元． 13分 ‎20．（本小题满分14分）‎ 解：（Ⅰ）设点为所求轨迹上的任意一点，则由得，‎ ‎，‎ 整理得轨迹的方程为（且）. 4分 ‎（Ⅱ）方法一、‎ 设，‎ 由可知直线，则，‎ 故，即， 6分 由三点共线可知，‎ 与共线，‎ ‎∴ ， ‎ 由（Ⅰ）知，故， 8分 同理，由与共线，‎ ‎∴ ，‎ 即， ‎ 由（Ⅰ）知，故， 10分 将，代入上式得，‎ 整理得，‎ 由得， 12分 由，得到，因为，所以，‎ 由，得，∴的坐标为． 14分 方法二、设 由可知直线，则，‎ 故，即， 6分 ‎∴直线OP方程为： ①； 8分 直线QA的斜率为：， ‎ ‎∴直线QA方程为：，即 ②； 10分 联立①②，得，∴点M的横坐标为定值． 12分 由，得到，因为，所以，‎ 由，得，∴的坐标为． 14分 ‎21．（本小题满分14分）‎ 解：（Ⅰ） ，‎ ‎． 2分 ‎∵且，‎ ‎∴‎ ‎∴函数的单调递增区间为． 4分 ‎ （Ⅱ）∵ ，∴，‎ ‎∴ 切线的方程为,‎ ‎ 即, ① 6分 设直线与曲线相切于点，‎ ‎∵，∴，∴． 8分 ‎ ∴直线也为， ‎ 即， ② 9分 ‎ 由①②得 ，‎ ‎∴． 11分 ‎ 下证：在区间（1，+）上存在且唯一.‎ 由（Ⅰ）可知，在区间上递增．‎ 又，， 13分 ‎ 结合零点存在性定理，说明方程必在区间上有唯一的根，这个根就是所求的唯一． ‎ 故结论成立． ‎