【数学】2019届一轮复习北师大版　集合的概念与运算学案 12页

第一章　集合与常用逻辑用语 第1讲　集合的概念与运算 考纲要求 考情分析 命题趋势 ‎1.了解集合的含义、元素与集合的属于关系．‎ ‎2．能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题．‎ ‎3．理解集合之间包含与相等的含义，能识别给定集合的子集．‎ ‎4．在具体情境中了解全集与空集的含义．‎ ‎5．理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集．‎ ‎6．理解在给定集合中一个子集的补集的含义，会求给定子集的补集．‎ ‎7．能使用韦恩(Venn)图表达集合的关系及运算.‎ ‎2017·全国卷Ⅰ，1‎ ‎2017·全国卷Ⅱ，1‎ ‎2017·全国卷Ⅲ，1‎ ‎2017·天津卷，1‎ ‎2017·山东卷，1‎ ‎2017·浙江卷，1‎ ‎1.求集合的元素或元素的个数．‎ ‎2．根据集合间的关系求集合子集的个数、参数的取值或范围，判断集合的关系．‎ ‎3．集合间的运算：交集、并集、补集等．‎ ‎4．常以一些特殊符号⊕，⊗，*等来连接两个集合，赋予集合一种新运算，或者给集合一种新背景．‎ ‎5．常运用数轴或韦恩图及数形结合思想来求解含未知参数的集合间的关系、运算，常用分类讨论求解.‎ 分值：5分 ‎1．元素与集合 ‎(1)集合元素的特性：__确定性__、__互异性__、无序性．‎ ‎(2)集合与元素的关系：若a属于集合A，记作__a∈A__；若b不属于集合A，记作__b∉A__.‎ ‎(3)集合的表示方法：__列举法__、__描述法__、图示法．‎ ‎(4)常见数集及其符号表示 数集 自然数集 正整数集 整数集 有理数集 实数集 符号 N N*或N＋‎ Z Q R ‎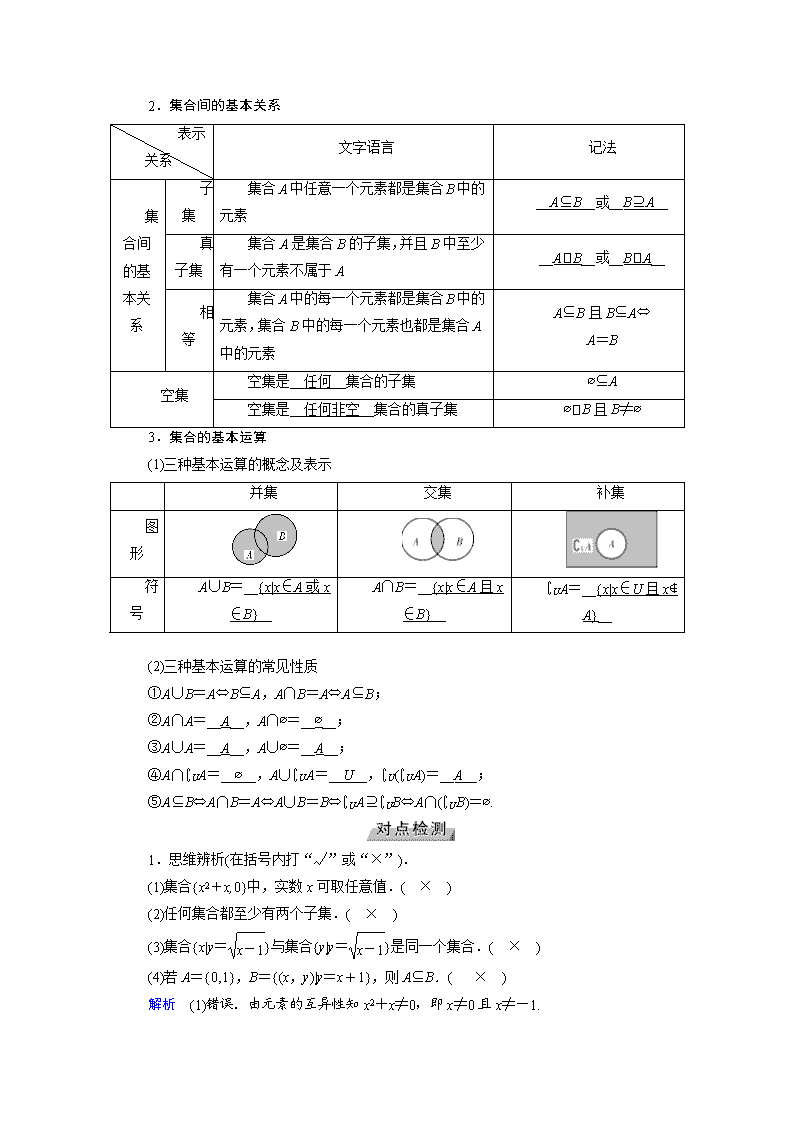2．集合间的基本关系 表示 关系　‎ 文字语言 记法 集合间的基本关系 子集 集合A中任意一个元素都是集合B中的元素 ‎__A⊆B__或__B⊇A__‎ 真子集 集合A是集合B的子集，并且B中至少有一个元素不属于A ‎__AB__或__BA__‎ 相等 集合A中的每一个元素都是集合B中的元素，集合B中的每一个元素也都是集合A中的元素 A⊆B且B⊆A⇔‎ A＝B 空集 空集是__任何__集合的子集 ‎∅⊆A 空集是__任何非空__集合的真子集 ‎∅B且B≠∅‎ ‎3．集合的基本运算 ‎(1)三种基本运算的概念及表示 并集 交集 补集 图形 符号 A∪B＝__{x|x∈A或x∈B}__‎ A∩B＝__{x|x∈A且x∈B}__‎ ‎∁UA＝__{x|x∈U且x∉A}__‎ ‎(2)三种基本运算的常见性质 ‎①A∪B＝A⇔B⊆A，A∩B＝A⇔A⊆B；‎ ‎②A∩A＝__A__，A∩∅＝__∅__；‎ ‎③A∪A＝__A__，A∪∅＝__A__；‎ ‎④A∩∁UA＝__∅__，A∪∁UA＝__U__，∁U(∁UA)＝__A__；‎ ‎⑤A⊆B⇔A∩B＝A⇔A∪B＝B⇔∁UA⊇∁UB⇔A∩(∁UB)＝∅.‎ ‎1．思维辨析(在括号内打“√”或“×”)．‎ ‎(1)集合{x2＋x,0}中，实数x可取任意值．(　×　)‎ ‎(2)任何集合都至少有两个子集．(　×　)‎ ‎(3)集合{x|y＝}与集合{y|y＝}是同一个集合．(　×　)‎ ‎(4)若A＝{0,1}，B＝{(x，y)|y＝x＋1}，则A⊆B．(　 ×　)‎ 解析　(1)错误．由元素的互异性知x2＋x≠0，即x≠0且x≠－1.‎ ‎(2)错误．∅只有一个子集．‎ ‎(3)错误．{x|y＝}＝{x|x≥1}，{y|y＝}＝{y|y≥0}．‎ ‎(4)错误．集合A是数集，集合B是点集．‎ ‎2．已知全集U＝R，那么正确表示集合M＝{－1,0,1}和N＝{x|x2＋x＝0}关系的韦恩(Venn)图是(　B　)‎ 解析　∵M＝{－1,0,1}，N＝{0，－1}，∴NM.故选B．‎ ‎3．(2017·全国卷Ⅲ)已知集合A＝{1,2,3,4}，B＝{2,4,6,8}，则A∩B中元素的个数为(　B　)‎ A．1　　　 B．‎2　‎　　‎ C．3　　　 D．4‎ 解析　A，B两集合中有两个公共元素2,4.故选B．‎ ‎4．(2017·北京卷)已知全集U＝R，集合A＝{x|x<－2或x>2}，则∁UA＝(　C　)‎ A．(－2,2)　　　 B．(－∞，－2)∪(2，＋∞)‎ C．[－2,2]　　　 D．(－∞，－2]∪[2，＋∞)‎ 解析　由已知可得集合A的补集∁UA＝[－2,2]．‎ ‎5．(2017·浙江卷)已知集合P＝{x|－10}，∴∁RP＝{y|y>1}，∴∁RP⊆Q.故选C．‎ ‎(2)∵B⊆A，∴①若B＝∅，则‎2m－10}，‎ ‎∴A∩B＝(0,1)．故选B．‎ ‎(2)∵2x(x－2)<1，∴x(x－2)<0，∴00，∴x<1，即B＝{x|x<1}，‎ ‎∴A∩B＝{x|00时，A＝.‎ ‎∵A⊆B，∴解得a≥2.‎ ‎②当a<0时，A＝.‎ ‎∵A⊆B，∴解得a≤－2.‎ ‎③当a＝0时，A＝∅⊆B，‎ 综上所述，a的取值范围是{a|a≥2或a≤－2或a＝0}．‎ ‎【跟踪训练2】 已知集合A＝{x∈R|x2＋x－6＝0}，B＝{x∈R|ax－1＝0}，若B⊆A，则实数a的值为(　D　)‎ A．或－ B．－或 C．或－或0 D．－或或0‎ 解析　由题意知集合A＝{2，－3}．‎ 当a＝0时，B＝∅，满足B⊆A；‎ 当a≠0时，ax－1＝0的解为x＝，‎ 由B⊆A可得＝－3或＝2，得a＝－或a＝.‎ 综上，a的值为－或或0.‎ 课时达标　第1讲 ‎[解密考纲]本考点考查集合中元素的性质、集合之间的关系、集合的运算(一般以不等式、函数、方程为载体)，一般以选择题、填空题的形式呈现，排在靠前的位置，题目难度不大．‎ 一、选择题 ‎1．已知全集U＝{1,2,3,4,5,6,7}，集合A＝{1,3,5,6}，则∁UA＝(　C　)‎ A．{1,3,5,6}　　　 B．{2,3,7}‎ C．{2,4,7}　　　 D．{2,5,7}‎ 解析　由补集的定义，得∁UA＝{2,4,7}．故选C．‎ ‎2．设集合A＝{1,2,3}，B＝{2,3,4}，则A∪B＝(　A　)‎ A．{1,2,3,4}　　　 B．{1,2,3}‎ C．{2,3,4}　　　 D．{1,3,4}‎ 解析　依题意得A∪B＝{1,2,3,4}．故选A．‎ ‎3．(2017·全国卷Ⅰ)已知集合A＝{x|x＜2}，B＝{x|3－2x＞0}，则(　A　)‎ A．A∩B＝　　　 B．A∩B＝∅‎ C．A∪B＝　　　 D．A∪B＝R 解析　因为A＝{x|x<2}，B＝{x|3－2x>0}＝x，所以A∩B＝x，A∪B＝{x|x<2}．故选A．‎ ‎4．已知集合A＝{y|y＝|x|－1，x∈R}，B＝{x|x≥2}，则下列结论正确的是(　C　)‎ A．－3∈A　　　 B．3∉B C．A∩B＝B　　　 D．A∪B＝B 解析　由题知A＝{y|y≥－1}，因此A∩B＝{x|x≥2}＝B．故选C．‎ ‎5．若集合A＝{－1,1}，B＝{0,2}，则集合{z|z＝x＋y，x∈A，y∈B}中的元素的个数为(　C　)‎ A．5　　　 B．4‎ C．3　　　 D．2‎ 解析　当x＝－1，y＝0时，z＝－1；当x＝－1，y＝2时，z＝1；当x＝1，y＝0时，z＝1；当x＝1，y＝2时，z＝3，故集合{z|z＝x＋y，x∈A，y∈B}中的元素的个数为3.故选C．‎ ‎6．满足M⊆{a1，a2，a3，a4}，且M∩{a1，a2，a3}＝{a1，a2}的集合M的个数是(　B　)‎ A．1　　　 B．2‎ C．3　　　 D．4‎ 解析　由题意可知a1，a2∈M且a3∉M，所以M＝{a1，a2}或M＝{a1，a2，a4}．故选B．‎ 二、填空题 ‎7．设集合M＝，N＝{x|x2≤x}，则M∩N＝____.‎ 解析　因为N＝[0,1]，所以M∩N＝.‎ ‎8．若{3,4，m2－‎3m－1}∩{‎2m，－3}＝{－3}，则m＝__1__.‎ 解析　由集合中元素的互异性，可得所以m＝1.‎ ‎9．已知集合A＝，B＝{x|x＋m2≥1}，若A⊆B，则实数m的取值范围是__∪__.‎ 解析　因为y＝2＋，x∈，所以y∈.又因为A⊆B，所以1－m2≤，解得m≥或m≤－.‎ 三、解答题 ‎10．(2018·黑龙江伊春二中期中)已知全集为R，集合A＝{x|x≥2或x＜0}，B＝{x|1＜x≤3}，求A∩B，A∪B，∁RA．‎ 解析　因为集合A＝{x|x≥2或x<0}，所以根据交集的定义可得A∩B＝{x|2≤x≤3}，根据并集的定义可求得A∪B＝{x<0或x>1}，因为全集为R，所以根据补集的定义可求得∁RA＝‎ ‎{x|0≤x<2}．‎ ‎11．(2018·黑龙江双鸭山第一中学期中)已知集合P＝{x|a＋1≤x≤‎2a＋1}，集合Q＝{x|－2≤x≤5}．‎ ‎(1)若a＝3，求集合(∁RP)∩Q；‎ ‎(2)若P⊆Q，求实数a的取值范围．‎ 解析　(1)当a＝3时，P＝{x|4≤x≤7}，‎ ‎∴∁RP＝{x|x<4或x>7}，‎ ‎∴(∁RP)∩Q＝{x|x<4或x>7}∩{x|－2≤x≤5}＝{x|－2≤x<4}．‎ ‎(2)①当P＝∅时，满足P⊆Q，有‎2a＋1