2020高考数学二轮复习练习：第二部分 54分专项练 54分专项练（三） 18、19、20、21含解析 6页

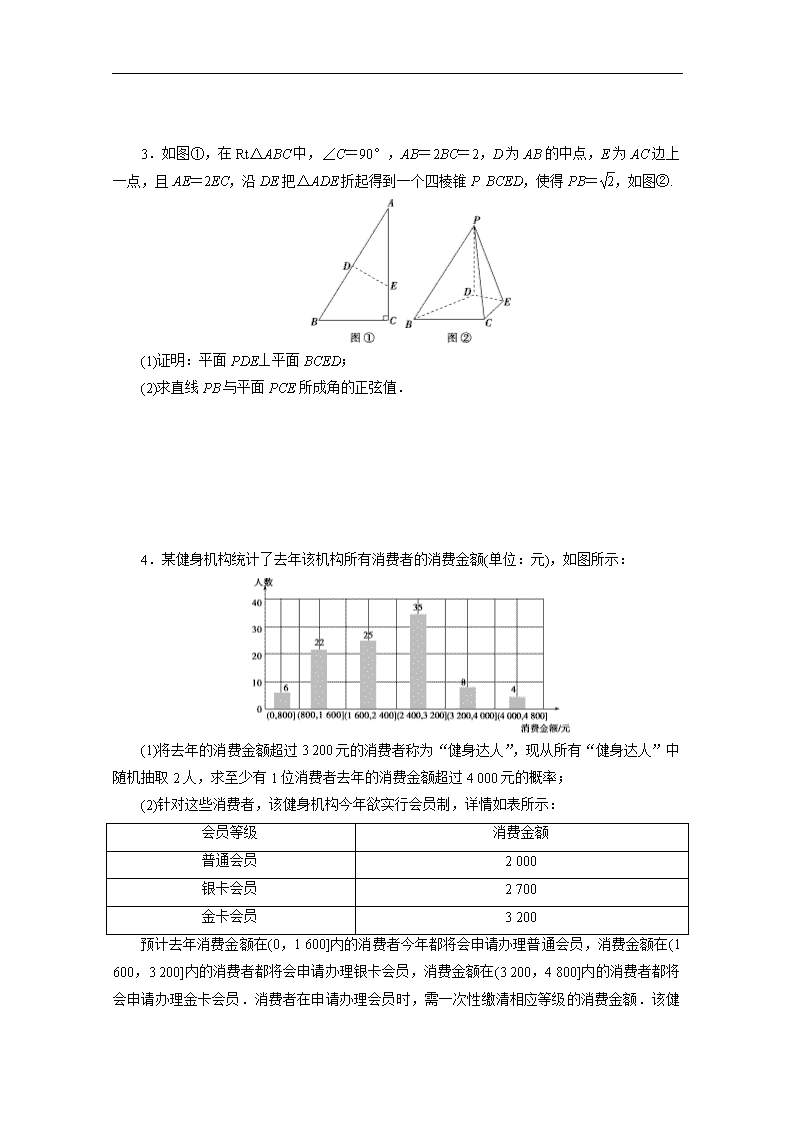
‎54分专项练(三)　18、19、20、21‎ ‎1．在△ABC中，内角A、B、C的对边分别为a、b、c，且acos B＋bsin A＝c.‎ ‎(1)求角A的大小；‎ ‎(2)若a＝，△ABC的面积为，求b＋c的值．‎ ‎2．已知数列{an}的前n项和为Sn，数列是首项为1，公差为2的等差数列．‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)设数列{bn}满足＋＋…＋＝5－(4n＋5)·，求数列{bn}的前n项和Tn.‎ ‎3．如图①，在Rt△ABC中，∠C＝90°，AB＝2BC＝2，D为AB的中点，E为AC边上一点，且AE＝2EC，沿DE把△ADE折起得到一个四棱锥PBCED，使得PB＝，如图②.‎ ‎(1)证明：平面PDE⊥平面BCED；‎ ‎(2)求直线PB与平面PCE所成角的正弦值．‎ ‎4．某健身机构统计了去年该机构所有消费者的消费金额(单位：元)，如图所示：‎ ‎(1)将去年的消费金额超过3 200元的消费者称为“健身达人”，现从所有“健身达人”中随机抽取2人，求至少有1位消费者去年的消费金额超过4 000元的概率；‎ ‎(2)针对这些消费者，该健身机构今年欲实行会员制，详情如表所示：‎ 会员等级 消费金额 普通会员 ‎2 000‎ 银卡会员 ‎2 700‎ 金卡会员 ‎3 200‎ 预计去年消费金额在(0，1 600]内的消费者今年都将会申请办理普通会员，消费金额在(1 600，3 200]内的消费者都将会申请办理银卡会员，消费金额在(3 200，4 800]内的消费者都将会申请办理金卡会员．消费者在申请办理会员时，需一次性缴清相应等级的消费金额．‎ 该健身机构在今年底将针对这些消费者举办消费返利活动，现有如下两种预设方案：‎ 方案1：按分层抽样从普通会员、银卡会员、金卡会员中总共抽取25位“幸运之星”给予奖励．普通会员中的“幸运之星”每人奖励500元，银卡会员中的“幸运之星”每人奖励600元，金卡会员中的“幸运之星”每人奖励800元．‎ 方案2：每位会员均可参加摸奖游戏，游戏规则如下：从一个装有3个白球、2个红球(球只有颜色不同)的箱子中，有放回地摸三次球，每次只能摸一个球．若摸到红球的总数为2，则可获得200元奖励金；若摸到红球的总数为3，则可获得300元奖励金；其他情况不给予奖励．规定每位普通会员均可参加1次摸奖游戏，每位银卡会员均可参加2次摸奖游戏，每位金卡会员均可参加3次摸奖游戏(每次摸奖的结果相互独立)．‎ 以奖励金的数学期望为依据，请你预测哪一种方案投资较少？并说明理由．‎ ‎ ‎ ‎54分专项练(三)　18、19、20、21‎ ‎1．解：(1)△ABC中，acos B＋bsin A＝c，‎ 由正弦定理得sin Acos B＋sin Bsin A＝sin C，‎ 又sin C＝sin(A＋B)＝sin Acos B＋cos Asin B，‎ 所以sin Bsin A＝cos Asin B，又sin B≠0，所以sin A＝cos A，‎ 又A∈(0，π)，所以tan A＝1，A＝.‎ ‎(2)由S△ABC＝bcsin A＝bc＝，‎ 解得bc＝2－；‎ 又a2＝b2＋c2－2bccos A，所以2＝b2＋c2－bc＝(b＋c)2－(2＋)bc，‎ 所以(b＋c)2＝2＋(2＋)bc＝2＋(2＋)(2－)＝4，所以b＋c＝2.‎ ‎2．解：(1)因为数列是首项为1，公差为2的等差数列，‎ 所以＝1＋2(n－1)＝2n－1，‎ 所以Sn＝2n2－n.‎ 当n＝1时，a1＝S1＝1；‎ 当n≥2时，an＝Sn－Sn－1＝(2n2－n)－[2(n－1)2－(n－1)]＝4n－3.‎ 当n＝1时，a1＝1也符合上式，‎ 所以数列{an}的通项公式为an＝4n－3.‎ ‎(2)当n＝1时，＝，所以b1＝2a1＝2.‎ 当n≥2时，由＋＋…＋＝5－(4n＋5)，①‎ 得＋＋…＋＝5－(4n＋1).②‎ ‎①－②，得＝(4n－3).‎ 因为an＝4n－3，所以bn＝＝2n(当n＝1时也符合)，‎ 所以＝＝2，所以数列{bn}是首项为2，公比为2的等比数列，所以Tn＝＝2n＋1－2.‎ ‎3．解：(1)证明：因为∠C＝90°，AB＝2BC＝2，所以AC＝，∠A＝30°.‎ 因为AE＝2EC，所以AE＝AC＝.‎ 在△ADE中，由余弦定理得DE2＝AD2＋AE2－2AD·AEcos A＝12＋－2×1××＝，所以DE＝，‎ 所以AD2＋DE2＝AE2，所以DE⊥AB，所以PD⊥DE.‎ 又因为PD＝BD＝1，PB＝，即PB2＝PD2＋BD2，所以PD⊥BD.‎ 又因为DE，BD⊂平面BCED，DE∩BD＝D，所以PD⊥平面BCED.‎ 又因为PD⊂平面PDE，所以平面PDE⊥平面BCED.‎ ‎(2)由(1)可知，BD⊥DE，PD⊥平面BCED，如图所示，以D为原点，DB，DE，DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系，则B(1，0，0)，E，P(0，0，1)，C，所以＝，＝.‎ 设n＝(x0，y0，z0)为平面PCE的法向量，‎ 所以令y0＝，则x0＝－1，z0＝1，即n＝(－1，，1)．又＝(1，0，－1)，‎ 所以|cos〈，n〉|＝＝＝.‎ 设直线PB与平面PCE所成的角为θ，则sin θ＝.‎ 即直线PB与平面PCE所成角的正弦值为.‎ ‎4．解：(1)设从“健身达人”中随机抽取的2人中，去年的消费金额超过4 000元的消费者有X位，则X的可能值为0，1，2.‎ 方法一：P(X≥1)＝P(X＝1)＋P(X＝2)＝＋＝＋＝.‎ 方法二：P(X≥1)＝1－P(X＝0)＝1－＝.‎ 故至少有1位消费者去年的消费金额超过4 000元的概率为.‎ ‎(2)方案1：按分层抽样从普通会员、银卡会员、金卡会员中总共抽取25位“幸运之星”，则“幸运之星”中的普通会员、银卡会员、金卡会员的人数分别为×25＝7，×25＝15，×25＝3，‎ 所以按照方案1奖励的总金额 ξ1＝7×500＋15×600＋3×800＝14 900(元)．‎ 方案2：设η表示参加一次摸奖游戏所获得的奖励金，‎ 则η的可能值为0，200，300.‎ 因为摸球1次，摸到红球的概率为＝，摸到白球的概率为＝，‎ 所以P(η＝0)＝C＋C＝，‎ P(η＝200)＝C＝，‎ P(η＝300)＝C＝，‎ 所以η的分布列为 η ‎0‎ ‎200‎ ‎300‎ P 所以E(η)＝0×＋200×＋300×＝76.8(元)，‎ 所以按照方案2奖励的总金额 ξ2＝(28＋2×60＋3×12)×76.8＝14 131.2(元)．‎ 因为方案1奖励的总金额ξ1多于方案2奖励的总金额ξ2，‎ 所以预测方案2投资较少．‎