2013版高考数学二轮复习专题训练：立体几何 9页

‎2013版高考数学二轮复习专题训练：立体几何 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．‎ 第Ⅰ卷(选择题　共60分)‎ 一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．若一个棱锥的各棱长均相等，则该棱锥一定不是( )‎ A．三棱锥 B．四棱锥 C．五棱锥 D．六棱锥 ‎【答案】D ‎2．已知空间四边形ABCD的每条边和对角线的长都等于，点E、F分别是边BC、AD的中点，则的值为( )‎ A． B． C． D．‎ ‎【答案】C ‎3．一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:①三角形;②矩形;③正方形;④正六边形.其中正确的结论有( )‎ A．①②③ B．②③④ C．①②④ D．①③④‎ ‎【答案】B ‎4．点是等腰三角形所在平面外一点，中，底边的距离为( )‎ A． B． C． D．‎ ‎【答案】A ‎5．—个几何体的正视图与侧视图相同，均为下图所示，则其俯视图可能是( )‎ ‎ ‎ ‎【答案】B ‎6．如图，已知四棱锥 V-ABCD的底面是边长为2正方形，侧面都是侧棱长为的等腰三角形，则二面角V-AB-C的大小为（ ）‎ A．30° B．45° C．60° D．90°‎ ‎【答案】C ‎7．若用一个平面去截一个正方体得到一个截面多边形,则该多边形不可能是( )‎ A．锐角三角形 B．直角三角形 C．菱形 D．正六边形 ‎【答案】B ‎8．空间三条直线中的一条直线与其他两条都相交，那么由这三条直线最多可确定平面的个数是( )个 A．1 B．‎2 ‎C． 3 D．4‎ ‎【答案】C ‎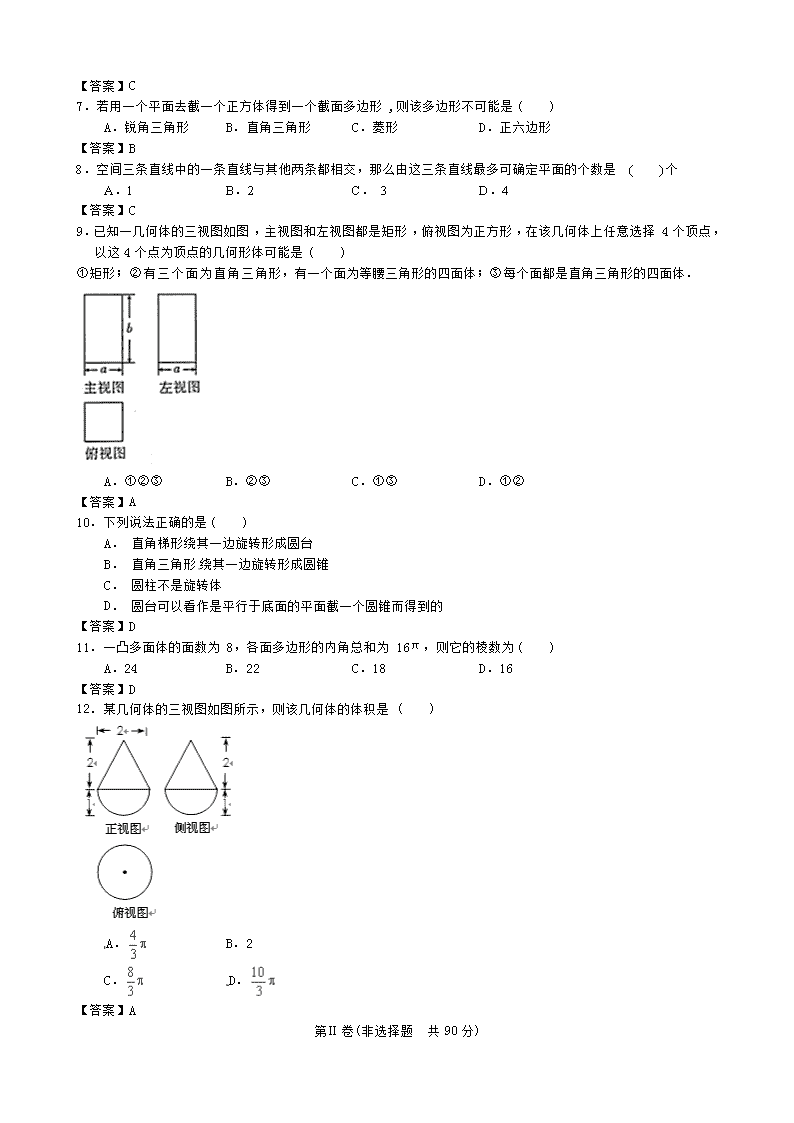9．已知一几何体的三视图如图，主视图和左视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，以这4个点为顶点的几何形体可能是( )‎ ‎①矩形；②有三个面为直角三角形，有一个面为等腰三角形的四面体；③每个面都是直角三角形的四面体．‎ A．①②③ B．②③ C．①③ D．①②‎ ‎【答案】A ‎10．下列说法正确的是( )‎ A． 直角梯形绕其一边旋转形成圆台 B． 直角三角形绕其一边旋转形成圆锥 C． 圆柱不是旋转体 D． 圆台可以看作是平行于底面的平面截一个圆锥而得到的 ‎【答案】D ‎11．一凸多面体的面数为8，各面多边形的内角总和为16π，则它的棱数为( )‎ A．24 B．‎22 ‎C．18 D．16‎ ‎【答案】D ‎12．某几何体的三视图如图所示，则该几何体的体积是( )‎ A． B．2 ‎ C． D．‎ ‎【答案】A 第Ⅱ卷(非选择题　共90分)‎ 二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)‎ ‎13．已知，，，若、、共同作用于一个物体上，使物体从点（1，-2，1）移到点（3，1，-2），则合力所做的功为 .‎ ‎【答案】4‎ ‎14．如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为 .‎ ‎【答案】‎ ‎15．正方体AC1中，过点A作截面，使正方体的12条棱所在直线与截面所成的角都相等，试写出满足条件的一个截面____________‎ ‎【答案】面AD‎1C ‎16．在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是                   (写出所有正确结论的编号）.‎ ‎①矩形；‎ ‎②不是矩形的平行四边形；‎ ‎③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；‎ ‎④每个面都是等边三角形的四面体；‎ ‎⑤每个面都是直角三角形的四面体.‎ ‎【答案】①③④⑤‎ 三、解答题 (本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)‎ ‎17．如图所示，在直三棱柱ABC－A1B‎1C1中，AB＝BB1＝BC，AC1⊥平面A1BD，D为AC的中点．‎ ‎(1)求证：B‎1C∥平面A1BD；‎ ‎(2)求证：B‎1C1⊥平面ABB‎1A1；‎ ‎(3)在CC1上是否存在一点E，使得∠BA1E＝45°，若存在，试确定E的位置，并判断平面A1BD与平面BDE是否垂直？若不存在，请说明理由．‎ ‎【答案】(1)连结AB1与A1B相交于M，则M为A1B的中点．连结MD，又D为AC的中点，‎ ‎∴B‎1C∥MD，‎ 又B‎1C⊄平面A1BD，MD⊂平面A1BD，∴B‎1C∥平面A1BD.‎ ‎(2)∵AB＝B1B，∴平行四边形ABB‎1A1为正方形，‎ ‎∴A1B⊥AB1.又∵AC1⊥平面A1BD，‎ ‎∴AC1⊥A1B，∴A1B⊥平面AB‎1C1，∴A1B⊥B‎1C1.‎ 又在直三棱柱ABC－A1B‎1C1中，BB1⊥B‎1C1，‎ ‎∴B‎1C1⊥平面ABB‎1A1.‎ ‎(3)设AB＝a，CE＝x，∵B‎1C1⊥A1B1，在Rt△A1B‎1C1中有A‎1C1＝a，同理A1B1＝a，‎ ‎∴C1E＝a－x，‎ ‎∴A1E＝＝，BE＝，‎ ‎∴在△A1BE中，由余弦定理得 BE2＝A1B2＋A1E2－‎2A1B·A1E·cos45°，即 a2＋x2＝‎2a2＋x2＋‎3a2－2ax－‎2‎a·，‎ ‎∴＝‎2a－x，‎ ‎∴x＝a，即E是C‎1C的中点，‎ ‎∵D、E分别为AC、C‎1C的中点，∴DE⊥AC1.‎ ‎∵AC1⊥平面A1BD，∴DE⊥平面A1BD.‎ 又DE⊂平面BDE，∴平面A1BD⊥平面BDE.‎ ‎18．如图，在四棱锥A-ABCD中，底面ABCD是正方形，其他四个侧面都是等边三角形，AC与BD的交点为O，E为侧棱SC上一点. ‎ ‎(1）当E为侧棱SC的中点时，求证：SA∥平面BDE；‎ ‎(2）求证：平面BDE⊥平面SAC；‎ ‎(3）当二面角E-BD-C的大小为45°时，‎ 试判断点E在SC上的位置，并说明理由.‎ ‎【答案】（Ⅰ）连接，由条件可得∥.‎ ‎ 因为平面，平面，‎ ‎ 所以∥平面. ‎ ‎(Ⅱ）法一：证明：由已知可得，,是中点，‎ 所以，‎ 又因为四边形是正方形，所以.‎ 因为，所以.‎ 又因为，所以平面平面. -‎ ‎(Ⅱ）法二：证明：由（Ⅰ）知，.‎ 建立如图所示的空间直角坐标系.‎ 设四棱锥的底面边长为2，‎ 则，，，‎ ‎，，.‎ 所以，.‎ 设（），由已知可求得.‎ 所以，.‎ 设平面法向量为， ‎ 则 即 ‎ 令，得. ‎ 易知是平面的法向量.‎ 因为，‎ 所以，所以平面平面. ‎ ‎(Ⅲ）设（），由（Ⅱ）可知，‎ 平面法向量为.‎ 因为，‎ 所以是平面的一个法向量.‎ 由已知二面角的大小为.‎ 所以，‎ 所以，解得.‎ 所以点是的中点. ‎ ‎19．如图，在三棱拄中，侧面，已知 ‎(1）求证：；‎ ‎ (2）、当为的中点时，求二面角的平面角的正切值.‎ ‎【答案】（1）因为侧面，故 在中，由余弦定理有 ‎ ‎ 故有 而 且平面 ‎ ‎(2）取的中点，的中点，的中点，的中点， 连则，连则，连则 连则，且为矩形，‎ 又 故为所求二面角的平面角在中，‎ ‎ ‎ ‎ (法二： 建系：由已知， 所以二面角的平面角的大小为向量与的夹角因为 ‎ 故 ）‎ ‎20．如图，四棱锥P—ABCD中，PD⊥平面ABCD，底面ABCD为矩形，PD=DC=4，AD=2，E为PC的中点.‎ ‎(I）求证：AD⊥PC；‎ ‎(II）求三棱锥P-ADE的体积；‎ ‎(III）在线段AC上是否存在一点M，使得PA//平面EDM，若存在，求出AM的长；若不存在，请说明理由.‎ ‎【答案】（I）因为PD⊥平面ABCD.‎ ‎ 所以PD⊥AD.‎ ‎ 又因为ABCD是矩形，‎ ‎ 所以AD⊥CD.‎ ‎ 因为 ‎ 所以AD⊥平面PCD.‎ ‎ 又因为平面PCD，‎ ‎ 所以AD⊥PC.‎ ‎(II）因为AD⊥平面PCD，VP-ADE=VA-PDE，‎ ‎ 所以AD是三棱锥A—PDE的高.‎ 因为E为PC的中点，且PD=DC=4，‎ 所以 又AD=2，‎ 所以 ‎(III）取AC中点M，连结EM、DM，‎ ‎ 因为E为PC的中点，M是AC的中点，‎ 所以EM//PA，‎ 又因为EM平面EDM，PA平面EDM，‎ 所以PA//平面EDM.‎ 所以 即在AC边上存在一点M，使得PA//平面EDM，AM的长为.‎ ‎21．如图，直三棱柱，，，点分别为和的中点 ‎(1）证明：；‎ ‎(2）若二面角为直二面角，求的值 ‎【答案】（1）连结，由已知 三棱柱为直三棱柱，‎ 所以为中点.又因为为中点 所以，又平面 ‎ 平面，因此 ‎ ‎(2）以为坐标原点，分别以直线为轴，轴，轴建立直角坐标系，如图所示 设则，‎ 于是，‎ 所以，设是平面的法向量，‎ 由得，可取 设是平面的法向量，‎ 由得，可取 因为为直二面角，所以，解得 ‎22．如图，在四棱锥P－ABCD中，PA⊥底面ABCD，且底面ABCD是正方形，DM⊥PC，垂足为M.‎ ‎(1）求证：BD⊥平面PAC．‎ ‎(2）求证：平面MBD⊥平面PCD． ‎ ‎【答案】（1）连结AC，‎ ‎∵底面ABCD是正方形 ‎∴BD⊥AC，‎ ‎∵PA⊥底面ABCD，‎ BD⊂平面ABCD，‎ ‎∴PA⊥BD，‎ ‎∵PA AC=A ‎ ‎∴BD⊥平面PAC．‎ ‎ (2）由（1）知BD⊥平面PAC ‎ ‎∵PC⊂平面PAC ‎∴BD⊥PC ‎ ‎∵DM⊥PC BD DM=D ‎ ‎∴PC⊥平面DBM ‎ ‎∵PC⊂平面PDC，‎ ‎∴平面MBD⊥平面PCD. ‎