高中数学人教a版必修四课时训练：1.4.3 正切函数的性质与图象 5页

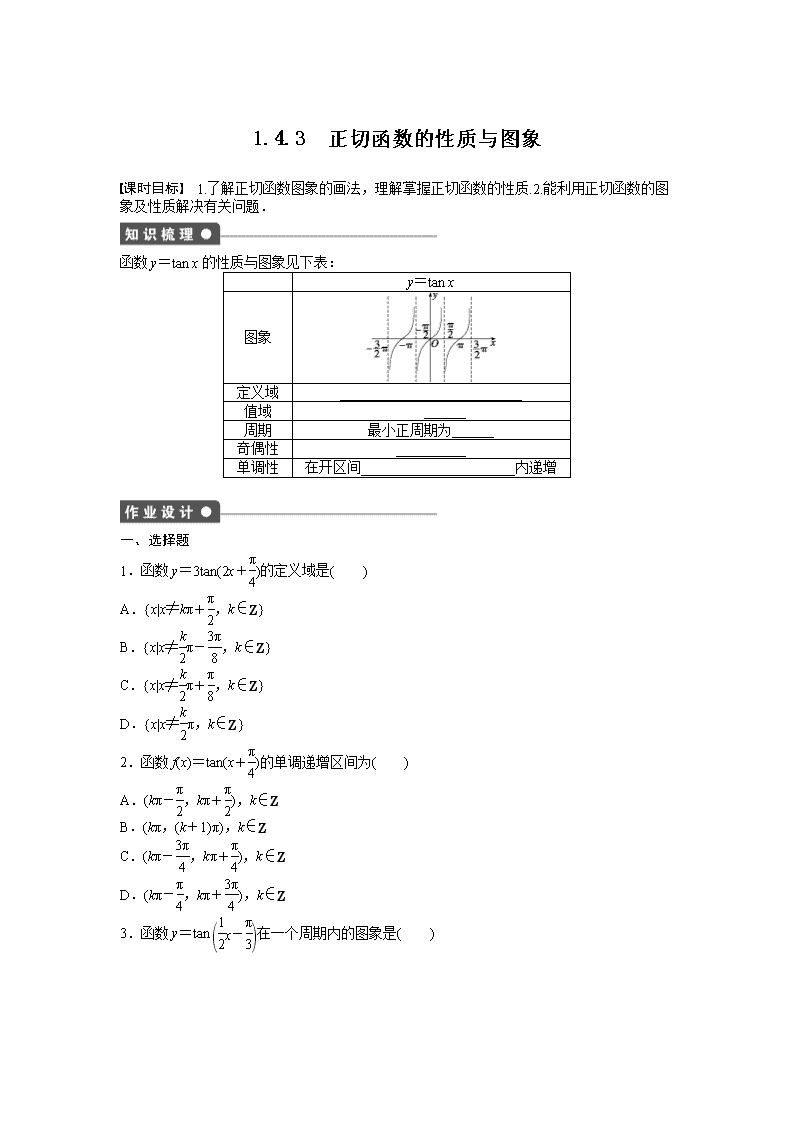
1.4.3 正切函数的性质与图象 课时目标 1.了解正切函数图象的画法，理解掌握正切函数的性质.2.能利用正切函数的图 象及性质解决有关问题． 函数 y＝tan x 的性质与图象见下表： y＝tan x 图象 定义域 __________________________ 值域 ______ 周期 最小正周期为______ 奇偶性 __________ 单调性 在开区间______________________内递增 一、选择题 1．函数 y＝3tan(2x＋π 4)的定义域是( ) A．{x|x≠kπ＋π 2 ，k∈Z} B．{x|x≠k 2π－3π 8 ，k∈Z} C．{x|x≠k 2π＋π 8 ，k∈Z} D．{x|x≠k 2π，k∈Z} 2．函数 f(x)＝tan(x＋π 4)的单调递增区间为( ) A．(kπ－π 2 ，kπ＋π 2)，k∈Z B．(kπ，(k＋1)π)，k∈Z C．(kπ－3π 4 ，kπ＋π 4)，k∈Z D．(kπ－π 4 ，kπ＋3π 4 )，k∈Z 3．函数 y＝tan 1 2x－π 3 在一个周期内的图象是( ) 4．下列函数中，在 0，π 2 上单调递增，且以π为周期的偶函数是( ) A．y＝tan|x| B．y＝|tan x| C．y＝|sin 2x| D．y＝cos 2x 5．下列各式中正确的是( ) A．tan 735°>tan 800° B．tan 1>－tan 2 C．tan 5π 7 0)的图象的相邻两支截直线 y＝π 4 所得线段长为π 4 ，则 f π 4 的值是( ) A．0 B．1 C．－1 D.π 4 题 号 1 2 3 4 5 6 答 案 二、填空题 7．函数 y＝ tan x－1的定义域是____________． 8．函数 y＝3tan(ωx＋π 6)的最小正周期是π 2 ，则ω＝____. 9．已知 a＝tan 1，b＝tan 2，c＝tan 3，则 a，b，c 按从小到大的排列是________________． 10．函数 y＝3tan x＋π 3 的对称中心的坐标是_________________________________． 三、解答题 11．判断函数 f(x)＝lg tan x＋1 tan x－1 的奇偶性． 12．求函数 y＝tan x 2 －π 3 的定义域、周期、单调区间和对称中心． 能力提升 13．函数 y＝tan x＋sin x－|tan x－sin x|在区间 π 2 ，3π 2 内的图象是( ) 14．已知函数 y＝tan ωx 在(－π 2 ，π 2)内是减函数，则( ) A．0<ω≤1 B．－1≤ω<0 C．ω≥1 D．ω≤－1 1．正切函数 y＝tan x 在每段区间 kπ－π 2 ，kπ＋π 2 (k∈Z)上是单调递增函数，但不能说正切 函数在其定义域内是单调递增函数．并且每个单调区间均为开区间，而不能写成闭区间 －π 2 ＋kπ，π 2 ＋kπ (k∈Z)．正切函数无单调减区间． 2．正切函数是奇函数，图象关于原点对称，且有无穷多个对称中心，对称中心坐标是(kπ 2 ， 0) (k∈Z)．正切函数的图象无对称轴，但图象以直线 x＝kπ＋π 2 (k∈Z)为渐近线． 1．4.3 正切函数的性质与图象 答案 知识梳理 {x|x∈R，且 x≠kπ＋π 2 ，k∈Z} R π 奇函数 kπ－π 2 ，kπ＋π 2 (k∈Z) 作业设计 1．C 2.C 3.A 4.B 5.D 6．A [由题意，T＝π ω ＝π 4 ，∴ω＝4. ∴f(x)＝tan 4x，f π 4 ＝tan π＝0.] 7．[kπ＋π 4 ，kπ＋π 2)，k∈Z. 8．±2 解析 T＝ π |ω| ＝π 2 ，∴ω＝±2. 9．b0，得 tan x>1 或 tan x<－1. ∴函数定义域为 kπ－π 2 ，kπ－π 4 ∪ kπ＋π 4 ，kπ＋π 2 (k∈Z) 关于原点对称． f(－x)＋f(x)＝lg tan－x＋1 tan－x－1 ＋lg tan x＋1 tan x－1 ＝lg －tan x＋1 －tan x－1 ·tan x＋1 tan x－1 ＝lg 1＝0. ∴f(－x)＝－f(x)， ∴f(x)是奇函数． 12．解 ①由x 2 －π 3 ≠kπ＋π 2 ，k∈Z， 得 x≠2kπ＋5 3π，k∈Z. ∴函数的定义域为 x|x∈R 且 x≠2kπ＋5 3π，k∈Z . ②T＝π 1 2 ＝2π，∴函数的周期为 2π. ③由 kπ－π 2sin x，y＝2sin x．故选 D.] 14．B [∵y＝tan ωx 在(－π 2 ，π 2)内是减函数， ∴ω<0 且 T＝ π |ω| ≥π. ∴|ω|≤1，即－1≤ω<0.]