【数学】2019届高考一轮复习北师大版理9-1直线的倾斜角与斜率、直线的方程学案 14页

知识点 考纲下载 直线的方程 ‎ 在平面直角坐标系中，结合具体图形，确定直线位置的几何要素．‎ ‎ 理解直线的倾斜角和斜率的概念，掌握过两点的直线斜率的计算公式．‎ ‎ 掌握确定直线位置的几何要素，掌握直线方程的几种形式(点斜式、两点式及一般式)，了解斜截式与一次函数的关系.‎ 两直线的位置关系 ‎ 能根据两条直线的斜率判定这两条直线平行或垂直．‎ ‎ 能用解方程组的方法求两条相交直线的交点坐标．‎ ‎ 掌握两点间的距离公式、点到直线的距离公式，会求两条平行直线间的距离.‎ 圆的方程 掌握确定圆的几何要素，掌握圆的标准方程与一般方程.‎ 直线、圆的位置关系 ‎ 能根据给定直线、圆的方程判断直线与圆的位置关系；能根据给定两个圆的方程判断两圆的位置关系．‎ ‎ 能用直线和圆的方程解决一些简单的问题．‎ ‎ 初步了解用代数方法处理几何问题的思想.‎ 椭 圆 ‎ 了解圆锥曲线的实际背景，了解圆锥曲线在刻画现实世界和解决实际问题中的作用．‎ ‎ 掌握椭圆的定义、几何图形、标准方程及简单性质.‎ 双曲线 了解双曲线的定义、几何图形和标准方程，知道它的简单几何性质.‎ 抛物线 掌握抛物线的定义、几何图形、标准方程及简单性质.‎ 曲线与方程 了解方程的曲线与曲线的方程的对应关系．理解数形结合的思想，了解圆锥曲线的简单应用.‎ 第1讲　直线的倾斜角与斜率、直线的方程 ‎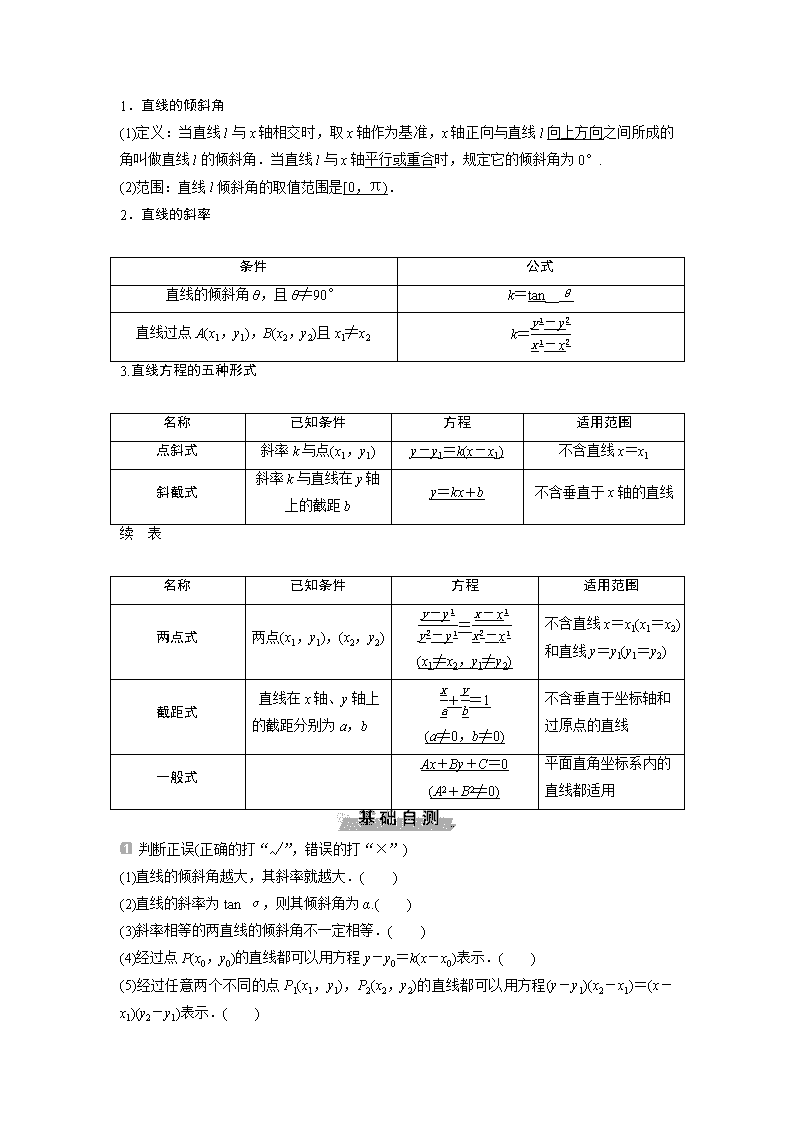1．直线的倾斜角 ‎(1)定义：当直线l与x轴相交时，取x轴作为基准，x轴正向与直线l向上方向之间所成的角叫做直线l的倾斜角．当直线l与x轴平行或重合时，规定它的倾斜角为0°.‎ ‎(2)范围：直线l倾斜角的取值范围是[0，π)．‎ ‎2．直线的斜率 条件 公式 直线的倾斜角θ，且θ≠90°‎ k＝tan__θ 直线过点A(x1，y1)，B(x2，y2)且x1≠x2‎ k＝ ‎3.直线方程的五种形式 名称 已知条件 方程 适用范围 点斜式 斜率k与点(x1，y1)‎ y－y1＝k(x－x1)‎ 不含直线x＝x1‎ 斜截式 斜率k与直线在y轴上的截距b y＝kx＋b 不含垂直于x轴的直线 续　表 名称 已知条件 方程 适用范围 两点式 两点(x1，y1)，(x2，y2)‎ ＝ ‎(x1≠x2，y1≠y2)‎ 不含直线x＝x1(x1＝x2)和直线y＝y1(y1＝y2)‎ 截距式 ‎ 直线在x轴、y轴上的截距分别为a，b ＋＝1‎ ‎(a≠0，b≠0)‎ 不含垂直于坐标轴和过原点的直线 一般式 Ax＋By＋C＝0‎ ‎(A2＋B2≠0)‎ 平面直角坐标系内的直线都适用 ‎ 判断正误(正确的打“√”，错误的打“×”)‎ ‎(1)直线的倾斜角越大，其斜率就越大．(　　)‎ ‎(2)直线的斜率为tan α，则其倾斜角为α.(　　)‎ ‎(3)斜率相等的两直线的倾斜角不一定相等．(　　)‎ ‎(4)经过点P(x0，y0)的直线都可以用方程y－y0＝k(x－x0)表示．(　　)‎ ‎(5)经过任意两个不同的点P1(x1，y1)，P2(x2，y2)的直线都可以用方程(y－y1)(x2－x1)＝(x－x1)(y2－y1)表示．(　　)‎ 答案：(1)×　(2)×　(3)×　(4)×　(5)√‎ ‎ (教材习题改编)经过点P0(2，－3)，倾斜角为45°的直线方程为(　　)‎ A．x＋y＋1＝0　　　　　　 B．x＋y－1＝0‎ C．x－y＋5＝0 D．x－y－5＝0‎ 解析：选D.由点斜式得直线方程为 y－(－3)＝tan 45°(x－2)＝x－2，‎ 即x－y－5＝0，故选D.‎ ‎ 如果AC＜0，BC＜0，那么直线Ax＋By＋C＝0不通过(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 解析：选C.由题意知直线的斜率k＝－＜0，直线在y轴上的截距b＝－＞0，故选C.‎ ‎ 经过两点A(4，2y＋1)，B(2，－3)的直线的倾斜角为，则y＝________．‎ 解析：tan ＝＝＝y＋2，‎ 因此y＋2＝－1，y＝－3.‎ 答案：－3‎ ‎ (教材习题改编)经过点(－4，3)且在两坐标轴上的截距相等且不过原点的直线方程为________．‎ 解析：由题意可设方程为x＋y＝a，‎ 所以a＝－4＋3＝－1.‎ 所以直线方程为x＋y＋1＝0.‎ 答案：x＋y＋1＝0‎ ‎　　　　　　直线的倾斜角与斜率 ‎ [典例引领]‎ ‎ (1)直线2xcos α－y－3＝0的倾斜角的变化范围是(　　)‎ A.　　　　　　　　 B. C. D. ‎(2)已知直线l：x－my＋m＝0上存在点M满足与两点A(－1，0)，B(1，0)连线的斜率kMA与kMB之积为3，则实数m的取值范围是(　　)‎ A．[－， ]‎ B.∪ C.∪ D．以上都不对 ‎【解析】　(1)直线2xcos α－y－3＝0的斜率k＝2cos α.由于α∈，所以≤cos α≤，因此k＝2cos α∈[1，]．设直线的倾斜角为θ，则有tan θ∈[1，]．由于θ∈[0，π)，所以θ∈，即倾斜角的变化范围是.‎ ‎(2)设M(x，y)，由kMA·kMB＝3，得·＝3，即y2＝3x2－3.‎ 联立得x2＋x＋6＝0.‎ 要使直线l：x－my＋m＝0上存在点M满足与两点A(－1，0)，B(1，0)连线的斜率kMA与kMB之积为3，则Δ＝－24≥0，即m2≥.所以实数m的取值范围是∪.故选C.‎ ‎【答案】　(1)B　(2)C 若本例(1)中直线变为x＋ycos θ－3＝0(θ∈R)，则直线的倾斜角α的取值范围为________．‎ 解析：当cos θ＝0时，方程变为x－3＝0，其倾斜角为；‎ 当cos θ≠0时，由直线l的方程，可得斜率k＝－.‎ 因为cos θ∈[－1，1]且cos θ≠0，‎ 所以k∈(－∞，－1]∪[1，＋∞)，‎ 即tan α∈(－∞，－1]∪[1，＋∞)，‎ 又α∈[0，π)，所以α∈∪，‎ 综上知，直线l的倾斜角α的取值范围是.‎ 答案： ‎(1)求倾斜角的取值范围的一般步骤 ‎①求出斜率k＝tan α的取值范围．‎ ‎②利用三角函数的单调性，借助图象，确定倾斜角α的取值范围．‎ 求倾斜角时要注意斜率是否存在．‎ ‎(2)斜率的求法 ‎①定义法：若已知直线的倾斜角α或α的某种三角函数值，一般根据k＝tan α求斜率．‎ ‎②公式法：若已知直线上两点A(x1，y1)，B(x2，y2)，一般根据斜率公式k＝(x1≠x2)求斜率．　 ‎ ‎[通关练习]‎ ‎1．若直线l的斜率为k，倾斜角为α，且α∈∪，则k的取值范围是________．‎ 解析：当α∈时，k＝tan α∈；‎ 当α∈时，k＝tan α∈[－，0)．‎ 综上k∈[－，0)∪.‎ 答案：[－，0)∪ ‎2．曲线y＝x3－x＋5上各点处的切线的倾斜角的取值范围为________．‎ 解析：记曲线上点P处的切线的倾斜角是θ，‎ 因为y′＝3x2－1≥－1，‎ 所以tan θ≥－1，‎ 所以θ为钝角时，应有θ∈；‎ θ为锐角时，tan θ≥－1显然成立．‎ 综上，θ的取值范围是∪.‎ 答案：∪ ‎　　　　　　求直线的方程 ‎ [典例引领]‎ ‎ 根据所给条件求直线的方程：‎ ‎(1)直线过点(－4，0)，倾斜角的正弦值为；‎ ‎(2)经过点P(4，1)，且在两坐标轴上的截距相等；‎ ‎(3)(待定系数法)直线过点(5，10)，到原点的距离为5.‎ ‎【解】　(1)由题设知，该直线的斜率存在，故可采用点斜式．‎ 设倾斜角为α，则sin α＝(0＜α＜π)，‎ 从而cos α＝±，‎ 则k＝tan α＝±.‎ 故所求直线方程为y＝±(x＋4)．‎ 即x＋3y＋4＝0或x－3y＋4＝0.‎ ‎(2)设直线l在x，y轴上的截距均为a，‎ 若a＝0，即l过点(0，0)及(4，1)，‎ 所以l的方程为y＝x，即x－4y＝0.‎ 若a≠0，则设l的方程为＋＝1，‎ 因为l过点(4，1)，所以＋＝1，‎ 所以a＝5，‎ 所以l的方程为x＋y－5＝0.‎ 综上可知，直线l的方程为x－4y＝0或x＋y－5＝0.‎ ‎(3)当斜率不存在时，所求直线方程为x－5＝0，当斜率存在时，设其为k，则所求直线方程为y－10＝k(x－5)，‎ 即kx－y＋(10－5k)＝0.‎ 由点到直线的距离公式，得＝5，‎ 解得k＝.‎ 故所求直线方程为3x－4y＋25＝0.‎ 综上知，所求直线方程为x－5＝0或3x－4y＋25＝0.‎ ‎(1)求直线方程的两种常用方法 ‎①直接法：根据已知条件，确定适当的直线方程形式，直接写出直线方程；‎ ‎②待定系数法：先设出直线方程，再根据已知条件求出待定的系数，最后代入求出直线的方程．‎ ‎(2)求直线方程应注意的问题 ‎①选择直线方程时，应注意分类讨论思想的应用：选用点斜式或斜截式时，需讨论直线的斜率是否存在；选用截距式时，需讨论直线是否过原点．‎ ‎②求直线方程时，如果没有特别要求，求出的方程应化为一般式Ax＋By＋C＝0(A，B不同时为0)．　 ‎ ‎[通关练习]‎ ‎1．已知A(－1，1)，B(3，1)，C(1，3)，则△ABC的BC边上的高所在直线方程为(　　)‎ A．x＋y＝0　　　　　　 B．x－y＋2＝0‎ C．x＋y＋2＝0 D．x－y＝0‎ 解析：选B.因为B(3，1)，C(1，3)，‎ 所以kBC＝＝－1，‎ 故BC边上的高所在直线的斜率k＝1，‎ 又高线经过点A，‎ 所以其直线方程为x－y＋2＝0.‎ ‎2．过点M(－1，－2)作一条直线l，使得l夹在两坐标轴之间的线段被点M平分，则直线l的方程为________．‎ 解析：由题意，可设所求直线l的方程为y＋2＝k(x＋1)(k≠0)，直线l与x轴、y轴分别交于A、B两点，则A，B(0，k－2)．因为AB的中点为M，所以解得k＝－2.所以所求直线l的方程为2x＋y＋4＝0.‎ 答案：2x＋y＋4＝0‎ ‎　　　　　　直线方程的综合应用(高频考点)‎ 直线方程的综合应用是解析几何的一个基础内容，在高考中常与其他知识结合考查，多以选择题、填空题的形式呈现，难度为中、低档题目．高考中对直线方程的综合应用考查主要有以下两个命题角度：‎ ‎(1)与基本不等式相结合求最值问题；‎ ‎(2)由直线方程解决参数问题．‎ ‎ [典例引领]‎ ‎ 角度一　与基本不等式相结合求最值问题 ‎ 直线l过点P(1，4)，分别交x轴的正半轴和y轴的正半轴于A、B两点，O为坐标原点，当|OA|＋|OB|最小时，求l的方程．‎ ‎【解】　依题意，l的斜率存在，且斜率为负，‎ 设直线l的斜率为k，‎ 则直线l的方程为y－4＝k(x－1)(k<0)．‎ 令y＝0，可得A；‎ 令x＝0，可得B(0，4－k)．‎ ‎|OA|＋|OB|＝＋(4－k)＝5－ ‎＝5＋≥5＋4＝9.‎ 所以当且仅当－k＝且k<0，‎ 即k＝－2时，|OA|＋|OB|取最小值．‎ 这时l的方程为2x＋y－6＝0.‎ 角度二　由直线方程解决参数问题 ‎ 已知直线l1：ax－2y＝2a－4，l2：2x＋a2y＝2a2＋4，当0＜a＜2时，直线l1，l2与两坐标轴围成一个四边形，当四边形的面积最小时，求实数a的值．‎ ‎【解】　由题意知直线l1，l2恒过定点P(2，2)，直线l1在y轴上的截距为2－a，直线l2在x轴上的截距为a2＋2，‎ 所以四边形的面积S＝×2×(2－a)＋×2×(a2＋2)＝a2－a＋4＝＋，‎ 当a＝时，面积最小．‎ 直线方程综合问题的两大类型及其解法 ‎(1)求解与直线方程有关的最值问题．先设出直线方程，建立目标函数，再利用基本不等式求解最值．‎ ‎(2)求参数值或范围．注意点在直线上，则点的坐标适合直线的方程，再结合函数的单调性或基本不等式求解．　 ‎ ‎[通关练习]‎ ‎1．直线x－2y＋b＝0与两坐标轴所围成的三角形的面积不大于1，那么b的取值范围是(　　)‎ A．[－2，2]　　　　　　　 ‎ B．(－∞，－2]∪[2，＋∞)‎ C．[－2，0)∪(0，2] ‎ D．(－∞，＋∞)‎ 解析：选C.令x＝0，得y＝，令y＝0，得x＝－b，‎ 所以所求三角形的面积为|－b|＝b2，且b≠0，b2≤1，所以b2≤4，所以b的取值范围是[－2，0)∪(0，2]．‎ ‎2．已知直线x＋2y＝2分别与x轴、y轴相交于A，B两点，若动点P(a，b)在线段AB上，则ab的最大值为________．‎ 解析：直线方程可化为＋y＝1，故直线与x轴的交点为A(2，0)，与y轴的交点为B(0，1)，由动点P(a，b)在线段AB上，可知0≤b≤1，且a＋2b＝2，从而a＝2－2b，故ab＝(2－2b)b＝－2b2＋2b＝－2＋，由于0≤b≤1，故当b＝时，ab取得最大值.‎ 答案： ‎ 直线的倾斜角和斜率的关系 ‎(1)任何直线都存在倾斜角，但并不是任意直线都存在斜率．‎ ‎(2)直线的倾斜角α和斜率k之间的对应关系：‎ α ‎0°‎ ‎0°＜α＜90°‎ ‎90°‎ ‎90°＜α＜180°‎ k ‎0‎ k＞0‎ 不存在 k＜0‎ ‎ 求直线方程的一般方法 ‎(1)直接法：根据已知条件，选择适当的直线方程形式，直接写出直线方程，选择时，应注意各种形式的方程的适用范围，必要时要分类讨论．‎ ‎(2)待定系数法，具体步骤为：‎ ‎①设所求直线方程的某种形式；‎ ‎②由条件建立所求参数的方程(组)；‎ ‎③解这个方程(组)求出参数；‎ ‎④把参数的值代入所设直线方程．‎ ‎ 易错防范 ‎(1)求直线方程时要注意判断直线斜率是否存在；每条直线都有倾斜角，但不一定每条直线都存在斜率．‎ ‎(2)根据斜率求倾斜角，要注意倾斜角的范围．‎ ‎(3)直线的截距式中易忽视截距均不为0这一条件，当截距为0时可用点斜式．‎ ‎(4)由一般式Ax＋By＋C＝0确定斜率k时易忽视判断B是否为0，当B＝0时，k不存在；当B≠0时，k＝－.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ‎ ‎1．(2018·大连模拟)倾斜角为120°，在x轴上的截距为－1的直线方程是(　　)‎ A.x－y＋1＝0　　　　　 B.x－y－＝0‎ C.x＋y－＝0 D.x＋y＋＝0‎ 解析：选D.由于倾斜角为120°，故斜率k＝－.又直线过点(－1，0)，所以方程为y＝－(x＋1)，即x＋y＋＝0.‎ ‎2．已知直线l的斜率为，在y轴上的截距为另一条直线x－2y－4＝0的斜率的倒数，则直线l的方程为(　　)‎ A．y＝x＋2 B．y＝x－2‎ C．y＝x＋ D．y＝－x＋2‎ 解析：选A.因为直线x－2y－4＝0的斜率为，‎ 所以直线l在y轴上的截距为2，‎ 所以直线l的方程为y＝x＋2.‎ ‎3．直线l经过点A(1，2)，在x轴上的截距的取值范围是(－3，3)，则其斜率的取值范围是(　　)‎ A．－1＜k＜ B．k＞1或k＜ C．k＞或k＜1 D．k＞或k＜－1‎ 解析：选D.设直线的斜率为k，则直线方程为y－2＝k(x－1)，‎ 令y＝0，得直线l在x轴上的截距为1－，‎ 则－3＜1－＜3，解得k＞或k＜－1.‎ ‎4．已知函数f(x)＝ax(a＞0且a≠1)，当x＜0时，f(x)＞1，方程y＝ax＋表示的直线是(　　)‎ 解析：选C.因为x＜0时，ax＞1，所以0＜a＜1.‎ 则直线y＝ax＋的斜率0＜a＜1，‎ 在y轴上的截距＞1.故选C.‎ ‎5．(2018·太原质检)若直线l与直线y＝1，x＝7分别交于点P，Q，且线段PQ的中点坐标为(1，－1)，则直线l的斜率为(　　)‎ A. B．－ C．－ D. 解析：选B.依题意，设点P(a，1)，Q(7，b)，则有解得a＝－5，b＝－3，从而可知直线l的斜率为＝－.‎ ‎6．过点A(－1，－3)，斜率是直线y＝3x的斜率的－的直线方程为________．‎ 解析：设所求直线的斜率为k，依题意 k＝－×3＝－.‎ 又直线经过点A(－1，－3)，‎ 因此所求直线方程为y＋3＝－(x＋1)，‎ 即3x＋4y＋15＝0.‎ 答案：3x＋4y＋15＝0‎ ‎7．设点A(－1，0)，B(1，0)，直线2x＋y－b＝0与线段AB相交，则b的取值范围是________．‎ 解析：b为直线y＝－2x＋b在y轴上的截距，如图，‎ 当直线y＝－2x＋b过点A(－1，0)和点B(1，0)时，b分别取得最小值和最大值．‎ 所以b的取值范围是[－2，2]．‎ 答案：[－2，2]‎ ‎8．一条直线经过点A(－2，2)，并且与两坐标轴围成的三角形的面积为1，则此直线的方程为________________．‎ 解析：设所求直线的方程为＋＝1，‎ 因为A(－2，2)在直线上，所以－＋＝1.①‎ 又因为直线与坐标轴围成的三角形面积为1，‎ 所以|a|·|b|＝1.②‎ 由①②可得(1)或(2) 由(1)解得或方程组(2)无解．‎ 故所求的直线方程为＋＝1或＋＝1，‎ 即x＋2y－2＝0或2x＋y＋2＝0为所求直线的方程．‎ 答案：x＋2y－2＝0或2x＋y＋2＝0‎ ‎9．已知直线l：＋＝1.‎ ‎(1)若直线l的斜率等于2，求实数m的值；‎ ‎(2)若直线l分别与x轴、y轴的正半轴交于A，B两点，O是坐标原点，求△AOB面积的最大值及此时直线的方程．‎ 解：(1)根据直线l的方程：＋＝1可得直线l过点(m，0)，(0，4－m)，所以k＝＝2，解得m＝－4.‎ ‎(2)直线l过点(m，0)，(0，4－m)，则由m>0，4－m>0得0