山西大学附中2019届高三下学期3月模块诊断 文科数学 17页

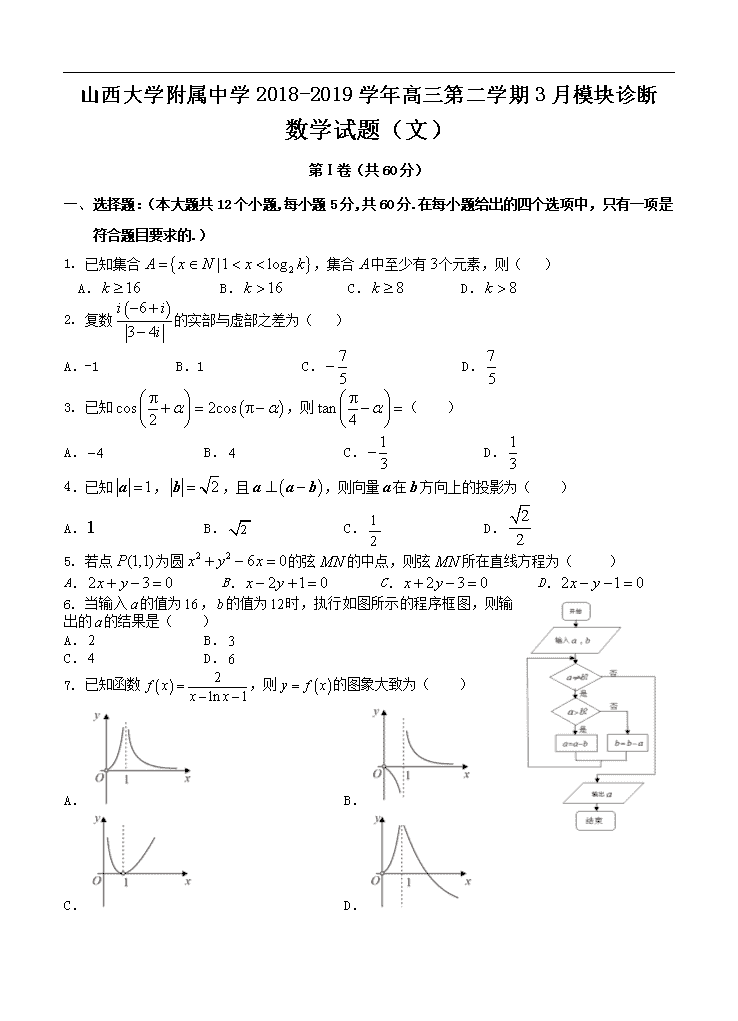
山西大学附属中学2018-2019学年高三第二学期3月模块诊断 数学试题（文）‎ 第Ⅰ卷（共60分）‎ 一、 选择题：（本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1. 已知集合，集合中至少有个元素，则（ ）‎ A． B． C． D．‎ ‎2. 复数的实部与虚部之差为（ ）‎ A．-1 B．1 C． D．‎ ‎3. 已知，则（ ）‎ A． B． C． D．‎ ‎4．已知，，且，则向量在方向上的投影为（ ）‎ A． B． C． D．‎ ‎5. 若点为圆的弦的中点，则弦所在直线方程为（ ）‎ A． ‎ B． ‎ C． ‎ D． ‎ ‎6. 当输入的值为，的值为时，执行如图所示的程序框图，则输出的的结果是（ ）‎ A． B． ‎ C． D．‎ ‎7. 已知函数，则的图象大致为（ ）‎ A． B．‎ C． D．‎ ‎8．如图，在棱长为的正方体中，为的中点，为上任意一点， 、为上两点，且的长为定值，则下面四个值中不是定值的是（ ）‎ A．点到平面的距离 ‎ B．直线与平面所成的角 C．三棱锥的体积 ‎ D．△的面积 ‎9．将函数的图象向右平移个单位长度得到图像，则下列判断错误的是（ ）‎ A．函数在区间上单调递增 B．图像关于直线对称 C．函数在区间上单调递减 D．图像关于点对称 ‎10. 设锐角的三个内角，，的对边分别为，，，且，，则周长的取值范围为（ ）‎ A． B． ‎ C． D．‎ ‎11. 设双曲线的左、右焦点分别为，，过的直线分别交双曲线左右两支于点，，连结，，若，，则双曲线的离心率为（ ）‎ A． B． C． D．‎ ‎12.已知函数（为自然对数的底），若方程有且仅有两个不同的解，则实数的取值范围是（ ） ‎ A. B. C. D. ‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13. 已知点在不等式组表示的平面区域上运动，则的取值范围是 ‎ ‎14．已知点及抛物线上一动点则的最小值是　　　‎ ‎15. 已知数列为正项的递增等比数列，，，记数列的前项和为，则使不等式成立的正整数的最大值为_______．‎ ‎16. 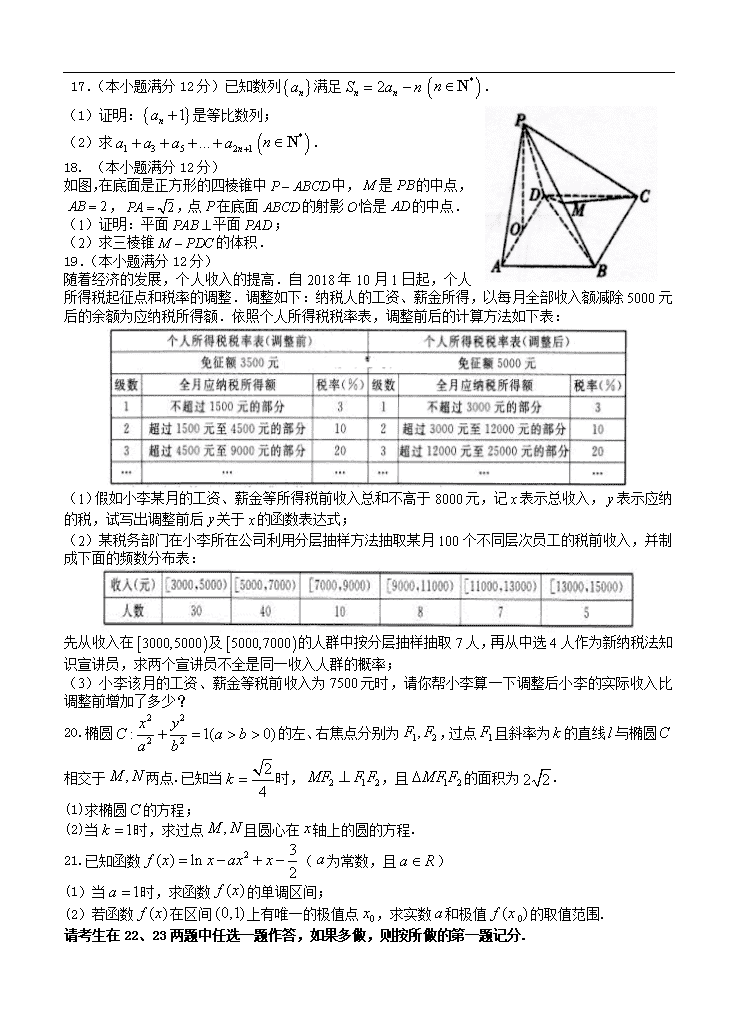已知在四面体中，，则该四面体的体积的最大值为___________． ‎ 三、解答题（解答应写出文字说明、证明过程或演算步骤.）‎ ‎ 17．（本小题满分12分）已知数列满足．‎ ‎（1）证明：是等比数列；‎ ‎（2）求．‎ ‎18. （本小题满分12分）‎ 如图，在底面是正方形的四棱锥中中，是的中点，，，点在底面的射影恰是的中点．‎ ‎（1）证明：平面平面；‎ ‎（2）求三棱锥的体积．‎ ‎19．（本小题满分12分）‎ 随着经济的发展，个人收入的提高．自2018年10月1日起，个人所得税起征点和税率的调整．调整如下：纳税人的工资、薪金所得，以每月全部收入额减除5000元后的余额为应纳税所得额．依照个人所得税税率表，调整前后的计算方法如下表：‎ ‎（1）假如小李某月的工资、薪金等所得税前收入总和不高于8000元，记表示总收入，表示应纳的税，试写出调整前后关于的函数表达式；‎ ‎（2）某税务部门在小李所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入，并制成下面的频数分布表：‎ 先从收入在及的人群中按分层抽样抽取7人，再从中选4人作为新纳税法知识宣讲员，求两个宣讲员不全是同一收入人群的概率；‎ ‎（3）小李该月的工资、薪金等税前收入为7500元时，请你帮小李算一下调整后小李的实际收入比调整前增加了多少？‎ ‎20.椭圆的左、右焦点分别为，过点且斜率为的直线与椭圆相交于两点.已知当时，，且的面积为.‎ ‎(1)求椭圆的方程；‎ ‎(2)当时，求过点且圆心在轴上的圆的方程.‎ ‎21.已知函数（为常数，且）‎ ‎(1）当时，求函数的单调区间；‎ ‎(2）若函数在区间上有唯一的极值点，求实数和极值的取值范围.‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22. （10分）选修4-4：坐标系与参数方程 在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．为曲线上的动点，点在射线上，且满足．‎ ‎（Ⅰ）求点的轨迹的直角坐标方程；‎ ‎（Ⅱ）设与轴交于点，过点且倾斜角为的直线与相交于两点，求的值．‎ ‎23．选修4-5：不等式选讲 已知函数．‎ ‎（1）当时，解不等式；‎ ‎（2）设不等式的解集为，若，求实数的取值范围．‎ 数学（理）参考答案 第Ⅰ卷（共60分）‎ 一、 选择题：（本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，‎ 只有一项是符合题目要求的.）‎ ‎1. 已知集合，集合中至少有个元素，则（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ 试题分析：由集合中至少有个元素，则，解得，故选B.学科网 ‎2. 复数的实部与虚部之差为（ ）‎ A．-1 B．1 C． D．‎ ‎【答案】B ‎3. 已知，则（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】因为，所以，‎ 所以，故选C．‎ ‎4．已知，，且，则向量在方向上的投影为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】设与的夹角为，，，，，∴向量在方向上的投影为，‎ 故选D．‎ ‎6. 当输入的值为，的值为时，执行如图所示的程序框图，则输出的的结果是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】模拟程序的运行，可得，，‎ 满足条件，满足条件，，‎ 满足条件，不满足条件，，‎ 满足条件，不满足条件，，‎ 不满足条件，输出的值为4．故选C．‎ ‎7. 已知函数，则的图象大致为（ ）‎ A． B．‎ C． D．‎ ‎7．【答案】A ‎【解析】由于，排除B选项．‎ 由于，，，函数单调递减，排除C选项．‎ 由于，排除D选项．故选A．‎ ‎8．如图，在棱长为的正方体中，为的中点，为上任意一点， 、为上两点，且的长为定值，则下面四个值中不是定值的是（ ）‎ A．点到平面的距离 ‎ B．直线与平面所成的角 C．三棱锥的体积 ‎ D．△的面积 ‎8.【答案】B ‎【解析】‎ 试题分析：将平面延展到平面如下图所示，由图可知，到平面的距离为定值.由于四边形为矩形，故三角形的面积为定值，进而三棱锥的体积为定值.故A，C，D选项为真命题，B为假命题.‎ ‎9．将函数的图象向右平移个单位长度得到图像，则下列判断错误的是（ ）‎ A．函数在区间上单调递增 B．图像关于直线对称 C．函数在区间上单调递减 D．图像关于点对称 ‎9．【答案】C ‎【解析】由题意，将函数的图象向右平移个单位长度，‎ 可得，‎ 对于A中，由，则，‎ 则函数在区间上单调递增是正确的；‎ 对于B中，令，则，‎ ‎∴函数图像关于直线对称是正确的；‎ 对于C中，，则，‎ 则函数在区间上先减后增，∴不正确；‎ 对于D中，令，则，‎ ‎∴图像关于点对称是正确的，故选C．‎ ‎10. 设锐角的三个内角，，的对边分别为，，，且，，则周长的取值范围为（ ）‎ A． B． ‎ C． D．‎ ‎【答案】C ‎【解析】因为为锐角三角形，所以，，，即，，，所以，；又因为，‎ 所以，又因为，所以；由，‎ 即，所以，令，‎ 则，又因为函数在上单调递增，所以函数值域为，故选：C．‎ ‎11. 设双曲线的左、右焦点分别为，，过的直线分别交双曲线左右两支于点，，连结，，若，，则双曲线的离心率为（ ）‎ A． B． C． D．‎ ‎11．【答案】B ‎【解析】结合题意可知，设，则，，‎ 则结合双曲线的性质可得，，，‎ 代入，解得，∴，，，‎ 对三角形运用余弦定理，得到 ‎，‎ 解得．故选B．‎ ‎12.已知函数（为自然对数的底），若方程有且仅有两个不同的解，则实数的取值范围是（ ） ‎ A. B. C. D. ‎ ‎，，所以方程可以化为：‎ ‎，即，记，，设直与图像相切时的切点为，则切线方程为，过点，所以或（舍），所以切线的斜率为，由图像可以得．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13. 已知点在不等式组表示的平面区域上运动，则的取值范围是 ‎ ‎13．【答案】‎ 试题分析：由题意得，画出不等式组所表示的平面区域，如图所示，平移直线过点时，有最小值为；平移直线过点时，有最大值为，所以的取值范围是，‎ ‎14．已知点及抛物线上一动点则的最小值是　　　‎ ‎14．【答案】2‎ ‎15. 已知数列为正项的递增等比数列，，，记数列的前项和为，则使不等式成立的正整数的最大值为_______．‎ ‎15．【答案】6‎ ‎【解析】数列为正项的递增等比数列，，，‎ 即，解得，则公比，∴，‎ 则，∴，‎ 即，得，此时正整数的最大值为6．故答案为6．‎ ‎16（理）. 已知在四面体中，，则该四面体的体积的最大值为___________． ‎ ‎16．答案：‎ 解析：取中点，连接，要使得四面体的体积最大，‎ 则必有平面平面，设，‎ 则，‎ 则，‎ 则，令，得，当时，取得最大值．‎ 三、解答题（解答应写出文字说明、证明过程或演算步骤.）‎ ‎ (文)17．（本小题满分12分）已知数列满足．‎ ‎（1）证明：是等比数列；‎ ‎（2）求．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【解析】（1）由得：，···········1分 因为，‎ 所以，···········3分 从而由得，···········5分 所以是以为首项，为公比的等比数列．···········6分 ‎（2）由（1）得，···········8分 所以 ‎．···········12分 ‎（文科）18. （本小题满分12分）‎ 如图，在底面是正方形的四棱锥中中，是的中点，，，点在底面的射影恰是的中点．‎ ‎（1）证明：平面平面；‎ ‎（2）求三棱锥的体积．‎ ‎【解析】（1）证明：依题意，得平面，‎ 又平面，∴．‎ 又，，∴平面．‎ 又平面，‎ ‎∴平面平面．‎ ‎（2）∵平面，为的中点，∴为等腰三角形，‎ 又，，∴，，．‎ ‎∵点是的中点，∴到平面的距离等于点到平面距离的一半，‎ ‎，‎ 即三棱锥的体积为．‎ ‎19．（12分）[2019·衡水金卷]随着经济的发展，个人收入的提高．自2018年10月1日起，个人所得税起征点和税率的调整．调整如下：纳税人的工资、薪金所得，以每月全部收入额减除5000元后的余额为应纳税所得额．依照个人所得税税率表，调整前后的计算方法如下表：‎ ‎（1）假如小李某月的工资、薪金等所得税前收入总和不高于8000元，记表示总收入，表示应纳的税，试写出调整前后关于的函数表达式；‎ ‎（2）某税务部门在小李所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入，并制成下面的频数分布表：‎ 先从收入在及的人群中按分层抽样抽取7人，再从中选4人作为新纳税法知识宣讲员，求两个宣讲员不全是同一收入人群的概率；‎ ‎（3）小李该月的工资、薪金等税前收入为7500元时，请你帮小李算一下调整后小李的实际收入比调整前增加了多少？‎ ‎【答案】（1）见解析；（2）；（3）见解析．‎ ‎【解析】（1）调整前关于的表达式为．‎ 调整后关于的表达式为，‎ ‎（2）由频数分布表可知从及的人群中按分层抽样抽取7人，‎ 其中中占3人，分别记为A，B，C，中占4人，‎ 分别记为1，2，3，4，再从这7人中选2人的所有组合有：AB，AC，A1，A2，A3，A4，BC，B1，B2，B3，B4，C1，C2，C3，C4，12，13，14，23，24，34，共21种情况，‎ 其中不在同一收入人群的有：Al，A2，A3，A4，B1，B2，B3，B4，C1，C2，C3，C4，‎ 共12种，∴所求概率为．‎ ‎（3）由于小李的工资、薪金等收入为7500元，‎ 按调整前起征点应纳个税为元；‎ 按调整后起征点应纳个税为元，‎ 比较两个纳税方案可知，按调整后起征点应纳个税少交220元，‎ 即个人的实际收入增加了220元，∴小李的实际收入增加了220元．‎ ‎（文科）20.椭圆的左、右焦点分别为，过点且斜率为的直线与椭圆相交于两点.已知当时，，且的面积为.‎ ‎(1)求椭圆的方程；‎ ‎(2)当时，求过点且圆心在轴上的圆的方程.‎ 答案：‎ ‎(1)‎ ‎(2)‎ 解答：‎ 本题考查了椭圆的标准方程与几何性质、直线方程，考查了数形结合思想、特殊与一般思想，突显了直观想象、数学运算、逻辑推理的考查。解答本题第一问首先要根据题设给的点 的特殊位置，建立关于的等式，再通过解方程求出，从而得到所求标准方程；解答本题第二问首先要根据三角形外接圆圆心的定义，计算出线段的中垂线与轴的交点坐标，从而确定圆心，然后再由圆心与点的距离算得圆的半径，最后得到圆的标准方程. 关键是如何得到圆心的坐标和半径的大小.‎ ‎(1)由已知得：当时，，‎ 此时， ………………2分 ‎ 所以，， ………………4分 ‎ 所以椭圆的方程为. ………………5分 ‎ ‎(2)当时，，‎ 代入椭圆的方程得：，所以，， ………………6分 ‎ 所以，线段的中点坐标， ………………7分 ‎ 线段的中垂线方程为，令， ………………9分 即圆心坐标为，所以半径， ………………11分 因此所求圆的方程为：. ………………12分 ‎（文科）21.已知函数（为常数，且）‎ ‎(1）当时，求函数的单调区间；‎ ‎(2）若函数在区间上有唯一的极值点，求实数和极值的取值范围.‎ 答案：‎ ‎(1) 函数的递增区间是，递减区间是；‎ ‎(2) ‎ 解答：‎ 本题考查了导数的计算、导数的应用，考查了函数与方程思想、数形结合思想，突显了数学建模的考查。解答本题第一问首先要确定函数定义域并求导，然后根据导数的正负结合解不等式确定单调区间。解答本题第二问首先要根据的分子构造二次函数 ‎，借助二次函数图像结合条件确定实数的范围，然后利用隐含条件消元，消掉，建立极值与的函数关系式，确定函数模型，然后根据新函数的单调性确定范围. 本题第二问难点是有两个变量，需要根据隐含条件合理消元.‎ ‎(1)（， ………………1分 当时， ………………2分 由解得， ………………3分 ‎ 所以函数的递增区间是，递减区间是； ………………5分 ‎ ‎(2)记，，函数在区间上有唯一极值点，‎ 则函数图像是开口向下的抛物线，且，即，‎ 所以的取值范围是， ………………7分 ‎ ‎，‎ 所以，………9分 ‎ 因为在上单调递增，且时，，，‎ 所以的取值范围是. ………………12分 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22. （10分）选修4-4：坐标系与参数方程 在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．为曲线上的动点，点在射线上，且满足．‎ ‎（Ⅰ）求点的轨迹的直角坐标方程；‎ ‎（Ⅱ）设与轴交于点，过点且倾斜角为的直线与相交于两点，求的值．‎ 答案：‎ ‎（Ⅰ）；‎ ‎（Ⅱ）.‎ 解答：‎ ‎【评析】本题考查直线与圆的极坐标方程、极坐标方程与直角坐标方程的互化、直线参数方程的应用，突显了直观想象的考查.解答本题第一问首先要依据动点的极坐标的关系找到点的极坐标方程，再化为直角坐标方程；解答本题第二问首先要根据条件确定直线的参数方程，依据参数的几何意义，结合解方程，利用韦达定理得到解.‎ ‎（Ⅰ）设的极坐标为，的极坐标为，‎ 由题设知．所以， ………………2分 ‎ 即的极坐标方程，所以的直角坐标方程为． ………………5分 ‎（Ⅱ）交点，所以直线的参数方程为（为参数），‎ 曲线的直角坐标方程，‎ 代入得：，， ………………8分 ‎ 设方程两根为，则分别是对应的参数，‎ 所以． ………………10分 ‎23．选修4-5：不等式选讲 已知函数．‎ ‎（1）当时，解不等式；‎ ‎（2）设不等式的解集为，若，求实数的取值范围．‎ ‎【答案】（1）；（2）．‎ ‎【解析】（1）当时，原不等式可化为．‎ ‎①当时，原不等式可化为，解得，所以；‎ ‎②当时，原不等式可化为，解得，所以；‎ ‎③当时，原不等式可化为，解得，所以．‎ 综上所述，当时，不等式的解集为．·····5分 ‎（2）不等式可化为，‎ 依题意不等式在恒成立，‎ 所以，即，即，‎ 所以．解得，‎ 故所求实数的取值范围是．·····10分 欢迎访问“高中试卷网”——http://sj.fjjy.org