【数学】2020届一轮复习北师大版第6讲离散型随机变量的均值与方差学案 12页

第6讲　离散型随机变量的均值与方差 ‎[最新考纲]‎ ‎1．理解取有限个值的离散型随机变量的均值、方差的概念．‎ ‎2．能计算简单离散型随机变量的均值、方差，并能解决一些简单实际问题.‎ 知 识 梳 理 ‎1．离散型随机变量的均值与方差 若离散型随机变量X的分布列为P(X＝xi)＝pi，i＝1,2，…，n ‎(1)均值：称E(X)＝x1p1＋x2p2＋…＋xipi＋…＋xnpn为随机变量X的均值或数学期望．‎ ‎(2)方差：称D(X)＝(xi－E(X))2pi为随机变量X的方差，其算术平方根为随机变量X的标准差．‎ ‎2．均值与方差的性质 ‎(1)E(aX＋b)＝aE(X)＋b.‎ ‎(2)D(aX＋b)＝a2D(X)．(a，b为常数)‎ ‎3．两点分布与二项分布的均值、方差 均值 方差 变量X服从两点分布 E(X)＝p D(X)＝p(1－p)‎ X～B(n，p)‎ E(X)＝np D(X)＝np(1－p)‎ 辨 析 感 悟 ‎1．离散型随机变量的均值与方差 ‎(1)期望是算术平均数概念的推广，与概率无关．(×)‎ ‎(2)(教材习题改编)在篮球比赛中，罚球命中1次得1分，不中得0分．如果某运动员罚球命中的概率为0.7，那么他罚球1次的得分X的均值是0.7，方差是0.21.(√)‎ ‎2．均值与方差的性质 ‎(3)随机变量的方差和标准差都反映了随机变量取值偏离均值的平均程度，方差或标准差越小，则偏离均值的平均程度越小．(√)‎ ‎(4)已知X的分布列为 X ‎－1‎ ‎0‎ ‎1‎ P 设Y＝2X＋3，则E(Y)的值为.(√)‎ ‎(5)(2018·上海卷改编)设等差数列x1，x2，x3，…，x19的公差为1，若随机变量X等可能地取值x1，x2，x3，…，x19，则方差D(X)＝30.(√)‎ ‎[感悟·提升]‎ ‎1．对均值(或数学期望)的理解 ‎(1)期望是算术平均值概念的推广，是概率意义下的平均，如(1)．‎ ‎(2)E(X)是一个实数，由X的分布列唯一确定，即X作为随机变量是可变的，而E(X)是不变的，它描述X取值的平均状态．‎ ‎(3)公式E(X)＝x1p1＋x2p2＋…＋xnpn直接给出了E(X)的求法，即随机变量取值与相应概率值分别相乘后相加，由此可知，求E(X)的关键在于写出随机变量的分布列．‎ ‎2．方差的意义 D(X)表示随机变量X对E(X)的平均偏离程度，D(X)越大表明平均偏离程度越大，说明X的取值越分散，反之，D(X)越小，X的取值越集中．在E(X)附近，统计中常用来描述X的分散程度，如(5).‎ 考点一　离散型随机变量的均值与方差 ‎【例1】 (2018·浙江卷)设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分．‎ ‎(1)当a＝3，b＝2，c＝1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量X为取出此2球所得分数之和，求X的分布列；‎ ‎(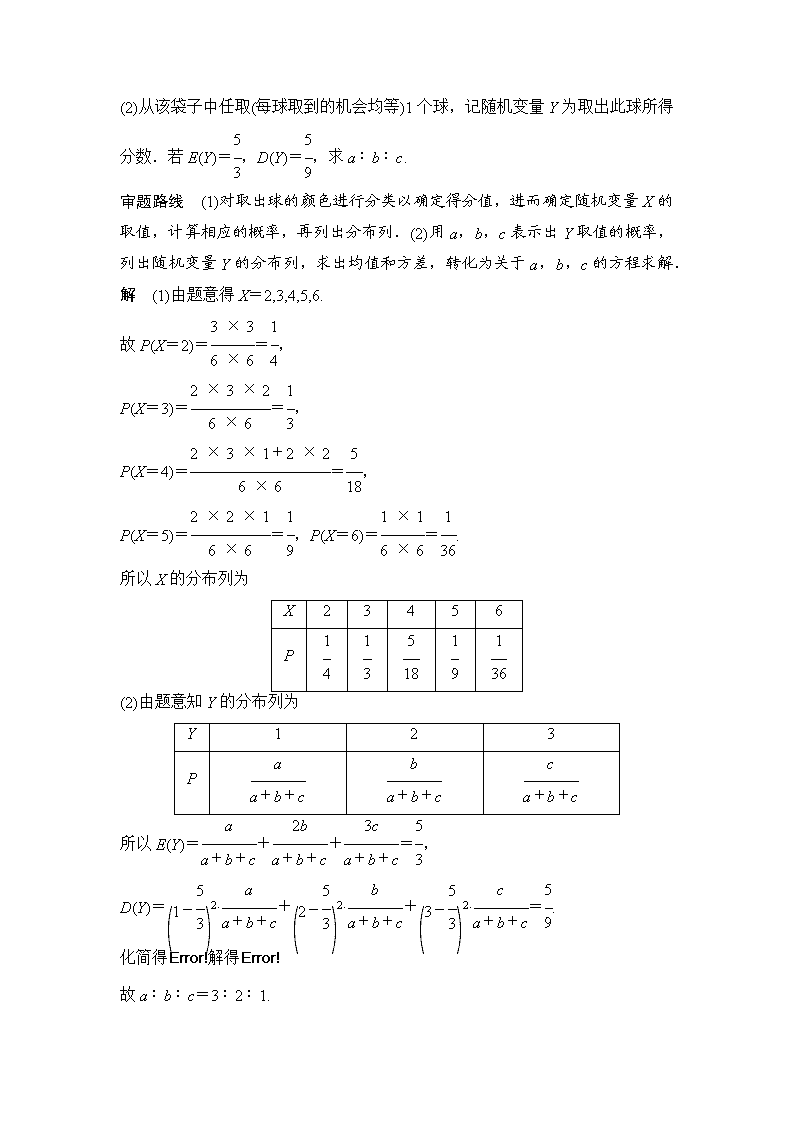2)从该袋子中任取(每球取到的机会均等)1个球，记随机变量Y为取出此球所得 分数．若E(Y)＝，D(Y)＝，求a∶b∶c.‎ 审题路线　(1)对取出球的颜色进行分类以确定得分值，进而确定随机变量X的取值，计算相应的概率，再列出分布列．(2)用a，b，c表示出Y取值的概率，列出随机变量Y的分布列，求出均值和方差，转化为关于a，b，c的方程求解．‎ 解　(1)由题意得X＝2,3,4,5,6.‎ 故P(X＝2)＝＝，‎ P(X＝3)＝＝，‎ P(X＝4)＝＝，‎ P(X＝5)＝＝，P(X＝6)＝＝.‎ 所以X的分布列为 X ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ P ‎(2)由题意知Y的分布列为 Y ‎1‎ ‎2‎ ‎3‎ P 所以E(Y)＝＋＋＝，‎ D(Y)＝2·＋2·＋2·＝.‎ 化简得解得 故a∶b∶c＝3∶2∶1.‎ 学生用书第196页 规律方法 求解该类问题，首先要理解问题的关键，其次要准确无误地找出随机变量的所有可能取值，计算出相应的概率，写出随机变量的分布列，正确运用均值、方差公式进行计算，也就是要过“三关”：①阅读理解关；②概率计算关；③‎ 公式应用关，如方差、均值公式要准确理解、记忆．‎ ‎【训练1】 (2018·南昌质检)如图，从A1(1,0,0)，A2(2,0,0)，B1(0,1,0)，B2(0,2,0)，C1(0,0,1)，‎ C2(0,0,2)这6个点中随机选取3个点，将这3个点及原点O两两相连构成一个“立体”，‎ 记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内，此时“立体”的体积V＝0)．‎ ‎(1)求V＝0的概率；‎ ‎(2)求V的分布列及数学期望E(V)．‎ 解　(1)从6个点中随机选取3个点总共有C＝20(种)取法，选取的3个点与原点在同一个平面内的取法有CC＝12(种)，因此V＝0的概率为P(V＝0)＝＝.‎ ‎(2)V的所有可能取值为0，，，，，‎ 又P(V＝)＝，‎ P(V＝)＝＝，‎ P(V＝)＝＝，‎ P(V＝)＝，‎ 因此V的分布列为 V ‎0‎ P 由V的分布列可得 E(V)＝0×＋×＋×＋×＋× ‎＝.‎ 考点二　与二项分布有关的均值、方差 ‎【例2】 (2018·福建卷)某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为，中奖可以获得2分；方案乙的中奖率为，中奖可以获得3分；未中奖则不得分．每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品．‎ ‎(1)若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X，求X≤3的概率；‎ ‎(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖，问：他们选择何种方案抽奖，累计得分的数学期望较大？‎ 审题路线　(1)易知X＝0,2,3,5，则“X≤3”与“X＝5”为对立事件，根据相互独立事件与对立事件公式计算．(2)每种方案的得分与中奖次数有关，且中奖次数服从二项分布，运用均值的性质求解．‎ 解　(1)由已知得，小明中奖的概率为，小红中奖的概率为，且两人中奖与否互不影响．‎ 记“这2人的累计得分X≤‎3”‎的事件为A，‎ 则事件A的对立事件为“X＝5”，‎ 因为P(X＝5)＝×＝，‎ 所以P(A)＝1－P(X＝5)＝，‎ 即这2人的累计得分X≤3的概率为.‎ ‎(2)法一　设小明、小红都选择方案甲抽奖中奖次数为X1，都选择方案乙抽奖中奖次数为X2，则这两人选择方案甲抽奖累计得分的数学期望为E(2X1)，选择方案乙抽奖累计得分的数学期望为E(3X2)．‎ 由已知可得，X1～B，X2～B，‎ 所以E(X1)＝2×＝，E(X2)＝2×＝，‎ 因此E(2X1)＝2E(X1)＝，E(3X2)＝3E(X2)＝.‎ 因为E(2X1)>E(3X2)，‎ 所以他们都选择方案甲进行抽奖时，累计得分的数学期望较大．‎ 法二　设小明、小红都选择方案甲所获得的累计得分为Y1，都选择方案乙所获得的累计得分为Y2，则Y1，Y2的分布列为：‎ Y1‎ ‎0‎ ‎2‎ ‎4‎ P ‎　‎ Y2‎ ‎0‎ ‎3‎ ‎6‎ P ‎∴E(Y1)＝0×＋2×＋4×＝，‎ E(Y2)＝0×＋3×＋6×＝，‎ 因为E(Y1)>E(Y2)，‎ 所以二人都选择方案甲抽奖，累计得分的数学期望较大．‎ 规律方法 求离散型随机变量的均值与方差的方法：(1)先求随机变量的分布列，然后利用均值与方差的定义求解．(2)若随机变量X～B(n，p)，则可直接使用公式E(X)＝np，D(X)＝np(1－p)求解．‎ ‎【训练2】 某人投弹命中目标的概率p＝0.8.‎ ‎(1)求投弹一次，命中次数X的均值和方差；‎ ‎(2)求重复10次投弹时命中次数Y的均值和方差．‎ 解　(1)随机变量X的分布列为 X ‎0‎ ‎1‎ P ‎0.2‎ ‎0.8‎ 因为X服从两点分布，故E(X)＝p＝0.8，D(X)＝p(1－p)＝0.8×0.2＝0.16.‎ ‎(2)由题意知，命中次数Y服从二项分布，‎ 即Y～B(10,0.8)，‎ ‎∴E(Y)＝np＝10×0.8＝8，D(Y)＝np(1－p)＝10×0.8×0.2＝1.6.‎ 学生用书第197页 考点三　均值与方差在决策中的应用 ‎【例3】 某投资公司在2018年年初准备将1 000万元投资到“低碳”项目上，现有两个项目供选择：‎ 项目一：新能源汽车．据市场调研，投资到该项目上，到年底可能获利30%，也可能亏损15%，且这两种情况发生的概率分别为和；‎ 项目二：通信设备．据市场调研，投资到该项目上，到年底可能获利50%，可能损失30%，也可能不赔不赚，且这三种情况发生的概率分别为，和.‎ ‎(1)针对以上两个投资项目，请你为投资公司选择一个合理的项目，并说明理由；‎ ‎(2)若市场预期不变，该投资公司按照你选择的项目长期投资(每一年的利润和本金继续用作投资)，问大约在哪一年的年底总资产(利润＋本金)可以翻一番？‎ ‎(参考数据：lg 2≈0.301 0，lg 3≈0.477 1)‎ 解　(1)若按“项目一”投资，设获利为X1万元．则X1的分布列为 X1‎ ‎300‎ ‎－150‎ P ‎∴E(X1)＝300×＋(－150)×＝200(万元)．‎ 若按“项目二”投资，设获利X2万元，‎ 则X2的分布列为：‎ X2‎ ‎500‎ ‎－300‎ ‎0‎ P ‎∴E(X2)＝500×＋(－300)×＋0×＝200(万元)．‎ D(X1)＝(300－200)2×＋(－150－200)2×＝35 000，‎ D(X2)＝(500－200)2×＋(－300－200)2×＋(0－200)2×＝140 000.‎ 所以E(X1)＝E(X2)，D(X1)2‎ ‎02‎ 轿车数量(辆)‎ ‎2‎ ‎3‎ ‎45‎ ‎5‎ ‎45‎ 每辆利润 ‎(万元)‎ ‎1‎ ‎2‎ ‎3‎ ‎1.8‎ ‎2.9‎ 将频率视为概率，解答下列问题：‎ ‎(1)从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率．‎ ‎(2)若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为X1，生产一辆乙品牌轿车的利润为X2，分别求X1，X2的分布列．‎ ‎(3)该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车．若从经济效益的角度考虑，你认为应生产哪种品牌的轿车？说明理由．‎ 解　(1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A，则P(A)＝＝.‎ ‎(2)依题意得，X1的分布列为 X1‎ ‎1‎ ‎2‎ ‎3‎ P X2的分布列为 X2‎ ‎1.8‎ ‎2.9‎ P ‎(3)由(2)得E(X1)＝1×＋2×＋3×＝＝‎ ‎2．86(万元)，‎ E(X2)＝1.8×＋2.9×＝2.79(万元)．‎ 因为E(X1)>E(X2)，所以应生产甲品牌轿车．‎ ‎1．均值与方差的性质 ‎(1)E(aX＋b)＝aE(X)＋b，D(aX＋b)＝a2D(X)(a，b为常数)．‎ ‎(2)若X服从两点分布，则E(X)＝p，D(X)＝p(1－p)．‎ ‎(3)若X服从二项分布，即X～B(n，p)，则E(X)＝np，D(X)＝np(1－p)．‎ ‎2．求离散型随机变量均值与方差的基本方法 ‎(1)已知随机变量的分布列求它的均值、方差，按定义求解．‎ ‎(2)已知随机变量X的均值、方差，求X的线性函数Y＝aX＋b的均值、方差，可直接用X的均值、方差的性质求解．‎ ‎(3)如果所给随机变量是服从常用的分布(如两点分布、二项分布等)，利用它们的均值、方差公式求解．‎ ‎　　　　　　　　　　　　　　　　　　‎ 学生用书第198页 易错辨析12——不能正确理解题目条件致误 ‎【典例】 (2018·石家庄调研)根据以往的经验，某工程施工期间的降水量X(单位：mm)对工期的影响如下表：‎ 降水量X X<300‎ ‎300≤X<700‎ ‎700≤X<900‎ X≥900‎ 工期延误天数Y ‎0‎ ‎2‎ ‎6‎ ‎10‎ 历年气象资料表明，该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9，求：‎ ‎(1)工程延误天数Y的均值与方差；‎ ‎(2)在降水量X至少是300的条件下，工期延误不超过6天的概率．‎ ‎[错解]　(1)由条件和概率的加法有：P(X<300)＝0.3，‎ P(300≤X＜700)＝P(X<700)－P(X<300)＝0.7－0.3＝0.4，‎ P(700≤X＜900)＝P(X<900)－P(X<700)＝0.9－0.7＝0.2，‎ P(X≥900)＝1－P(X<900)＝1－0.9＝0.1.‎ 所以Y的分布列为：‎ Y ‎0‎ ‎2‎ ‎6‎ ‎10‎ P ‎0.3‎ ‎0.4‎ ‎0.2‎ ‎0.1‎ 于是，E(Y)＝0×0.3＋2×0.4＋6×0.2＋10×0.1＝3；‎ D(Y)＝(0－3)2×0.3＋(2－3)2×0.4＋(6－3)2×0.2＋(10－3)2×0.1＝9.8.‎ 故工期延误天数Y的均值为3，方差为9.8.‎ ‎(2)由(1)知，在降水量X至少是‎300 mm条件下，工期不超过6天的概率为P＝P(Y＝2)＋P(Y＝6)＝0.4＋0.2＝0.6.‎ ‎[错因]　第(2)问中，在降水量X至少是‎300 mm的条件下，这一条件说明是在延误工期的条件下，求工期延误不超过6天的概率，错解中没有在这条件下求概率．‎ ‎[正解]　(1)同上述解法．‎ ‎(2)由概率加法， 得P(X≥300)＝1－P(X<300)＝0.7，‎ 又P(300≤X<900)＝P(X<900)－P(X<300)＝0.9－0.3＝0.6.‎ 由条件概率，得P(Y≤6|X≥300)＝P(X<900|X≥300)＝＝＝.‎ 故在降水量X至少是‎300 mm的条件下，工期延误不超过6天的概率是.‎ ‎[防范措施]　(1)求某事件概率，首先理解题意，分清概率模型，恰当选择概率计算公式，本题是条件概率，应利用条件概率公式计算．‎ ‎(2)解决均值和方差问题时，认真计算，正确利用均值和方差公式，避免失误．‎ ‎【自主体验】‎ ‎　(2018·北京卷)下图是某市‎3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染．某人随机选择‎3月1日至3月13日中的某一天到达该市，并停留2天．‎ ‎(1)求此人到达当日空气重度污染的概率；‎ ‎(2)设X是此人停留期间空气质量优良的天数，求X的分布列与数学期望；‎ ‎(3)由图判断从哪天开始连续三天的空气质量指数方差最大？(结论不要求证明)‎ 解　设Ai表示事件“此人于3月i日到达该市”(i＝1,2，…，13)．‎ 根据题意，P(Ai)＝，且Ai∩Aj＝∅(i≠j)．‎ ‎(1)设B为事件“此人到达当日空气重度污染”，则B＝A5∪A8.‎ 所以P(B)＝P(A5∪A8)＝P(A5)＋P(A8)＝.‎ ‎(2)由题意可知，X的所有可能取值为0,1,2，且P(X＝1)＝P(A3∪A6∪A7∪A11)‎ ‎＝P(A3)＋P(A6)＋P(A7)＋P(A11)＝.‎ P(X＝2)＝P(A1∪A2∪A12∪A13)‎ ‎＝P(A1)＋P(A2)＋P(A12)＋P(A13)＝.‎ P(X＝0)＝1－P(X＝1)－P(X＝2)＝.‎ 所以X的分布列为 X ‎0‎ ‎1‎ ‎2‎ P 故X的数学期望E(X)＝0×＋1×＋2×＝.‎ ‎(3)从‎3月5日开始连续三天的空气质量指数方差最大．‎ 好的先生不是教书，不是教学生，乃是教学生学。——陶行知 活的人才教育不是灌输知识，而是将开发文化宝库的钥匙，尽我们知道的交给学生。——陶行知 教育不能创造什么，但它能启发儿童创造力以从事于创造工作。——陶行知 我们发现了儿童有创造力，认识了儿童有创造力，就须进一步把儿童的创造力解放出来。——陶行知