【数学】2018届一轮复习北师大版空间向量在立体几何中的应用（理）教案 15页

第七节　空间向量在立体几何中的应用 ‎[考纲传真]　1.理解直线的方向向量与平面的法向量.2.能用向量语言表述直线与直线、直线与平面、平面与平面的平行、垂直关系.3.能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理).4.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题，了解向量方法在研究立体几何问题中的应用．‎ ‎1．直线的方向向量和平面的法向量 ‎(1)直线的方向向量 l是空间一直线，A，B是直线l上任意两点，则称为直线l的方向向量．(与平行的任意非零向量a也是直线l的方向向量)‎ ‎(2)平面的法向量 如果直线l垂直于平面α，那么把直线l的方向向量a叫作平面α的法向量．(所有与直线l平行的非零向量都是平面α的法向量) ‎ ‎2．夹角的计算 ‎(1)直线间的夹角 设s1，s2分别是两异面直线l1，l2的方向向量，则 l1与l2的夹角θ s1与s2的夹角〈s1，s2〉‎ 范围 ‎(0，π)‎ 求法 cos θ＝|cos〈s1，s2〉＝|‎ cos〈s1，s2〉＝ 关系 当0<〈s1，s2〉≤时，θ＝〈s1，s2〉；当<〈s1，s2〉<π时，θ＝π－〈s1，s2〉‎ ‎(2)平面间的夹角 已知平面π1和π2的法向量分别为n1和n2，‎ 当0≤〈n1，n2〉≤时，平面π1与π2的夹角等于〈n1，n2〉；‎ 当<〈n1，n2〉≤π时，平面π1与π2的夹角等于π－〈n1，n2〉．‎ ‎(3)直线与平面的夹角 设直线l的方向向量为s，平面π的法向量为n，直线l与平面π的夹角为θ，则sin θ＝|cos〈s，n〉|＝.‎ ‎1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)两直线的方向向量所成的角就是两条直线所成的角．(　　)‎ ‎(2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角．(　　)‎ ‎(3)两个平面的法向量所成的角是这两个平面所成的角．(　　)‎ ‎(4)两异面直线夹角的范围是，直线与平面所成角的范围是，二面角的范围是[0，π]．(　　)‎ ‎[答案]　(1)×　(2)×　(3)×　(4)√‎ ‎2．(教材改编)设u＝(－2,2，t)，v＝(6，－4,4)分别是平面α，β的法向量．若α⊥β，则t＝(　　)‎ A．3　　　　　B．4　　　　C．5　　　　D．6‎ C　[∵α⊥β，则u·v＝－2×6＋2×(－4)＋4t＝0，‎ ‎∴t＝5.]‎ ‎3．(2014·全国卷Ⅱ)直三棱柱ABCA1B1C1中，∠BCA＝90°，M，N分别是A1B1，A1C1的中点，BC＝CA＝CC1，则BM与AN所成角的余弦值为(　　)‎ A. B． ‎ C. 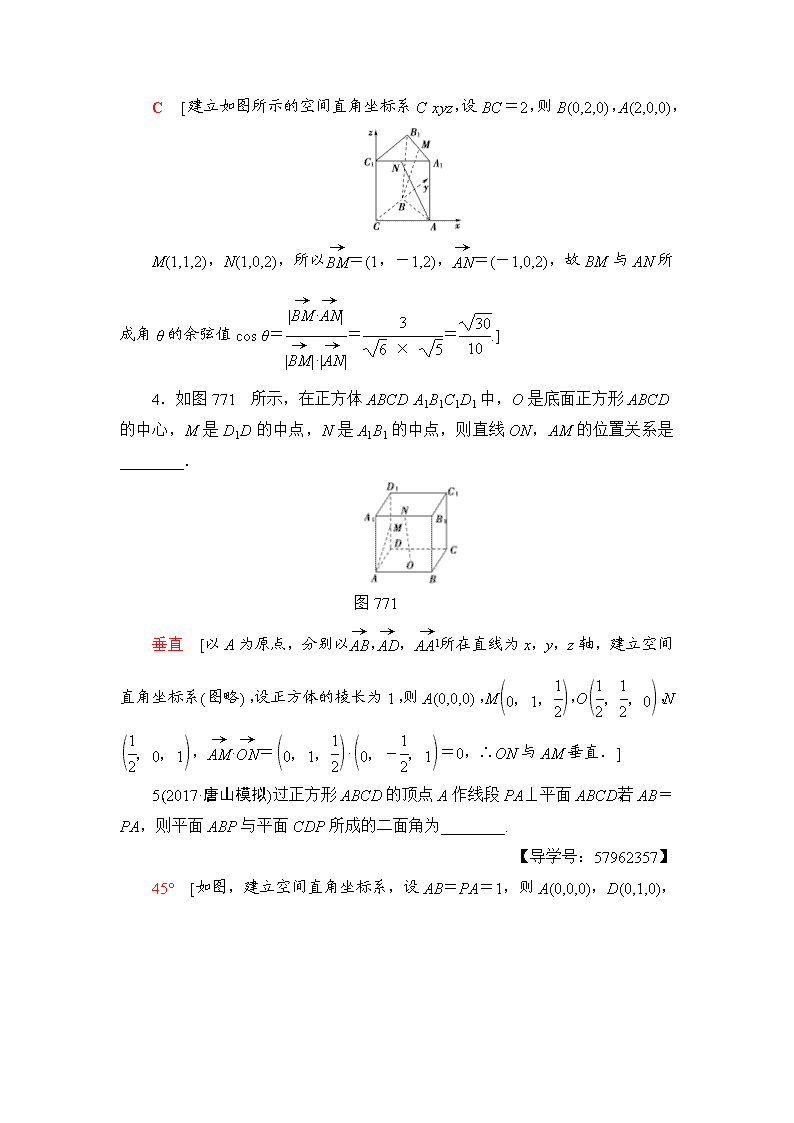D． C　[建立如图所示的空间直角坐标系Cxyz，设BC＝2，则B(0,2,0)，‎ A(2,0,0)，‎ M(1,1,2)，N(1,0,2)，所以＝(1，－1,2)，＝(－1,0,2)，故BM与AN所成角θ的余弦值cos θ＝＝＝.]‎ ‎4．如图771所示，在正方体ABCDA1B1C1D1中，O是底面正方形ABCD的中心，M是D1D的中点，N是A1B1的中点，则直线ON，AM的位置关系是________．‎ 图771‎ 垂直　[以A为原点，分别以，，所在直线为x，y，z轴，建立空间直角坐标系(图略)，设正方体的棱长为1，则A(0,0,0)，M，O，N，·＝·＝0，∴ON与AM垂直．]‎ ‎5．(2017·唐山模拟)过正方形ABCD的顶点A作线段PA⊥平面ABCD，若AB＝PA，则平面ABP与平面CDP所成的二面角为________. ‎ ‎【导学号：57962357】‎ ‎45°　[如图，建立空间直角坐标系，设AB＝PA＝1，则A(0,0,0)，D(0,1,0)，‎ P(0,0,1)，由题意，AD⊥平面PAB，设E为PD的中点，连接AE，则AE⊥PD，又CD⊥平面PAD，‎ ‎∴CD⊥AE，从而AE⊥平面PCD.‎ ‎∴＝(0,1,0)，＝分别是平面PAB，平面PCD的法向量，且〈，〉＝45°.‎ 故平面PAB与平面PCD所成的二面角为45°.]‎ 利用向量证明平行与垂直问题 ‎　如图772所示，在底面是矩形的四棱锥PABCD中，PA⊥底面ABCD，E，F分别是PC，PD的中点，PA＝AB＝1，BC＝2.‎ 图772‎ ‎(1)求证：EF∥平面PAB；‎ ‎(2)求证：平面PAD⊥平面PDC.‎ ‎[证明]　以A为原点，AB，AD，AP所在直线分别为x轴，y轴，z轴，建立空间直角坐标系如图所示，则A(0,0,0)，B(1,0,0)，C(1,2,0)，D(0,2,0)，P(0,0,1)，‎ 所以E，F，＝，＝(0,0,1)，＝(0,2,0)，＝(1,0,0)，＝(1,0,0). 3分 ‎(1)因为＝－，所以∥，即EF∥AB.‎ 又AB平面PAB，EF平面PAB，‎ 所以EF∥平面PAB. 6分 ‎(2)因为·＝(0,0,1)·(1,0,0)＝0，‎ ·＝(0,2,0)·(1,0,0)＝0，‎ 所以⊥，⊥，即AP⊥DC，AD⊥DC. 9分 又因为AP∩AD＝A，AP平面PAD，AD平面PAD，‎ 所以DC⊥平面PAD.‎ 因为DC平面PDC，‎ 所以平面PAD⊥平面PDC. 12分 ‎[规律方法]　1.利用向量证明平行与垂直，充分利用已知的线面垂直关系构建空间直角坐标系，准确写出相关点的坐标，从而将几何证明转化为向量运算．其中灵活建系是解题的关键．‎ ‎2．运用向量知识判定空间位置关系，不可忽视几何定理满足的条件，如用直线的方向向量与平面的法向量垂直来证明线面平行，必需强调直线在平面外．‎ ‎[变式训练1]　(2017·北京房山一模)如图773，四棱锥PABCD的底面为正方形，侧棱PA⊥底面ABCD，且PA＝AD＝2，E，F，H分别是线段PA，PD，AB的中点．‎ 图773‎ 求证：(1)PB∥平面EFH；‎ ‎(2)PD⊥平面AHF.‎ ‎[证明]　建立如图所示的空间直角坐标系Axyz.‎ ‎∴A(0,0,0)，B(2,0,0)，C(2,2,0)，D(0,2,0)，P(0,0,2)，E(0,0,1)，F(0,1,1)，H(1,0,0). 3分 ‎(1)∵＝(2,0，－2)，＝(1,0，－1)，‎ ‎∴＝2，∴PB∥EH.‎ ‎∵PB平面EFH，且EH平面EFH，‎ ‎∴PB∥平面EFH. 6分 ‎(2)＝(0,2，－2)，＝(1,0,0)，＝(0,1,1)，‎ ‎∴·＝0×0＋2×1＋(－2)×1＝0， 9分 ·＝0×1＋2×0＋(－2)×0＝0，‎ ‎∴PD⊥AF，PD⊥AH.‎ 又∵AF∩AH＝A，∴PD⊥平面AHF. 12分 线面角与异面直线所求的角 角度1　求异面直线所成的角 ‎　将正方形ABCD沿对角线AC折起，当以A，B，C，D四点为顶点的三棱锥体积最大时，异面直线AD与BC所成的角为(　　) ‎ ‎【导学号：57962358】‎ A. B. C. D． C　[不妨以△ABC为底面，则由题意当以A，B，C，D为顶点的三棱锥体积最大，即点D到底面△ABC的距离最大时，平面ADC⊥平面ABC.‎ 设点O是AC的中点，连接BO，DO.‎ 则易知BO，CO，DO两两互相垂直．‎ 以O为坐标原点，建立如图所示的空间直角坐标系，令BO＝CO＝DO＝1.‎ 则O(0,0,0)，A(0，－1,0)，D(0,0,1)，B(1,0,0)，C(0,1,0)，‎ 于是＝(0,1,1)，＝(－1,1,0)，‎ 因此cos〈，〉＝＝＝.‎ 所以异面直线AD与BC所成的角为.]‎ ‎[规律方法]　1.利用向量法求异面直线所成的角．‎ ‎(1)选好基底或建立空间直角坐标系；‎ ‎(2)求出两直线的方向向量ν1，ν2；‎ ‎(3)代入公式|cos〈ν1，ν2〉|＝求解．‎ ‎2．两异面直线所成角的范围是θ∈，两向量的夹角α的范围是[0，π]，当异面直线的方向向量的夹角为锐角或直角时，就是该异面直线的夹角；当异面直线的方向向量的夹角为钝角时，其补角才是异面直线的夹角．‎ 角度2　求直线与平面所成的角 ‎　(2015·全国卷Ⅱ)如图774所示，长方体ABCDA1B1C1D1中，AB＝16，BC＝10，AA1＝8，点E，F分别在A1B1，D1C1上，A1E＝D1F＝4.过点E，F的平面α与此长方体的面相交，交线围成一个正方形． ‎ 图774‎ ‎(1)在图中画出这个正方形(不必说明画法和理由)；‎ ‎(2)求直线AF与平面α所成角的正弦值．‎ ‎[解]　(1)交线围成的正方形EHGF如图所示. 5分 ‎(2)作EM⊥AB，垂足为M，则AM＝A1E＝4，EM＝AA1＝8，‎ 因为四边形EHGF为正方形，所以EH＝EF＝BC＝10.‎ 于是MH＝＝6，所以AH＝10.‎ 以D为坐标原点，的方向为x轴正方向，建立如图所示的空间直角坐标系Dxyz，则A(10,0,0)，H(10,10,0)，E(10,4,8)，F(0,4,8)，＝(10,0,0)，＝(0，－6，8). 8分 设n＝(x，y，z)是平面EHGF的法向量，则即 所以可取n＝(0,4,3)．‎ 又＝(－10,4,8)，故|cos〈n，〉|＝＝.‎ 所以AF与平面EHGF所成角的正弦值为. 12分 ‎[规律方法]　1.利用向量法求线面角的方法 ‎(1)分别求出斜线和它在平面内的射影，直线的方向向量，转化为求两个方向向量的夹角(或其补角)．‎ ‎(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余角就是斜线和平面所成的角．‎ ‎2．(1)求直线与平面所成的角，不要误认为是直线的方向向量与平面法向量的夹角．‎ ‎(2)若求线面角的余弦值，要利用平方关系sin2θ＋cos2θ＝1求值.‎ 利用空间向量求二面角 ‎　(2016·全国卷Ⅰ)如图775，在以A，B，C，D，E，F为顶点的五面体中，面ABEF为正方形，AF＝2FD，∠AFD＝90°，且二面角DAFE与二面角CBEF都是60°.‎ 图775‎ ‎(1)证明：平面ABEF⊥平面EFDC；‎ ‎(2)求二面角EBCA的余弦值．‎ ‎[解] (1)证明：由已知可得AF⊥DF，AF⊥FE，‎ 所以AF⊥平面EFDC. 2分 又AF平面ABEF，故平面ABEF⊥平面EFDC. 4分 ‎(2)过D作DG⊥EF，垂足为G.‎ 由(1)知DG⊥平面ABEF.‎ 以G为坐标原点，的方向为x轴正方向，||为单位长，建立如图所示的空间直角坐标系Gxyz. 6分 由(1)知∠DFE为二面角DAFE的平面角，故∠DFE＝60°，则|DF|＝2，|DG|＝，可得A(1,4,0)，B(－3,4,0)，E(－3,0,0)，D(0,0，)．‎ 由已知得AB∥EF，所以AB∥平面EFDC. 8分 又平面ABCD∩平面EFDC＝CD，故AB∥CD，CD∥EF.‎ 由BE∥AF，可得BE⊥平面EFDC，‎ 所以∠CEF为二面角CBEF的平面角，∠CEF＝60°.‎ 从而可得C(－2,0，)．‎ 所以＝(1,0，)，＝(0,4,0)，＝(－3，－4，)，＝(－4,0,0)．‎ 设n＝(x，y，z)是平面BCE的法向量，‎ 则即 所以可取n＝(3,0，－). 10分 设m是平面ABCD的法向量，则 同理可取m＝(0，，4)．‎ 则cos〈n，m〉＝＝－.‎ 故二面角EBCA的余弦值为－. 12分 ‎[规律方法]　1.求解本题要抓住几点：(1)充分利用垂线，建立恰当的直角坐标系；‎ ‎(2)确定二面角DAFE与二面角CBEF的平面角；(3)从空间图形能判定二面角EBCA为钝角．‎ ‎2．利用向量计算二面角大小的常用方法：‎ ‎(1)找法向量法：分别求出二面角的两个半平面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角的大小．‎ ‎(2)找与棱垂直的方向向量法：分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量，则这两个向量的夹角的大小就是二面角的大小．‎ ‎[变式训练2]　 (2017·郑州质检)如图776，在梯形ABCD中，AB∥CD，AD＝DC＝CB＝1，∠BCD＝120°，四边形BFED为矩形，平面BFED⊥平面ABCD，BF＝1.‎ 图776‎ ‎(1)求证：AD⊥平面BFED；‎ ‎(2)点P在线段EF上运动，设平面PAB与平面ADE所成锐二面角为θ ‎，试求θ的最小值. ‎ ‎【导学号：57962359】‎ ‎[解]　(1)证明：在梯形ABCD中，‎ ‎∵AB∥CD，AD＝DC＝CB＝1，∠BCD＝120°，∴AB＝2.‎ ‎∴BD2＝AB2＋AD2－2AB·AD·cos 60°＝3.‎ ‎∴AB2＝AD2＋BD2，∴AD⊥BD. 2分 ‎∵平面BFED⊥平面ABCD，‎ 平面BFED∩平面ABCD＝BD，DE平面BFED，DE⊥DB，‎ ‎∴DE⊥平面ABCD，‎ 则DE⊥AD.‎ 又DE∩BD＝D，∴AD⊥平面BFED. 5分 ‎(2)由(1)知可建立以直线DA，DB，DE为x轴，y轴，z轴的如图所示的空间直角坐标系，令EP＝λ(0≤λ≤)，‎ 则D(0,0,0)，A(1,0,0)，B(0，，0)，P(0，λ，1)，‎ ‎∴＝(－1，，0)，＝(0，λ－，1)．‎ 设n1＝(x，y，z)为平面PAB的法向量，‎ 由得 取y＝1，则n1＝(，1，－λ). 10分 ‎∵n2＝(0,1,0)是平面ADE的一个法向量，‎ ‎∴cos θ＝＝ ‎＝.‎ ‎∵0≤λ≤，∴当λ＝时，cos θ有最大值.‎ ‎∴θ的最小值为. 12分 利用空间向量解决探索性问题 ‎　如图777①所示，正△ABC的边长为4，CD是AB边上的高，E，F分别是AC和BC边的中点，现将△ABC沿CD翻折成直二面角ADCB，如图777②所示．‎ ‎(1)试判断直线AB与平面DEF的位置关系，并说明理由；‎ ‎(2)求二面角EDFC的余弦值；‎ ‎(3)在线段BC上是否存在一点P，使AP⊥DE？证明你的结论．‎ ‎①　　　　　　　　　　　②‎ 图777‎ ‎[解]　(1)如图，在△ABC中，由E，F分别是AC，BC中点，得EF∥AB.‎ 又AB平面DEF，EF平面DEF，‎ ‎∴AB∥平面DEF. 3分 ‎(2)以D为原点，建立如图所示的空间直角坐标系，‎ 则A(0,0,2)，B(2,0,0)，C(0,2，0)，E(0，，1)，F(1，，0)，易知平面CDF的法向量为＝(0,0,2). 5分 设平面EDF的法向量为n＝(x，y，z)，‎ 则即 取n＝(3，－，3)，‎ cos〈，n〉＝＝，‎ ‎∴二面角EDFC的余弦值为. 8分 ‎(3)设P(x，y,0)，则·＝y－2＝0，‎ ‎∴y＝.‎ 又＝(x－2，y,0)，＝(－x,2－y,0)．‎ ‎∵∥，‎ ‎∴(x－2)(2－y)＝－xy，‎ ‎∴x＋y＝2. 10分 把y＝代入上式得x＝，‎ ‎∴＝，‎ ‎∴在线段BC上存在点P，使AP⊥DE. 12分 ‎[规律方法]　1.根据题目的条件进行综合分析和观察猜想，找出点或线的位置，并用向量表示出来，然后再加以证明，得出结论．‎ ‎2．假设所求的点或参数存在，并用相关参数表示相关点，根据线、面满足的垂直、平行关系，构建方程(组)求解，若能求出参数的值且符合该限定的范围，则存在，否则不存在．‎ ‎[变式训练3]　如图778，在长方体ABCD A1B1C1D1中，AA1＝AD＝1，E为CD中点．‎ 图778‎ ‎(1)求证：B1E⊥AD1；‎ ‎(2)在棱AA1上是否存在一点P，使得DP∥平面B1AE？若存在，求AP的长；若不存在，说明理由. ‎ ‎【导学号：57962360】‎ ‎[解]　以A为原点，，，的方向分别为x轴，y轴，z轴的正方向建立如图所示的空间直角坐标系．设AB＝a. 1分 ‎(1)证明：A(0,0,0)，D(0,1,0)，D1(0,1,1)，E，B1(a,0,1)，故＝(0,1,1)，＝. 3分 因为·＝－×0＋1×1＋(－1)×1＝0，‎ 因此⊥，‎ 所以B1E⊥AD1. 5分 ‎(2)存在满足要求的点P，‎ 假设在棱AA1上存在一点P(0,0，z0)，‎ 使得DP∥平面B1AE，此时＝(0，－1，z0)，‎ 再设平面B1AE的一个法向量为n＝(x，y，z)．‎ ＝(a,0,1)，＝. 7分 因为n⊥平面B1AE，所以n⊥，n⊥，得 取x＝1，则y＝－，z＝－a，‎ 则平面B1AE的一个法向量n＝. 10分 要使DP∥平面B1AE，只要n⊥，有－az0＝0，解得z0＝.‎ 所以存在点P，满足DP∥平面B1AE，此时AP＝. 12分 ‎[思想与方法]‎ ‎1．用向量法解决立体几何问题，是空间向量的一个具体应用，体现了向量的工具性，这种方法可把复杂的推理证明、辅助线的作法转化为空间向量的运算，降低了空间想象演绎推理的难度，体现了由“形”转“数”的转化思想．‎ ‎2．用向量来求空间角，都需将各类角转化成对应向量的夹角来计算，问题的关键在于确定对应线段的向量．‎ ‎[易错与防范]‎ ‎1．用向量知识证明立体几何问题，仍然离不开立体几何中的定理．若用直线的方向向量与平面的法向量垂直来证明线面平行，必需强调直线在平面外．‎ ‎2．利用向量求角，一定要注意将向量夹角转化为各空间角．因为向量夹角与各空间角的定义、范围不同．‎ ‎3．求二面角要根据图形确定所求角是锐角还是钝角．‎