安徽省六安市第一中学2019届高三数学下学期模拟考试试题（三）理 21页

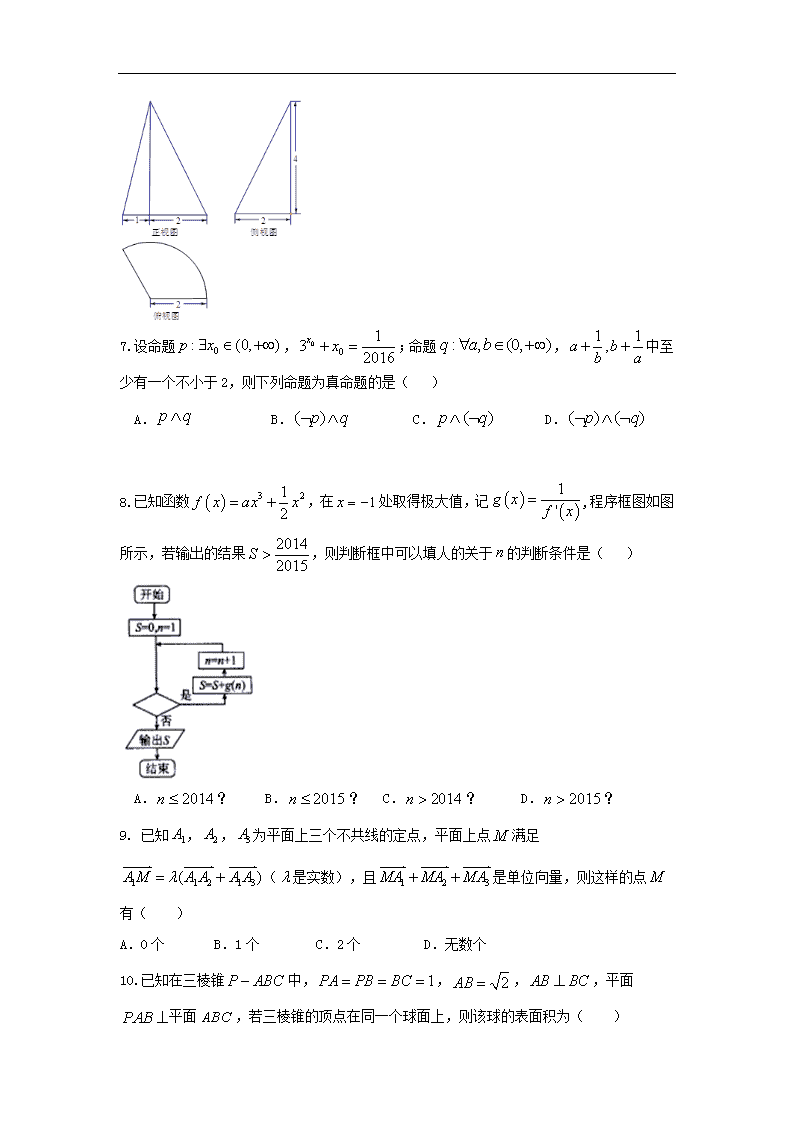
六安一中2019届高考模拟卷 理科数学（三）‎ 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1.“”是“复数（其中是虚数单位）为纯虚数”的（ ）‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎2.若集合，且，则集合可能是（ ）‎ ‎ A. B. C. D.‎ ‎3.等差数列中，是一个与无关的常数，则该常数的可能值的集合为（ ）‎ A． B． C． D．‎ ‎4. 西部某县委将位大学生志愿者(男女) 分成两组, 分配到两所小学支教, 若要求女生不能单独成组, 且每组最多人, 则不同的分配方案共有（ ）‎ A．种 B．种 C．种 D．种 ‎5.已知实数满足，则的取值范围为（ ）‎ A． B． C． D．‎ ‎6.某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（ ）‎ ‎ A. B. C. D.‎ ‎7. 设命题，；命题，中至少有一个不小于2，则下列命题为真命题的是（ ）‎ A． B． C． D．‎ ‎8. 已知函数，在处取得极大值，记,程序框图如图所示，若输出的结果，则判断框中可以填人的关于的判断条件是（ ）‎ A．？ B．？ C．？ D．？‎ ‎9. 已知，，为平面上三个不共线的定点，平面上点满足（是实数），且是单位向量，则这样的点有（ ）‎ A．0个 B．1个 C．2个 D．无数个 ‎10.已知在三棱锥中，，，，平面平面，若三棱锥的顶点在同一个球面上，则该球的表面积为（ ）‎ A． B． C． D．‎ ‎11. 双曲线的左焦点,离心率，过点斜率为的直线交双曲线的渐近线于两点，中点为,若等于半焦距，则等于 （ ）‎ A. B. C. 或 D. ‎ ‎12. 如图，棱长为的正方体，点在平面内，平面与平面所成的二面角为，则顶点到平面的距离的最大值是 （ ）‎ A. B. ‎ C. D.‎ 二、填空题（本大题共4个小题，每小题5分，共20分，把答案填在题中的横线上．）‎ ‎13.的展开式中项的系数为_______.‎ ‎14. 已知某次数学考试的成绩服从正态分布，则114分以上的成绩所占的百分比为 ‎ ‎（附：,‎ ‎)‎ ‎15. 已知为第二象限角，，则的值为 ]‎ ‎16.已知方程有个不同的实数根，則实数的取值范围是 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） ‎ ‎17.（本小题满分12分）‎ 如图，在中，已知点在边上，且，，，.‎ ‎（1）求长； （2）求.‎ ‎18. 如图，在直三棱柱中，平面侧面，且．‎ ‎（1）求证：；‎ ‎（2）若直线与平面所成角的大小为，求锐二面角的大小．‎ ‎19. 某商场计划销售某种产品，现邀请生产该产品的甲、乙两个厂家进场试销10天．两个厂家提供的返利方案如下：甲厂家每天固定返利70元，且每卖出一件产品厂家再返利 ‎2元；乙厂家无固定返利，卖出40件以内（含40件）的产品，每件产品厂家返利4元，‎ 超出40件的部分每件返利6元．分别记录其10天内的销售件数，得到如下频数表：‎ 甲厂家销售件数频数表 销售件数 ‎38‎ ‎39‎ ‎40‎ ‎41‎ ‎42‎ 天数 ‎2‎ ‎4‎ ‎2‎ ‎1‎ ‎1‎ 乙厂家销售件数频数表 销售件数 ‎38‎ ‎39‎ ‎40‎ ‎41‎ ‎42‎ 天数 ‎1‎ ‎2‎ ‎2‎ ‎4‎ ‎1‎ ‎（Ⅰ）现从甲厂家试销的10天中抽取两天，求一天销售量大于40而另一天销售量小于40的概率；‎ ‎（Ⅱ）若将频率视作概率，回答以下问题：‎ ①记乙厂家的日返利额为（单位：元），求的分布列和数学期望；‎ ②商场拟在甲、乙两个厂家中选择一家长期销售，如果仅从日返利额的角度考虑，请利用所学的统计学知识为商场作出选择，并说明理由．‎ ‎20．（本题满分12分）‎ 设椭圆：，其中长轴是短轴长的倍，过焦点且垂直于轴的直线被椭圆截得的弦长为。‎ ‎（I）求椭圆的方程；‎ ‎（II）点是椭圆上动点，且横坐标大于，点，在轴上，‎ 内切于，试判断点的横坐标为何值时的面积最小。‎ ‎21．（本题满分12分）‎ 已知函数．‎ ‎（I）若，求曲线在点处的切线方程；‎ ‎（II）若在处取得极小值，求实数的取值范围．‎ 选修4-4：坐标系与参数方程 ‎22.（本小题满分10分）‎ ‎ 已知曲线E的极坐标方程为，倾斜角为α的直线l过点P (2，2).‎ ‎（1）求曲线E的直角坐标方程和直线的参数方程；‎ ‎ （2）设l1, l2是过点P且关于直线x=2对称的两条直线，l1与E交于A, B两点，l2与E交于C, D两点. 求证：|PA| : |PD|=|PC| : |PB|.‎ 选修4-5：不等式选讲：‎ ‎23．（本小题满分10分）‎ ‎ 设函数 ‎ ‎ （1）若函数f(x)有最大值，求a的取值范围；‎ ‎ （2）若a=1，求不等式f(x)＞|2x-3|的解集 六安一中2019届高考模拟卷 理科数学（三）答案 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1.“”是“复数（其中是虚数单位）为纯虚数”的（ ）‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【答案】B.‎ ‎【解析】‎ 试题分析：由题意得，是纯虚数，故是必要不充分条件，故选B.‎ ‎2.若集合，且，则集合可能是（ ）‎ ‎ A. B. C. D.‎ ‎【答案】A. ‎ ‎【解析】‎ 试题分析：∵，∴，故只有A符合题意，故选A.‎ ‎3.等差数列中，是一个与无关的常数，则该常数的可能值的集合为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】‎ 试题分析：由题意得，因为数列是等差数列，所以设数列的通项公式为，则，所以，因为是一个与 无关的常数，所以或，所以可能是或，故选B.‎ ‎4. 西部某县委将位大学生志愿者(男女) 分成两组, 分配到两所小学支教, 若要求女生不能单独成组, 且每组最多人, 则不同的分配方案共有（ ）‎ A．种 B．种 C．种 D．种 ‎【答案】C ‎【解析】‎ 试题分析：分组的方案有3、4和2、5两类，第一类有种;第二类有种，所以共有N=68+36=104种不同的方案.‎ ‎5.已知实数满足，则的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】‎ 试题分析：作出不等式组不等式的平面区域如图所示，表示的几何意义为区域内的点到点的斜率加上2．因为、，所以，所以由图知或，所以或，即或，故选D．‎ ‎6.某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（ ）‎ ‎ A. B. C. D.‎ ‎【答案】D. ‎ ‎【解析】‎ 试题分析：由题意得，该几何体为底面是一扇形的锥体，∴，故选D.‎ ‎7. 设命题，；命题，中至少有一个不小于2，则下列命题为真命题的是（ ）‎ A． B． C． D．‎ ‎【答案】B 因为在单调递增，所以，假，若都小于2，则，又根据基本不等式可得，矛盾，真 ‎8. 已知函数，在处取得极大值，记,程序框图如图所示，若输出的结果，则判断框中可以填人的关于的判断条件是（ ）‎ A．？ B．？ C．？ D．？‎ ‎【答案】B ‎【解析】‎ 试题分析：，程序框图的作用是求其前项和，由于，故再循环一次就满足，故填.‎ ‎9. 已知，，为平面上三个不共线的定点，平面上点满足（是实数），且是单位向量，则这样的点有（ ）‎ A．0个 B．1个 C．2个 D．无数个 ‎【答案】C.‎ ‎【解析】‎ 试题分析：由题意得，，，，‎ ‎∴，如下图所示，设为的中点，‎ ‎∴与为共起点且共线的一个向量，显然直线与以为圆心的单位圆有两个交点，故这样的点有两个，即符合题意的点有两个，故选C.‎ ‎10.已知在三棱锥中，，，，平面平面，若三棱锥的顶点在同一个球面上，则该球的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】B.‎ ‎【解析】‎ 试题分析：如下图所示，设球心为，则可知球心在面的投影在外心，即中点处，取中点，连，，，，由题意得，面，∴在四边形中，设，∴半径，，即球心即为中点，∴表面积，故选B.‎ ‎11. 双曲线的左焦点,离心率，过点斜率为的直线交双曲线的渐近线于两点，中点为,若等于半焦距，则等于 （ ）‎ A. B. C. 或 D. ‎ 答案：B 分析：与联立，得可求 ‎12. 如图，棱长为的正方体，点在平面内，平面与平面所成的二面角为，则顶点到平面的距离的最大值是 （ ）‎ A. B. C. D.‎ 答案：B 分析：‎ 直线CA在平面上移动， CA与平面所成线面角在变化的过程中，当线面角与二面角重叠时线面角最大。‎ 二、填空题（本大题共4个小题，每小题5分，共20分，把答案填在题中的横线上．）‎ ‎13.的展开式中项的系数为_______.‎ ‎【答案】. ‎ ‎【解析】‎ 试题分析：由二项式定理可知中，，令，可知的系数为，令，可知的系数为，故的展开式中的系数为，故填：.‎ ‎14. 已知某次数学考试的成绩服从正态分布，则114分以上的成绩所占的百分比为 ‎ ‎（附：,‎ ‎)‎ ‎【解析】由已知得，故 ‎15. 已知为第二象限角，，则的值为 ‎ ‎]‎ ‎【解析】由展开得，平方得，所以，从而，因为为第二象限角，故，因此，因为，，所以，，则 ‎16.已知方程有个不同的实数根，則实数的取值范围是 ．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：定义域为，令，这是一个偶函数，我们只需研究上的零点即可，此时，当时，函数单调递增，至多只有一个零点，不合题意；当时，函数在区间上单调增，在区间上单调减，要有两个零点，只需，解得.‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） ‎ ‎17.（本小题满分12分）‎ 如图，在中，已知点在边上，且，，，.‎ ‎（1）求长； （2）求.‎ 试题解析：（1）∵，则，∴，‎ 即，在中，由余弦定理，可知，‎ 即，解得，或，∵，∴；……6分 ‎（2）在中，由正弦定理，可知.‎ 又由，可知，∴.‎ ‎∵，∴.…………12分 ‎ ‎18. 如图，在直三棱柱中，平面侧面，且．‎ ‎（1）求证：；‎ ‎（2）若直线与平面所成角的大小为，求锐二面角的大小．‎ ‎【解析】（1）如图，取的中点，连接.‎ 因为，所以.‎ 由平面侧面，且平面侧面，‎ 得平面. ………………（3分） ‎ 又平面，所以，‎ 因为三棱柱是直三棱柱，则底面，‎ 所以 ‎ 又，从而侧面，又侧面，‎ 故． ………………（6分） ‎ 过点作于点，连接，由（1）知平面，则，又，∴，‎ ‎∴即为二面角的一个平面角. ………………（9分） ‎ 在直角中，，‎ 又，，‎ ‎∴，‎ 又二面角为锐二面角，∴，‎ 即二面角的大小为． ………………（12分） ‎ 解法二（向量法）：由（1）知且底面，所以以点为原点，以所在直线分别为， ，轴建立空间直角坐标系.‎ 设，则，，，，，，，.‎ 设平面的一个法向量，由，，得.‎ 令，得，则. ‎ 设直线与平面所成的角为，则，‎ 所以，‎ 解得， 即． ‎ 又设平面的一个法向量为，同理可得.‎ 设锐二面角的大小为，则，‎ 由，得.‎ ‎∴锐二面角的大小为． ………………（12分） ‎ ‎19. 某商场计划销售某种产品，现邀请生产该产品的甲、乙两个厂家进场试销10天．两个厂家提供的返利方 案如下：甲厂家每天固定返利70元，且每卖出一件产品厂家再返利 ‎2元；乙厂家无固定返利，卖出40件以内（含40件）的产品，每件产品厂家返利4元，‎ 超出40件的部分每件返利6元．分别记录其10天内的销售件数，得到如下频数表：‎ 甲厂家销售件数频数表 销售件数 ‎38‎ ‎39‎ ‎40‎ ‎41‎ ‎42‎ 天数 ‎2‎ ‎4‎ ‎2‎ ‎1‎ ‎1‎ 乙厂家销售件数频数表 销售件数 ‎38‎ ‎39‎ ‎40‎ ‎41‎ ‎42‎ 天数 ‎1‎ ‎2‎ ‎2‎ ‎4‎ ‎1‎ ‎（Ⅰ）现从甲厂家试销的10天中抽取两天，求一天销售量大于40而另一天销售量小于40的概率；‎ ‎（Ⅱ）若将频率视作概率，回答以下问题：‎ ①记乙厂家的日返利额为（单位：元），求的分布列和数学期望；‎ ②商场拟在甲、乙两个厂家中选择一家长期销售，如果仅从日返利额的角度考虑，请利用所学的统计学知识为商场作出选择，并说明理由．‎ ‎（Ⅱ）①设乙产品的日销售量为a，则 当时，；‎ 当时，；‎ 当时，；‎ 当时，；‎ 当时，；‎ ‎∴的所有可能取值为：152,156,160,166,172．……6分 ‎∴的分布列为 ‎152‎ ‎156‎ ‎160‎ ‎166‎ ‎172‎ ‎∴．……… 9分 ②依题意，甲厂家的日平均销售量为：‎ ‎，‎ ‎∴甲厂家的日平均返利额为：元，‎ 由①得乙厂家的日平均返利额为162元（>149元），‎ ‎∴推荐该商场选择乙厂家长期销售．……………………………………… 12分 ‎20．（本题满分12分）‎ 设椭圆：，其中长轴是短轴长的倍，过焦点且垂直于轴的直线被椭圆截得的弦长为。‎ ‎（I）求椭圆的方程；‎ ‎（II）点是椭圆上动点，且横坐标大于，点，在轴上，‎ 内切于，试判断点的横坐标为何值时的面积最小。‎ ‎20. 解: （I）由已知，解得：，故所求椭圆方程为：‎ ‎…………………………3分 ‎（II）设，.不妨设，则直线的 方程为，即，又圆心到 直线的距离为，即，，化简得 ‎，…………………………5分 同理，所以是方程 的两个根，所以，，‎ 则………………………7分 因为是椭圆上的点，所以，，‎ 则，‎ ‎…………………………9分 令，则，令化简 ‎，则，‎ 令，得，而，所以函数在上单调递减，‎ 当即即点的横坐标为时，的面积最小。‎ ‎…………………………12分 ‎21．（本题满分12分）‎ 已知函数．‎ ‎（I）若，求曲线在点处的切线方程；‎ ‎（II）若在处取得极小值，求实数的取值范围．‎ ‎（II）由已知得，则，记，则，……………………5分 ①当，时，，函数单调递增，所以当时，，当时，，所以在处取得极小值，满足题意．……………………7分 ‎②当时，，当时，，故函数单调递增，‎ 可得当时，，时，，所以在处取得极小值，满足题意．‎ ‎………………9分 ‎③当时，当时，， 在内单调递增；时，，在 内单调递减，所以当时，， 单调递减，不合题意．‎ ‎④当时，即 ，当时，，单调递减，，当时，，单调递减，，所以在处取得极大值，不合题意．‎ 综上可知，实数的取值范围为．…………………………12分 ‎22.（本小题满分10分）选修4-4：坐标系与参数方程 ‎ 已知曲线E的极坐标方程为，倾斜角为α的直线l过点P (2，2).‎ ‎（1）求曲线E的直角坐标方程和直线的参数方程；‎ ‎ （2）设l1, l2是过点P且关于直线x=2对称的两条直线，l1与E交于A, B两点，l2与E交于C, D两点. 求证：|PA| : |PD|=|PC| : |PB|.‎ 选修4-5：不等式选讲：‎ ‎23．（本小题满分10分）‎ ‎ 设函数 ‎ ‎ （1）若函数f(x)有最大值，求a的取值范围；‎ ‎ （2）若a=1，求不等式f(x)＞|2x-3|的解集 选修4—4：坐标系与参数方程：‎ ‎22．解：（1）E:x2=4y(x≠0), l: (t为参数) ………5分 ‎ （2）∵l1, l2关于直线x=2对称, ‎ ‎∴l1, l2的倾斜角互补.设l1的倾斜角为α，则l2的倾斜角为π-α,‎ 把直线l1:(t为参数)代入x2=4y并整理得：t2cos2α+4(cosα-sinα)t-4=0,‎ 根据韦达定理，t1t2=,即|PA|×|PB|=.……8分 同理即|PC|×|PD|==.‎ ‎∴|PA|×|PB|=|PC|×|PD|,即|PA | : |PD|=|PC | : |PB|. ……………………10分 选修4—5：不等式选讲：‎ ‎23．解：（1）,………………………2分 ‎ ∵f(x)有最大值，∴1-a≥0且1+a≤0,…………………4分 解得a≤-1.最大值为f(2)=2 ……………5分 ‎ （2）即|x-2|-|2x-3|+x>0.‎ ‎ 设g(x)= |x-2|-|2x-3|+x=, …………7分 ‎ 由g(x)>0解得x>.原不等式的解集为{x|x>}. ………………………10分