四川省绵阳市2020届高三上学期第二次诊断性考试数学（文）试题含答案 11页

874.00 KB
2021-07-01 发布

四川省绵阳市2020届高三上学期第二次诊断性考试数学（文）试题含答案

关闭预览

11页
当前文档由用户上传发布，收益归属用户

1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
网站客服QQ：403074932

秘密★启用前【考试时间：‎2020年1月5日l5：00-17: 00】‎ 绵阳市高中2017级第二次诊断性考试文科数学一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．设全集U= {x|x>0}，M={x|l0，b>0）的右焦点为F，过F作与双曲线的两条渐近线平行的直线且与渐近线分别交于A，B两点，若四边形OAFB (O为坐标原点)的面积为bc，则双曲线的离心率为 ‎ A. B‎.2 C. D.3‎ ‎10.已知圆C：x2+y2 -2x-8=0，直线l经过点M(2，2)，且将圆C及其内部区域分为两部分，则当这两部分的面积之差的绝对值最大时，直线l的方程为 ‎ A. x-2y+2=0 B. 2x+y-6=‎0 C.2x-y-2=0 D. x+2y-6=0‎ ‎11.己知f(x)为偶函数，且当x≥0时，，则满足不等式 f(log‎2m)+f()< ‎2f (1)的实数m的取值范围为 ‎ A．（，2） B．(0，2) C．(0，)∪(1，2) D．(2，+∞)‎ ‎12．函数f(x)=(2ax-1)2 -loga(ax+2）在区间[0， ]上恰有一个零点，则实数a的取值范围是 ‎ A.( ， ) B. 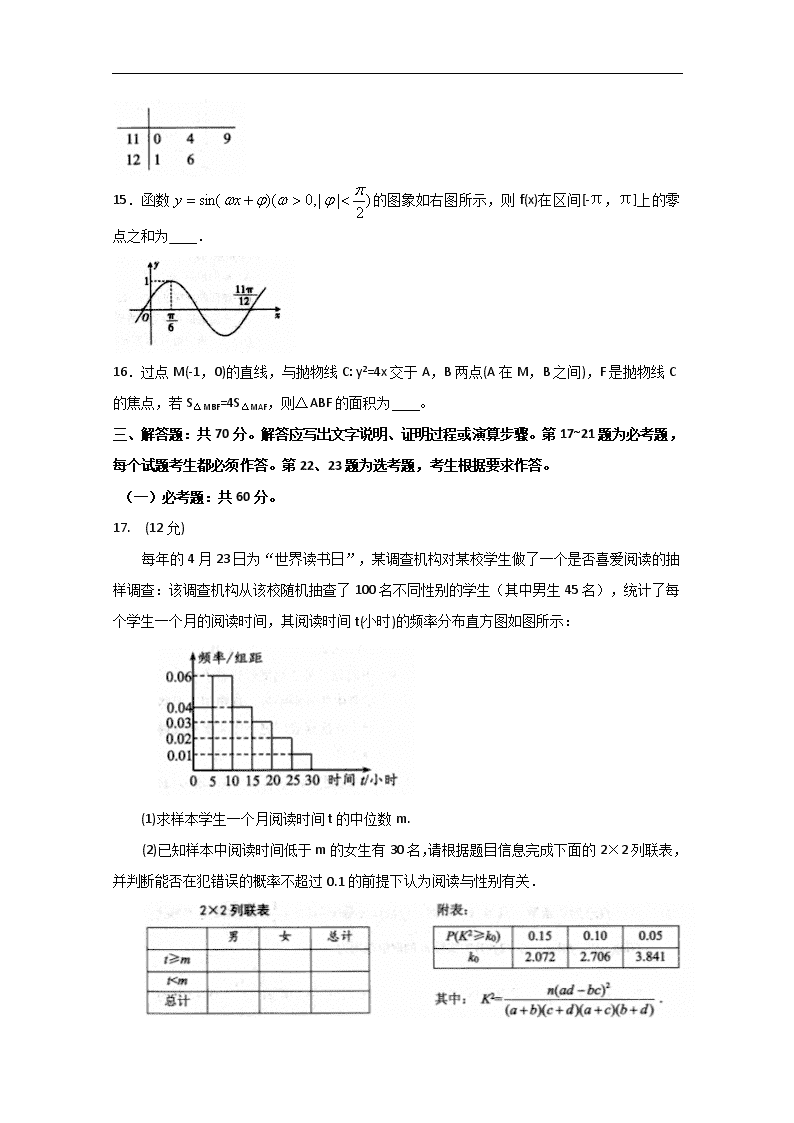(1,2] ∪ [3,+∞) C.(1,2) ∪[3, +∞) D.[2,3)‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13．直线l1：ax-(a+l)y-1=0与直线4x-6y+3=0平行，则实数a的值是．‎ ‎14.某同学在最近的五次模拟考试中，其数学成绩的茎叶图如右图所示，则该同学这五次数学成绩的方差是____．‎ ‎15．函数的图象如右图所示，则f(x)在区间[-π，π]上的零点之和为____．‎ ‎16．过点M(-1，0)的直线，与抛物线C: y2=4x交于A，B两点(A在M，B之间)，F是抛物线C的焦点，若S△MBF=4S△MAF，则△ABF的面积为。‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎ （一）必考题：共60分。‎ ‎17. (12允)‎ 每年的‎4月23日为“世界读书日”，某调查机构对某校学生做了一个是否喜爱阅读的抽样调查：该调查机构从该校随机抽查了100名不同性别的学生（其中男生45名），统计了每个学生一个月的阅读时间，其阅读时间t(小时)的频率分布直方图如图所示： ‎ ‎ ‎ ‎ (1)求样本学生一个月阅读时间t的中位数m.‎ ‎(2)已知样本中阅读时间低于m的女生有30名，请根据题目信息完成下面的2×2列联表，并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关．‎ ‎ 18．(12分)‎ ‎ 已知等差数列{an}的公差d=2，a3>0，且-3为a4与a7的等比中项．数列{bn}的通项公式为bn=.‎ ‎(1)求数列{bn}的通项公式；‎ ‎(2)记 (n∈N*)，求数列{cn}的前n项和Sn.‎ ‎19. (12分)‎ ‎ 在△ABC中，内角A，B，C所对的边分别为a，b，c. 已知(sinA+sinB)(a -b) =c(sinC+sinB).‎ ‎ (l)求A；‎ ‎(2)若D为BC边上一点，且AD⊥BC, BC=2AD，求sinB．‎ ‎20．(12分)‎ ‎ 已知椭圆C：,动直线l过定点(2，0)且交椭圆C于A，B两点(A，A不在x轴上）．‎ ‎ (l)若线段AB中点Q的纵坐标是-，求直线l的方程；‎ ‎(2)记A点关于x轴的对称点为M,若点N（n，0）满足，求n的值．‎ ‎ ‎ ‎21．(12分)‎ 己知函数f(x) =2lnx+x2-ax，其中a∈R．‎ ‎ (1)讨论函数f(x)的单调性；‎ ‎ (2)若a≥3，记函数f(x)有两个极值点xl，x2(其中x2>x1)，求 f(x2)-f(xI)的最大值．‎ ‎ ‎ ‎（二）选考题：共10分。请考生在第22、23题申任选一题做答。如果多做，则按所做的 ‎ 第一题计分。‎ ‎ 22.[选修4-4：坐标系与参数方程】（10分）‎ 在平面直角坐标系中，曲线C1的参数方程为（r>0，为参数），以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C1经过点P(2，)，曲线C2的直角坐标方程为x2-y2=1．‎ ‎ (1)求曲线C1的普通方程，曲线C2的极坐标方程；‎ ‎(2)若A(ρ1，α)，B(ρ2，α-)是曲线C2上两点，当α∈(0，)时，求的取值范围．‎ ‎23.【选修4-5：不等式选讲】（10分）‎ ‎ 已知关于x的不等式|x+l|-|2x-l|≤，其中a>0．‎ ‎(1)当a=4时，求不等式的解集；‎ ‎(2)若该不等式对x∈R恒成立，求实数a的取值范围．‎

四川省绵阳市2020届高三上学期第二次诊断性考试数学（文）试题含答案 11页