2020_2021学年新教材高中数学第五章三角函数5 49页

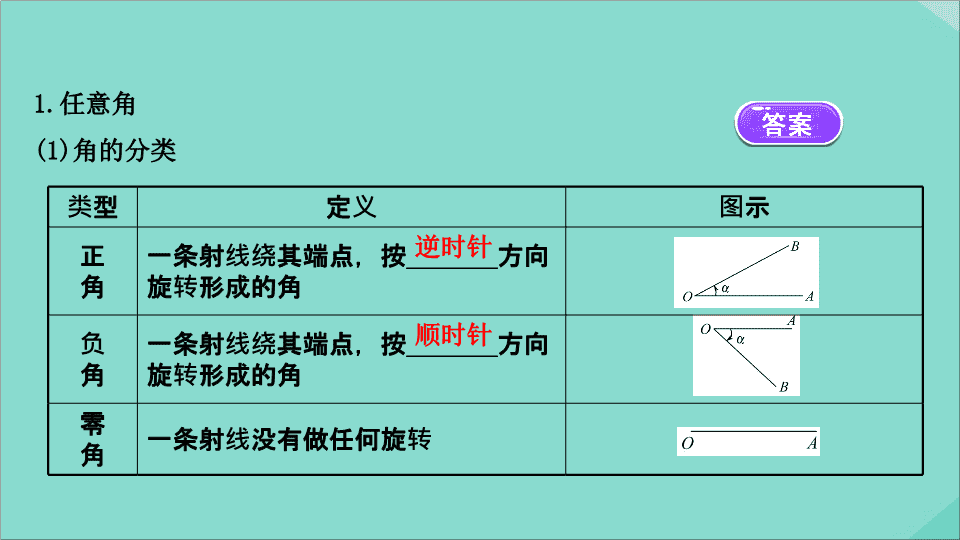
5.1.1 　任　意　角 必备知识 · 自主学习 导思 1. 体操中“前空翻转体 540 度” “后空翻转体 720 度”是什么意思？ 2. 任意角可以分为哪几类？ 3. 什么是终边相同的角？ 1. 任意角 (1) 角的分类 类型 定义 图示 正 角 一条射线绕其端点，按 _______ 方向旋转形成的角 负 角 一条射线绕其端点，按 _______ 方向旋转形成的角 零 角 一条射线没有做任何旋转 逆时针 顺时针 (2) 本质：将初中所学的锐角、直角、钝角、平角和周角等推广到任意角 . (3) 应用：可以定义任意的旋转角 . 2. 象限角 如果角的顶点与坐标原点重合，角的始边与 x 轴的 _________ 重合，那么，角的 终边 ( 除端点外 ) 在第几象限，就说这个角是 ___________. 如果角的终边在坐标 轴上，就认为这个角不属于任何一个象限 . 3. 终边相同的角 (1) 定义：所有与角 α 终边相同的角，连同角 α 在内 . (2) 表示：集合 S={β|β=α+k·360° ， k∈Z}. (3) 本质：表示成角 α 与整数个周角的和 . 非负半轴 第几象限角 【 思考 】 反过来，若角 α ， β 满足 S={β|β=α+k·360° ， k∈Z} 时，角 α ， β 是否是终边相同的角？ 提示： 当角 α ， β 满足 S={β|β=α+k·360° ， k∈Z} 时，表示成角 α 与 β 相隔整数个周角，即角 α ， β 终边相同 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”，错的打“ ×”) (1) 经过 1 小时，时针转过 30°. ( 　　 ) (2) 终边与始边重合的角是零角 . ( 　　 ) (3) 第二象限的角是钝角 . ( 　　 ) 提示： (1)× ，因为是顺时针旋转，所以时针转过 -30°. (2)× ，终边与始边重合的角是 k·360°(k∈Z). (3)× ，钝角是第二象限的角，但第二象限角不一定是钝角 . 2. 与 45° 角终边相同的角是 ( 　　 ) A.-45° 　　　 B.225° 　　　 C.395° 　　　 D.-315° 【 解析 】 选 D. 与 45° 角终边相同的角可以表示为 45°+k·360° ， k∈Z ，结合四个选项可以发现只有答案 D 符合题意 . 3.( 教材二次开发：例题改编 ) 已知 0°≤α<360° ，且 α 与 600° 角终边相同，则 α=_______ ，它是第 _______ 象限角 .  【 解析 】 因为 600°=360°+240° ，所以 240° 角与 600° 角终边相同，且 0°≤240°<360° ，故 α=240° ，它是第三象限角 . 答案： 240° 　三 关键能力 · 合作学习 类型一　任意角的概念及应用 ( 数学抽象 ) 【 题组训练 】 1.(2020· 杭州高一检测 ) 下列说法：①终边相同的角必相等；②锐角必是第一象限角；③小于 90° 的角是锐角；④第二象限的角必大于第一象限的角；⑤若角 α 的终边经过点 M(0 ， -3) ，则角 α 是第三或第四象限的角，其中错误的是 ( 　　 ) A.③④⑤ 　 B.①③④ 　 C.①③④⑤ 　 D.②③④⑤ 2. 给出下列四个命题：① -75° 是第四象限角；② 225° 是第三象限角；③ 475° 是第三象限角；④ -310° 是第一象限角 . 其中正确的命题有 ( 　　 ) A.1 个 B.2 个 C.3 个 D.4 个 3. 将时钟拨快 20 分钟，则分针转过的度数是 _______.  【 解析 】 1. 选 C.① 终边相同的角必相等错误，如 0° 与 360° 终边相同，但不相等； ②锐角的范围为 (0° ， 90°) ，必是第一象限角，正确； ③小于 90° 的角是锐角错误，如负角； ④第二象限的角必大于第一象限的角错误，如 120° 是第二象限角， 390° 是第一象限角； ⑤若角 α 的终边经过点 M(0 ， -3) ，则角 α 是终边在 y 轴负半轴上的角，故⑤错误 . 其中错误的是①③④⑤ . 2. 选 C. 因为 -90°<-75°<0° ，所以 -75° 是第四象限角，正确；因为 180°<225°<270° ，所以 225° 是第三象限角，正确； 因为 360°+90°<475°<360°+180° ，所以 475° 是第二象限角，错误；因为 -360°<-310°<-270° ，所以 -310° 是第一象限角，正确 . 所以这四个命题中有 3 个是正确的 . 3. 分针每分钟转 6° ，由于顺时针旋转，所以 20 分钟转了 -120°. 答案： -120° 【 解题策略 】 根据角的概念解题的关键 (1) 准确理解各个象限内角的特点，逐个判断所在的象限 . (2) 钟表的旋转方向都是顺时针方向，所以所得的角应该是负角 . 【 补偿训练 】 已知集合 A={ 第一象限角 } ， B={ 锐角 } ， C={ 小于 90° 的角 } ，则下面关系正确的是 ( 　　 ) A.A=B=C 　　　　　 B.A ⊆ C C.A∩C=B D.B∪C ⊆ C 【 解析 】 选 D. 由已知得 B ⊆ C ，所以 B∪C=C ，故 D 正确 . 类型二　终边相同的角的表示及应用 ( 直观想象 ) 【 典例 】 写出终边落在直线 y=x 上的角的集合 S ，并把 S 中适合不等式 -360°≤β<720° 的元素 β 写出来 . 四步 内容 理解 题意 条件：角的终边在直线 y=x 上 . 结论：①求角的集合； ②求适合 -360°≤β<720° 的角 . 思路 探求 ① 在 0° ～ 360° 内找到终边在 y=x 上的角； ②推广到任意角； ③找出 -360°≤β<720° 内的角 . 四步 内容 书写 表达 直线 y=x 与 x 轴的夹角是 45° ，在 0° ～ 360° 范围内，终边在直线 y=x 上的角有两个： 45° ， 225°. ① 因此，终边在直线 y=x 上的角的集合： S={β|β=45°+k·360° ， k∈Z}∪{β|β=225°+k·360° ， k∈Z} ={β|β=45°+2k·180° ， k∈Z}∪{β|β=45°+(2k+1)·180° ， k∈Z}={β|β=45°+n·180° ， n∈Z}. ② 所以 S 中适合 -360°≤β<720° 的元素是： 45°-2×180°=-315° ； 45°-1×180°=-135° ； 45°+0×180°=45° ； 45°+1×180°=225° ； 45°+2×180°=405° ； 45°+3×180°=585°. 注意解题过程的规范性： ①终边在直线 y=x 上注意讨论两种情况 . ② 这种形式的两个集合取并集时合并为一个集合 . 四步 内容 题后 反思 在 0° ～ 360° 范围内，终边在 y=x 上的角有两个，这是同学们容易忽视的地方；最后在 -360° ～ 720° 求角时，要适当选取 k 的值 . 【 解题策略 】 (1) 一般地，可以将所给的角 β 化成 k·360°+α 的形式 ( 其中 0°≤α<360° ， k∈Z) ，其中的 α 就是所求的角 . (2) 如果所给的角的绝对值不是很大，可以通过如下方法完成：当所给角是负角时，采用连续加 360° 的方式；当所给角是正角时，采用连续减 360° 的方式，直到所得结果达到要求为止 . 特别提醒：表示终边相同的角时， k∈Z 这一条件不能省略 . 【 跟踪训练 】 1.(2020· 济南高一检测 ) 下列各角中，与角 30° 终边相同的角是 ( 　　 ) A.-390° 　　　　　　 B.-330° C.330° D.570° 【 解析 】 选 B. 与角 30° 终边相同的角的集合为 {α|α=30°+k·360° ， k∈Z} ， 取 k=-1 ，可得 α=-330° ， 所以与角 30° 终边相同的角是 -330°. 2. 写出终边落在 x 轴上的角的集合 S. 【 解析 】 S={α|α=k·360° ， k∈Z}∪{α|α=k·360°+180° ， k∈Z} ={α|α=2k·180° ， k∈Z}∪{α|α=(2k+1)·180° ， k∈Z} ={α|α=n·180° ， n∈Z}. 【 拓展延伸 】 运用终边相同的角的注意点 　　　所有与角 α 终边相同的角，连同角 α 在内可以用式子 k·360°+α ， k∈Z 表示，在运用时需注意以下四点： (1)k 是整数，这个条件不能漏掉 . (2)α 是任意角 . (3)k·360° 与 α 之间用“ +” 连接，如 k·360°-30° 应看成 k·360°+(-30°) ， k∈Z. (4) 终边相同的角不一定相等，但相等的角终边一定相同，终边相同的角有无数个，它们相差周角的整数倍 . 【 拓展训练 】 　写出与 α=-1 910° 终边相同的角的集合，并把集合中适合不等式 -720°≤β<360° 的元素 β 写出来 . 【 解析 】 与 α=-1 910° 终边相同的角的集合为 {β|β=k·360°-1 910° ， k∈Z}. 因为 -720°≤β<360° ，即 -720°≤k·360°-1 910°<360°(k∈Z) ， 所以 3 ≤k<6 (k∈Z) ，故取 k=4 ， 5 ， 6. k=4 时， β=4×360°-1 910°=-470° ； k=5 时， β=5×360°-1 910°=-110° ； k=6 时， β=6×360°-1 910°=250°. 类型三　象限角及其应用 ( 直观想象 ) 　角度 1 　用不等式组表示角的集合  【 典例 】 如图所示 . (1) 写出终边落在射线 OA ， OB 上的角的集合 . (2) 写出终边落在阴影部分 ( 包括边界 ) 的角的集合 . 【 思路导引 】 (1) 根据题目给出的角度分别写出 OA ， OB 表示的角 . (2) 根据阴影部分写出不等式，注意两个角的先后顺序 . 【 解析 】 (1) 终边落在射线 OA 上的角的集合是 {α|α=k·360°+210° ， k∈Z}. 终边落在射线 OB 上的角的集合是 {α|α=k·360°+300° ， k∈Z}. (2) 终边落在阴影部分 ( 含边界 ) 的角的集合是 {α|k·360°+210°≤α≤k·360°+300° ， k∈Z}. 【 变式探究 】 如图所示，写出终边落在阴影部分的角的集合 . 【 解析 】 设终边落在阴影部分的角为 α ，角 α 的集合由两部分组成 . ①{α|k·360°+30°≤α