七年级下数学课件《探索直线平行的性质》 (2)_苏科版 16页

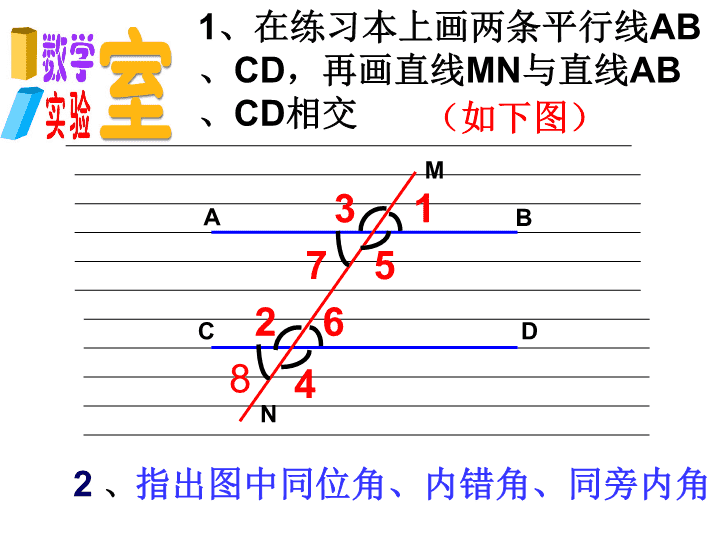
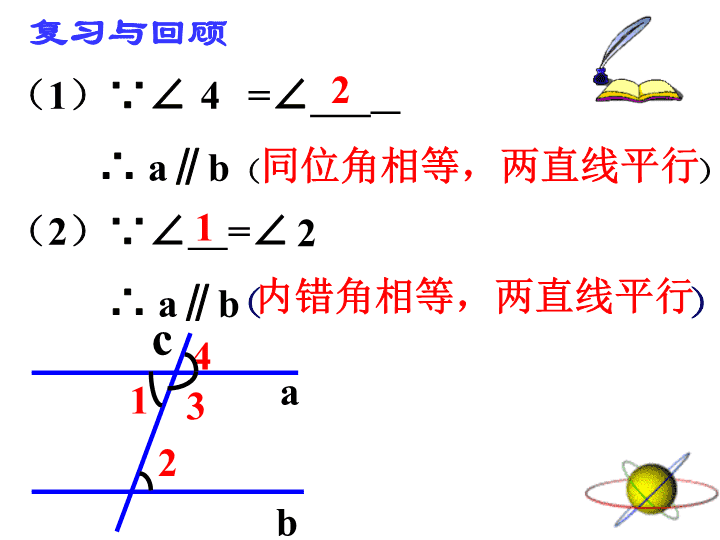
A B C D M N 1、在练习本上画两条平行线AB、 CD，再画直线MN与直线AB、 CD相交 2 、指出图中同位角、内错角、同旁内 角 13 6 8 2 57 4 （如下图） （ ） 复习与回顾 （1）∵∠ =∠___ ∴ a∥b（ ） （2）∵∠ =∠ ∴ a∥b 1 2 2 4 同位角相等，两直线平行 内错角相等，两直线平行 c b 4 3 2 1 a （ ） （3）∵∠ +∠ =180° ∴ a∥b 23 同旁内角互补，两直线平行 复习与回顾 4 3 2 1 a c b 7 2 5 6 3 1 8 4 2、将上图按照如下方式剪开，并分别 把剪开得到的每对同位角、内错角重叠， 你发现了什么？ 做 一 做  2、将上图按照如下方式剪开，并分别 把剪开得到的每对同位角重叠，你发现 了什么？ 做 一 做  7 2 5 6 两直线平行,同位角相等 哇！我有发现啦！ 3 1 8 4 2、将上图按照如下方式剪开，并分别 把剪开得到的每对 重叠，你发现 了什么？ 做 一 做  8 4 7 2 5 6 3 1 两直线平行,内错角相等 哇！我又 知道啦！ 内错角 你能根据”两直线平行,同位角 相等”,说明“两直线平行,内错 角相等”成立的理由吗? a b c1 2 3 解： ∵a∥b ∴∠1=∠2 如图所示 又∵ ∠1=∠3（对顶角相等） （已知） （两直线平行,内错角相等） ∴∠2=∠3 (等量代换) 做 一 做  7 2 5 6 3、将图中的每对同旁内角剪成两部分，并 把他们拼到一起去，你发现每对同旁内角 之间有什么关系？ 两直线平行,同旁内角互补. 哇！请注意，我 又有 新发现啦！ 7 3 1 8 4 2 如果我们现在只知道”两 直线平行,同位角相等”.你能 说明两直线平行,同旁内角互 补”成立的理由吗? ∴ ∠2 + ∠3 = 180° 解：如图所示 1 a3 2 b∵a∥b (已知) ∴∠1=∠2 (两直线平行,同位角相等) 又∵ ∠1+∠3 = 180° (平角定义) (等量代换) 例1 已知:直线a∥b,c∥d, ∠1=115°, 求∠2与∠3的度数 解： ∵ a∥b ∴∠2＝∠1＝115° ∵ c∥d ∴∠3＝∠2＝115° （两直线平行，内错角相等） （已知） （已知） （两直线平行，内错角相等） 1 2 3 a b c d 1.如图若AB ∥ CD,则下列结论中 ① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B ④ ∠B + ∠BCD= 180°正 确的 是 ( ) A ① ② B ① ③ C ① ④ D ③ ④ D A B EC D 1 2 3 × √ × √ 2.如图,若AB ∥ ED,BC ∥ FE, 则∠B + ∠E=_______ A B C D EF °180 例3 如图,AD∥BC, ∠A=∠C. 试说明AB∥DC A E F CB D (同位角相等,两直线平行) 解: ∵AD∥BC(已知) ∴∠C=∠CDE (两直线平行,内错角相等) 又∵ ∠A=∠C(已知) ∴ ∠A=∠CDE (等量代换) ∴AB∥DC A B C D 21 例2 如图:已知AB∥CD,求 ∠A+∠B+∠ACB的度数. 解：因为AB∥CD，根据“两直线 平行，内错角相等” 所以∠A＝∠1. 因为AB∥CD，根据“两直线平 行，同位角相等” 所以∠B＝∠2. 所以 ∠ A+∠B+∠ACB = ∠1+ ∠2+ ∠ACB= 180° 课堂小结： 通过本节课的学习，你有什么感悟？ (1)平行线的三条性质 (2)利用平行线的三条性质解计算题和简单 的解答题 作业: P14 -15 1～4