七年级下册数学课件《平方差公式 平方差公式的应用》 (6)_北师大版 13页

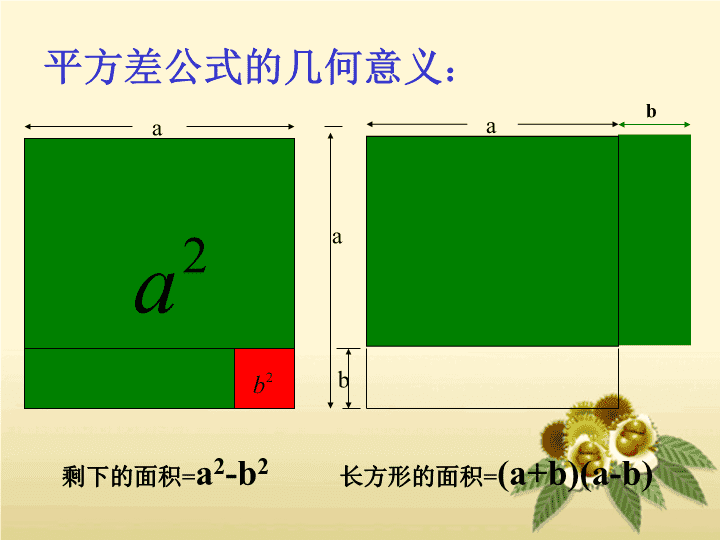
学习目标：1.了解平方差公式的几何背景，发展几何直观2.会用平方差公式进行计算 知识回顾:1、平方差公式？2、公式的结构特点是什么？ aba长方形的面积=(a+b)(a-b)剩下的面积=a2-b2ab平方差公式的几何意义： 练习1：判断下列式子是否正确，错误的并改正(1)(2y+3x)(3x-2y)=4y2-9x2()(2)(5xy+1)(-1+5xy)=25x2y2-1()(3)(m+2n)(m-2n)=m2-2n2()(4)(x-1)(-1-x)=x2-1()(5)(mn+1)(mn-1)=mn2-1()(6)(-2x+3y)(3y-2x)=9y2-4x2（）×××××√ 练习2：用平方差公式直接写出答案：（3b－2a）（2a+3b）（-2a＋3b）（-2a－3b）（3b＋2a）（2a－3b）（-2a－3b）（2a－3b） (1)计算下列各组算式7×9=8×8=想一想11×13=12×12=79×81=80×80=(2)你发现了什么规律？7×9=8×8-111×13=12×12-179×81=80×80-1 例3用平方差公式进行计算：（1）103×97（2）118×122=（100+3）（100-3）=（120-2）（120+2）=1002-9=1202-4=14400-4=14396=9991 例4计算：(2)(2x-5)(2x+5)-2x(2x-3)(1)a2(a+b)(a-b)+a2b2=4x2-25-4x2+6x=6x-25=a2(a2-b2)+a2b2=a4-a2b2+a2b2=a4 (3)(a-b)(a+b)-(3a+2b)(3a-2b)(4)20042－2005×2003=a2-b2-(9a2-4b2)=-8a2+3b2=a2-b2-9a2+4b2=20042－(2004+1)(2004－1)=20042－20042+1=1 1、（x－1）(x2+1)(x+1)2、(a－3)(a+4)(a+3)(a－4)3、(2a－5b)(2a+5b)(4a2+25b2)挑战自我 拓展延伸计算（用指数形式表示）1、（x-1）(x+1)(x2+1)(x4+1)(x8+1)(x16+1)2、(2+1)(22+1)(24+1)(28+1)(216+1) 课堂小结：本节课你学到了什么？ 作业1.教材习题1.102.拓展作业：3.补充题(21+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1)