七年级上册数学课件《有理数的乘方》 (6)_北师大版 (2) 16页

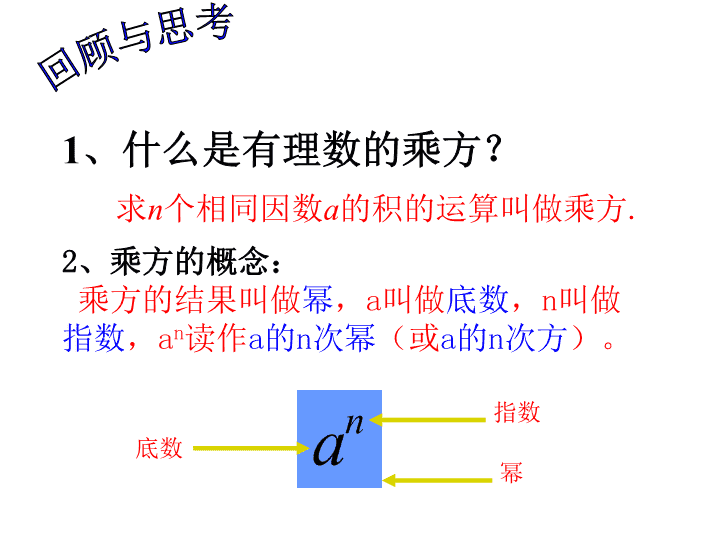
第二章有理数及其运算有理数的乘方（2） 回顾与思考1、什么是有理数的乘方？求n个相同因数a的积的运算叫做乘方.2、乘方的概念：乘方的结果叫做幂，a叫做底数，n叫做指数，an读作a的n次幂（或a的n次方）。底数指数幂 棋盘摆米古时候,有个王国里有一位聪明的大臣，他发明了国际象棋，献给了国王，国王从此迷上了下棋。为了对聪明的大臣表示感谢，国王答应满足这个大臣的一个要求。大臣说：“就在这个棋盘上放一些米粒吧。第1格放1粒，第2格放2粒米，第3格放4粒米，然后是8粒、16粒、32粒……一直到第64格。”“你真傻！就要这么一点米？”，国王哈哈大笑。这位大臣说：“就怕您的国库里没有这么多米！”故事你认为国王的国库里有这么多米吗？ 故事解答：同学现在可以估计国王的国库有没有这么多米粒？（小组讨论）放满64格子一共需要：1+2+22+23+…+263同学们知道264-1=18446744073709551615有多大吗？这些米粒有多少千克？=264-1=18446744073709551615 解:(1)102=10×10=100103=10×10×10=1000,104=10×10×10×10=10000;105=10×10×10×10×10=100000(2)(-10)2=（-10）×（-10）＝100.例3计算：(1)102,103,104，105;(2)(-10)2,(-10)3,(-10)4,(-10)5.(-10)3=（-10）×（-10）×（-10）＝-1000.(-10)4=（-10）×（-10）×（-10）×（-10）＝10000.（-10）5=（-10）×（-10）×（-10）×（-10）×（-10）＝-100000.自主学习、整体感知 解:(1)102=100,103=1000,104=10000，105=100000;(2)(-10)2=100,(-10)3=-1000,(-10)4=10000，(-10)5=-100000.例3计算：想一想:观察例3的结果,你能发现什么规律?与同伴进行交流。 注意:(1)负数的乘方,在书写时一定要把整个负数(连同符号),用小括号括起来.观察例3的结果,我能发现出这样的规律：（1）正数的任何次方都是正数；负数的偶次方是正数，负数的奇次方是负数。（2）10的n次方等于1的后面有n个0。反过来，1的后面有n个0这个数可以写成10的n次方。(2)分数的乘方,在书写的时一定要把整个分数用小括号括起来. (1)（-1/3）2（2）-(1/3)2（3）-32x23（4）（-3）2x（-2）3（5）-2x32（6）（-2x3）2演练提高 解答过程：(1)（-1/3）2=（-1/3）x（-1/3）=1/9（2）-(1/3)2=-(1/3)x(1/3)=-1/9（3）-32x23=-(3x3)x(2x2x2)=-72（4）（-3）2x（-2）3=(-3)x(-3)x(-2)x(-2)x(-2)=-72（5）-2x32=-2x(3x3)=-18（6）（-2x3）2=(-6)2=36 反思较为复杂的乘方运算要特别注意括号和运算顺序，括号和运算顺序不同，结果不同。 每层楼房平均高度为3米，这张纸对折20次后有多少层楼高？1.有一张厚度是0.1毫米的纸，将它对折1次后，厚度为2×0.1毫米。（1）对折2次后，厚度为多少毫米？（2）对折20次后，厚度为多少毫米？1次2次20次合作交流、情境探究 解:(1)2×2×0.1=22×0.1=0.4(毫米)(2)220×0.1=104857.6×0.1=104857.6(毫米)对折20次后的纸有:104857.6÷1000÷3=34.95≈35(层)楼那么高。活动体会：当底数大于1时，随着次数的增加，乘方的结果以惊人的速度增加。 2.你见过拉面师傅拉面条吗？拉面师傅将一根粗面条拉长、俩头捏合，再拉长、捏合，重复这样，就拉成许多根细面条啦。师傅拉1次得到几根面条？2次呢？3次呢？4次呢？在一次比赛中，某拉面师傅用1kg面粉拉出约209万根面条，猜一猜他拉了几次就得到这个结果？210220221=1024=1048576=2097152答案：拉21次 课内检测课本随堂练习第1、2题 1、一个大于1的数作底数，指数越大，乘方的结果，2、较为复杂的乘方运算要特别注意括号和运算顺序，括号和运算顺序不同，结果就不同。越大我们来小结一下： 作业：1、习题2.14（P61-62）第1题第2题2、课堂精炼《有理数的乘方》二课时下课了!