七年级下册数学课件《认识三角形 三角形的三边关系》 (7)_北师大版 27页

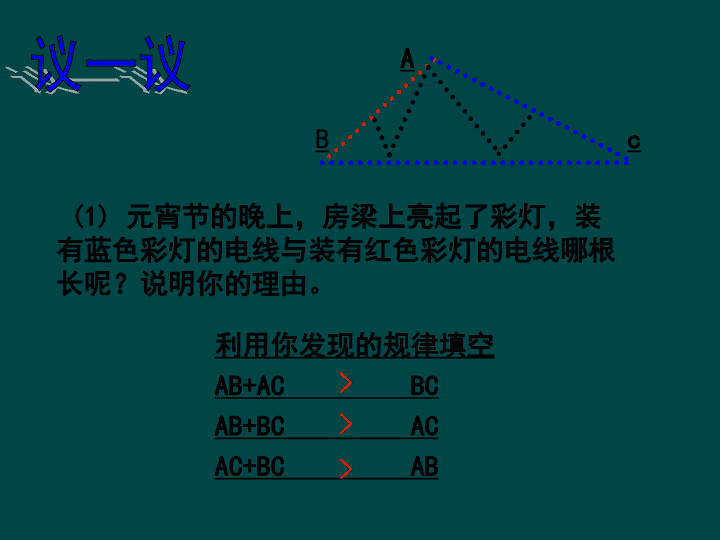
三角形的三边关系 (1)元宵节的晚上，房梁上亮起了彩灯，装有蓝色彩灯的电线与装有红色彩灯的电线哪根长呢？说明你的理由。利用你发现的规律填空AB+ACBCAB+BCACAC+BCABABc>>>议一议 ABc想一想在一个三角形中,任意两边之和与第三边的长度有怎样的关系? 在A点的小狗，为了尽快吃到B点的肉骨头，它选择A—B路线，而不选择A—C—B路线，由此你能得到什么结论？CBA想一想三角形任意两边之和大于第三边 人行横道.A.B想一想横穿马路是一种不文明的行为，从A点到B点为什么还经常有行人斜穿马路而不走人行横道？ 人行横道.A.B想一想2.两点之间的所有连线中，线段最短1.三角形任意两边之和大于第三边 任意做两个三角形，量出它们每条边的长，计算每个三角形的任意两边之差，并与第三边比较，你能得到什么结论？三角形任意两边之差小于第三边做一做 例１：有两根长度分别为5cm和8cm的木棒，用长度为2cm的木棒与它们能摆成三角形吗？为什么？长度为13cm的木棒呢？动手摆一摆。做一做 解：取长度为2cm的木棒时，由于2+5=7<8，出现了两边之和小于第三边的情况，所以它们不能摆成三角形。取长度为13cm的木棒时，由于5+8=13，出现了两边之和等于第三边的情况，所以它们也不能摆成三角形。做一做 下列长度的三条线段能否组成三角形？为什么？（1）3，4，8（）（2）2，5，6（）（3）5，6，10（）（4）3，5，8（）不能能能不能练一练 判断三条线段能否组成三角形，是否一定要检验三条线段中任何两条的和都大于第三条？有没有更简便的判断方法？窍门：用较短的两条线段之和与最长的线段比较，若和大，能组成三角形，反之，则不能.想一想 例2：若三角形的两边长分别是2和7，第三边长为奇数，求第三边的长。做一做 设第三边的长为x，根据两边之和大于第三边得：x＜2+7即x＜9根据两边之差小于第三边得：x>7-2即x>5所以x的值大于5小于9，又因为它是奇数，所以x只能取7。解： 等腰三角形一边长９cm，另一边长４cm，它的第三边长是多少？为什么？想一想9cm三角形任意两边之和大于第三边 1.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度,要钉成一个三角形木架,应在下列四根木棒中选取()A.10cm的木棒B.20cm的木棒C.50cm的木棒D.60cm的木棒一、选择题：B练一练 2.已知等腰三角形的两边长分别为3和6,则它的周长为()A.9B.12C.15D.12或153.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为()A.2cmB.3cmC.4cmD.5cmCB练一练x+x+1+x+2=12 4.若五条线段的长分别是1cm,2cm,3cm,4cm,5cm,则以其中三条线段为边可构成______个三角形。二、填空题：5.若等腰三角形的两边长分别为3和7,则它的周长为_______;若等腰三角形的两边长分别是3和4,则它的周长为。6.如果以5cm为等腰三角形的一边,另一边为10cm,则它的周长为________。31710或1125cm 注意等腰三角形在考虑哪条边为腰长时，既要注意有两种情况，还要考虑三角形三边间的关系。 (A)2a-2b(B)2a+2b+2c(C)2b-2c(D)2a-2c（）拓展训练 分析：a+b-c可以看作（a+b）-c,b-a-c则可以看作b-（a+c）由三角形任意两边和大于第三边可得：a+b>c,b0,b-a-c<0而由去绝对值法则：正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0. 原式=（a+b-c）+（b-a-c）=a+b-c+b-a-c=2b-2c我们可以得到： (A)2a-2b(B)2a+2b+2c(C)2b-2c(D)2a-2c（）拓展训练C 某地有四个汽车停车场，位于如图所示的四边形ABCD的四个顶点，现在要建立一个汽车维修站，你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一点P，使点P到A，B，C，D四点的距离之和最小吗？ABCD拓展训练 ABCDP拓展训练AC、BD的交点P就是我们所求的点点P到A，B，C，D四点的距离之和就是AC+BD思考：一定是点P吗？ ABCDPP1拓展训练任意做一点P1，并与A、B、C、D连接则P1到A、B、C、D四点的距离之和为P1A+P1B+P1C+P1D ABCDPP1拓展训练在三角形P1AC中，P1A+P1C>AC在三角形P1BD中，P1B+P1D>BD因此我们得到P1A+P1C+P1B+P1D>AC+BD所以点P即为我们所求点 通过本节课的学习你有哪些收获？课堂小结