七年级下册数学课件《平行线的特征 平行线的特征探究》 (1)_北师大版 30页

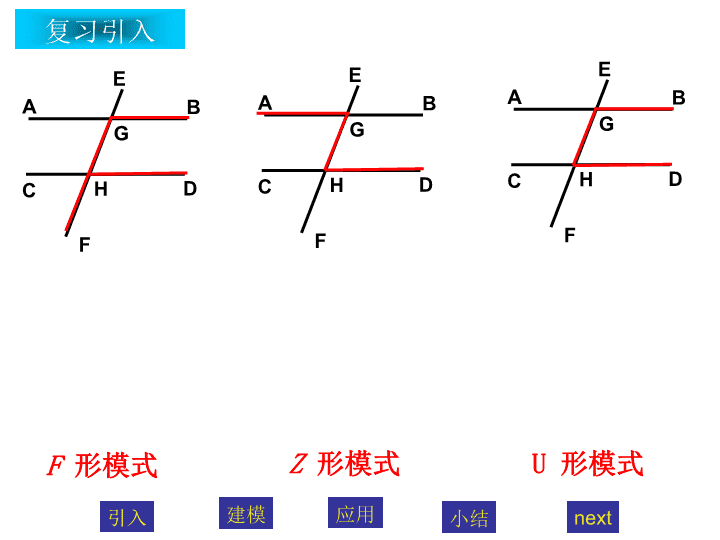
平行线的判定与性质(习题课) 复习引入引入建模应用小结nextABCDEFHGABCDEFHGABCDEFHGF形模式Z形模式U形模式 感悟模式ABCDE∵DE∥BC∴∠B＝∠ADE∴∠C＝∠AED∴∠B＋∠BDE＝180°∴∠C＋∠CED＝180°∴DE∥BC∵∠B＝∠ADE∵∠C＝∠AED∵∠B＋∠BDE＝180°∵∠C＋∠CED＝180°名称:A字形模式建模应用小结next引入 探索模式ABCDE名称:A字形模式∵∠B＝∠ADE∴DE∥BC∴∠C＝∠AED∠B＋∠BDE＝180°∠C＋∠CED＝180°角的关系直线平行判定确定其它角的关系性质结论建模应用小结next引入 感悟模式ABCDO∵AB∥CD∴∠B＝∠D∴∠C＝∠A∵∠B＝∠D∵∠C＝∠A∴DE∥BC名称:8字形模式建模应用小结next引入 探索模式ABCDO名称:8字形模式∵∠B＝∠D∴AB∥CD∴∠C＝∠A角的关系直线平行判定确定其它角的关系性质结论建模应用小结next引入 随堂练习（应用模式）1、填空：（1）∵∠1＝∠B（已知）∴∥（）（2）∵∠2＝∠3（已知）∴∥（）∴∠B＝() 应用模式2、　如图,若AB∥DF,∠2＝∠A,试确定DE与AC的位置关系,并说明理由.ABCDEF2ABCDFACDEF2建模应用小结next引入 应用模式3、　已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有()个.A.2B.3C.4D.5ABCDEFOD建模应用小结next引入 应用模式4、①已知:∠1＝∠2,∠C＝∠D,求证:DF∥AC②已知:∠A＝∠F,∠C＝∠D,求证:DB∥ECABCDEF12建模应用小结next引入 5、已知：CD∥EF,∠1=∠2,求证：∠AGD=∠ACB。证明：∵CD∥EF()(3(2)已知：CD∥EF,∠AGD=∠ACB.求证：∠1=∠2(3)已知：∠AGD=∠ACB∠1=∠2.求证：CD∥EF.∴∠AGD=∠ACB()∴DG∥BC()∴∠1=∠3()∵∠1=∠2()∴∠2=∠3()GA(C)2EBDF1 6、如图，AB∥CD，∠1=∠2，∠E=37°，求：∠F。 7、已知：AB∥CD，MG、NH分别平分∠EMB和∠DNM，那么MG与NH的关系怎样？F12))))ABDEGHNMC43 8、已知：AB∥CD，MG、NH分别平分∠NMB和∠CNM，那么，MG与NH的关系怎样？MFEBDGN1432AHC）（（（ F）1ABCDE）1）2（（21EDCBA）2问：如右图所示，若AB∥CD，则∠AEC与∠A、∠C的关系如何？9:问题探究已知：AB∥CD，求：∠A+∠C+∠AEC=?解：过E点作EF∥AB，则∠A+∠1=180°，∵AB∥CD（）∴EF∥CD（平行于同一直线的两直线互相平行）∴∠2+∠C=180°（）∴∠A+∠1+∠2+∠C=360°（）即∠A+∠C+∠AEC=360°（）ABCDE 探究2、如图甲：已知AB∥DE,那么∠1+∠2+∠3等于多少度？试加以说明。当已知条件不变，而图形变为如图乙时，结论改变了吗？图丙中的∠1+∠2+∠3+∠4是多少度呢？如果如丁图所示，∠1+∠2+∠3+…+∠n的和又为多少度？你找到了什么规律吗？32143213113224n 课堂小结：1、通过习题你有何收获？要判定两条直线平行，可以运用哪些公理或定理？要判定两个角相等或互补，可以运用哪些公理或定理？2、思想方法：分析问题的方法：由已知看可知，扩大已知面。由未知想需知，明确解题方向识图的方法：在定理图形中提炼基本图形，在解题时把复杂图形分解为基本图形平行线习题课 问题1、如图，当∠1=∠2时，AB与CD平行吗？为什么？平行线习题课分析和处理（1）由已知条件∠1=∠2，你可以得到什么？（2）结合图形，你可以得到什么？（3）要说明AB∥CD，只需要满足什么条件？ 2D3()4CAB(1)问题2已知:∠1=∠2试说明:∠3+∠4=180° 结束寄语严格性之于数学家,犹如道德之于人.由“因”导“果”,言必有据.是初学证明者谨记和遵循的原则.下课了!再见平行线习题课 重要做到“五会”(1)会表达：能正确地叙述概念的定义。(2)会识图：能在较复杂的图形中识别出概念所反映的部分。(3)会翻译：能结合图形把概念的定义翻译成符号语言。(4)会画图：能画出概念所反映的几何图形，以及变式图形，会在图上标注字母或符号。(5)会应用：能应用概念进行简单的判断、推理和计算。平行线习题课 课堂练习6、已知：如图∠1=∠2，∠3=∠4，∠5=∠6，求证：EC∥FB 感谢各位领导、专家的莅临指导！敬请批评指正！ 应用模式ABCDEF1231ABCDEABCDF3CDEF2A形模式Z形模式A形模式建模应用小结next引入 应用模式如图,图中包含哪些基本模式?ABCDEFOABDEOBCDFOBDEFOABCD建模应用小结next引入 1、判定两条直线平行有哪些方法？在这些方法中，已经知道了什么？得到的结果是什么？图形已知结论定理同位角内错角同旁内角a//ba//ba//b同位角相等两直线平行内错角相等两直线平行同旁内角互补两直线平行122324））））））abababccc平行线的判定 图形已知结论定理同位角内错角同旁内角a//ba//b内错角相等两直线平行同旁内角互补两直线平行122324））））））abababccc2、已知两条直线平行，同位角，内错角，同旁内角有什么关系？a//b同位角相等两直线平行a//b同位角相等两直线平行a//b同位角相等两直线平行两直线平行同位角相等同旁内角互补两直线平行平行线的性质∠2=∠3a//b同位角相等两直线平行两直线平行内错角相等 课堂练习3已知：AB//DE，∠1=∠2求证：AC//DF）） 问题3、已知：如图，1=2=B，EF∥AB。问：3和C有什么数量关系？为什么？平行线习题课3=C理由：∵1=B（）∴DE∥BC（）∴2=C（）∵EF∥AB（）∴B=3（）又∵2=B（）∴3=C（） 课堂练习4、如图，已知BF平分∠ABC，∠CEB=∠CBE，∠A=∠C求证：BC∥AF平行线习题课