七年级下数学课件《互逆命题》 (18)_苏科版 23页

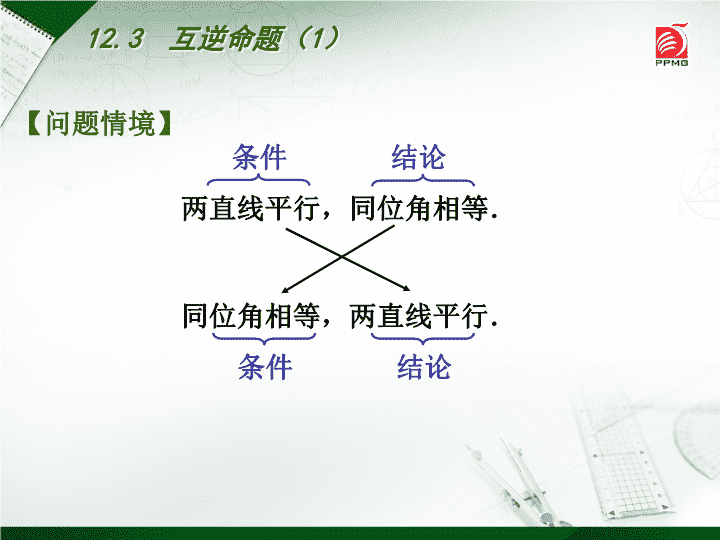
12.3互逆命题（1）七年级(下册)初中数学 命题有真有假。正确的命题是真命题，错误的命题是假命题回顾什么是命题?一般地，对某一件事情作出判断的句子叫做命题。命题可看做由条件和结论两部分组成。命题由哪两部分组成? 12.3互逆命题（1）两直线平行，同位角相等．条件结论同位角相等，两直线平行．条件结论【问题情境】 12.3互逆命题（1）如果a＋b＞0，那么a＞0，b＞0如果a＞0，b＞0，那么a＋b＞0【问题情境】条件结论条件结论 12.3互逆命题（1）两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题.其中一个命题是另一个命题的逆命题. 1.下列这些命题中，哪些是互逆命题？①直角都相等；②内错角相等，两直线平行；③如果a+b>0,那么a>0,b>0；④相等的角都是直角；⑤如果a>0,b>0,那么ab>0；⑥两直线平行，内错角相等。辨析 1.下列这些命题中，哪些是互逆命题？①直角都相等；②内错角相等，两直线平行；③如果a+b>0,那么a>0,b>0；④相等的角都是直角；⑤如果a>0,b>0,那么ab>0；⑥两直线平行，内错角相等。辨析 1.下列这些命题中，哪些是互逆命题？①直角都相等；②内错角相等，两直线平行；③如果a+b>0,那么a>0,b>0；④相等的角都是直角；⑤如果a>0,b>0,那么ab>0；⑥两直线平行，内错角相等。辨析 1.下列这些命题中，哪些是互逆命题？③如果a+b>0,那么a>0,b>0；⑤如果a>0,b>0,那么ab>0。辨析如果a>0,b>0,那么a+b>0；如果ab>0,那么a>0,b>0。 把一个命题的条件和结论互换就得到它的逆命题，所以每个命题都有逆命题。心得 1．下列各组命题是否是互逆命题：（1）“正方形的四个角都是直角”与“四个角都是直角的四边形是正方形”；（2）“等于同一个角的两个角相等”与“如果两个角都等于同一个角，那么这两个角相等”；（3）“对顶角相等”与“如果两个角相等，那么这两个角是对顶角”；（4）“同位角相等，两直线平行”与“同位角不相等，两直线不平行”．12.3互逆命题（1）【试一试】 2．说出下列命题的逆命题，并与同学交流．（1）如果a2＝b2，那么a＝b；（2）如果两个角是对顶角，那么它们的平分线组成一个平角；（3）末位数字是5的数，能被5整除；（4）锐角与钝角互为补角.12.3互逆命题（1）【试一试】逆命题：如果a＝b，那么a2＝b2.逆命题：如果两个角的平分线组成一个平角，那么这两个角是对顶角.逆命题：能被5整除的数的末位数字是5．逆命题：互为补角的两个角一个是锐角一个是钝角． 下列的命题正确吗？为什么？（1）如果a＞0，那么a2＞0（2）锐角与钝角互为补角正确不正确300的锐角与1000的钝角不互为补角小结1.判断一个命题是假命题，只需举___________.2.如果一个命题是真命题，它的逆命题__________是真命题.像这样，举出一个例子来说明一个命题是假命题，这样的例子称为反例。反例不一定 举反例说明下列命题是假命题：（1）如果|a|＝|b|，那么a＝b；（2）任何数的平方大于0；（3）两个锐角的和是钝角；（4）如果一点到线段两端的距离相等，那么这点是这条线段的中点．12.3互逆命题（1）【练一练】 检测与练习1.“两直线平行，内错角相等”的逆命题是____________________________.2.命题“对顶角相等”的逆命题是______________________，这个逆命题是____命题.3.请写出一个原命题是真命题，逆命题是假命题的命题：____________________________________________内错角相等，两直线平行.相等的角是对顶角假等腰三角形是轴对称图形。 4.写出下列命题的逆命题，并判断原命题与逆命题的真假.(1)如果|a|=|b|，那么a=b；(2)如果a＞0，那么a2＞0；(3)等角的补角相等；(4)同旁内角互补，两直线平行.假命题如果a=b，那么|a|=|b|；真命题真命题如果a2＞0，那么a＞0；假命题真命题如果两个角的补角相等，那么这两个角相等。真命题真命题两直线平行，同旁内角互补.真命题www.xkb1.com 5.举反例说明下列命题是假命题.(1)如果a+b＞0，那么a＞0，b＞0;(2)同位角一定相等.(3)两个锐角的和是锐角a=10，b=-2)1)2100，850www.xkb1.com 应用4.如图，现有以下三个论断：①b⊥c，②a⊥c，③a∥b。请以其中任意两个论断为条件，第三个论断为结论构造一个命题，并写出这个命题的逆命题。abc判断你所构造的命题是真命题还是假命题？ 第一次数学危机公元前五世纪，毕达哥拉斯学派认为“万物皆是数”——任何数都可以表示为整数或整数的比.他的门徒希伯索斯发现一个反例：当正方形边长为整数1时，对角线的长就无法用整数表示！从而引发第一次数学危机.希伯索斯因为没有按毕达哥拉斯“保持沉默”的要求，把这个问题公之于众，结果被投尸大海，葬身鱼腹，造成历史上震惊数学界的无理数发现惨案.12.3互逆命题（1）【拓展延伸】 12.3互逆命题（1）著名的反例公元1640年，法国著名数学家费尔马发现：220＋1＝3，221＋1＝5，222＋1＝17，223＋1＝257，224＋1＝65537……而3、5、17、257、65537都是质数，于是费尔马猜想：对于一切自然数n，22n＋1都是质数，可是，到了1732年，数学家欧拉发现：225＋1＝4294967297＝641×6700417.这说明了22n＋1是一个合数，从而否定了费尔马的猜想.【拓展延伸】 【小结】本节课你学会了什么？你有什么收获？12.3互逆命题（1） 课本P161习题12.3第1、2题.7.1探索直线平行的条件（1）【课后作业】 谢谢!