北师大版数学七年级上册《角的比较》练习 4页

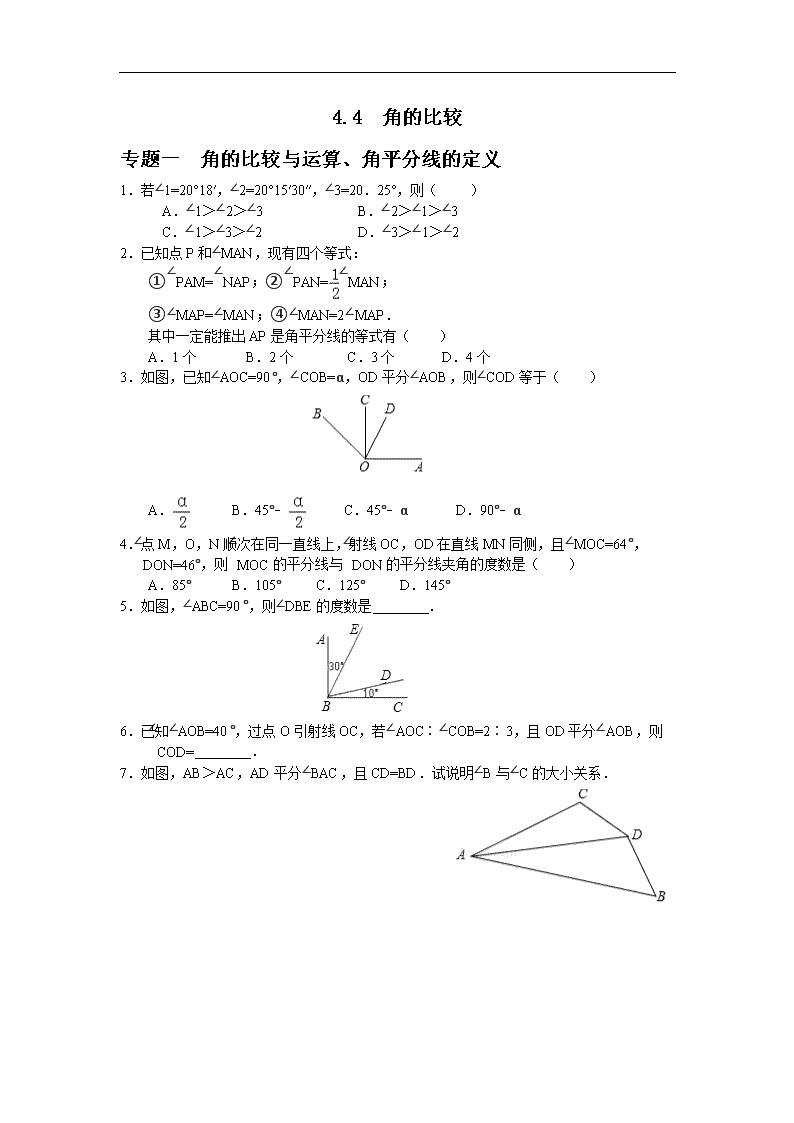
4.4 角的比较 专题一 角的比较与运算、角平分线的定义 1．若∠1=20°18′，∠2=20°15′30′′，∠3=20．25°，则（ ） A．∠1＞∠2＞∠3 B．∠2＞∠1＞∠3 C．∠1＞∠3＞∠2 D．∠3＞∠1＞∠2 2．已知点 P 和∠MAN，现有四个等式： ①∠PAM=∠NAP；②∠PAN= ∠MAN； ③∠MAP=∠MAN；④∠MAN=2∠MAP． 其中一定能推出 AP 是角平分线的等式有（ ） A．1 个 B．2 个 C．3 个 D．4 个 3．如图，已知∠AOC=90°，∠COB=α，OD 平分∠AOB，则∠COD 等于（ ） A． B．45°﹣ C．45°﹣α D．90°﹣α 4．点 M，O，N 顺次在同一直线上，射线 OC，OD 在直线 MN 同侧，且∠MOC=64°，∠DON=46°， 则∠MOC 的平分线与∠DON 的平分线夹角的度数是（ ） A．85° B．105° C．125° D．145° 5．如图，∠ABC=90°，则∠DBE 的度数是 ． 6．已知∠AOB=40°，过点 O 引射线 OC，若∠AOC∶∠COB=2∶3，且 OD 平分∠AOB， 则∠COD= ． 7．如图，AB＞AC，AD 平分∠BAC，且 CD=BD．试说明∠B 与∠C 的大小关系． 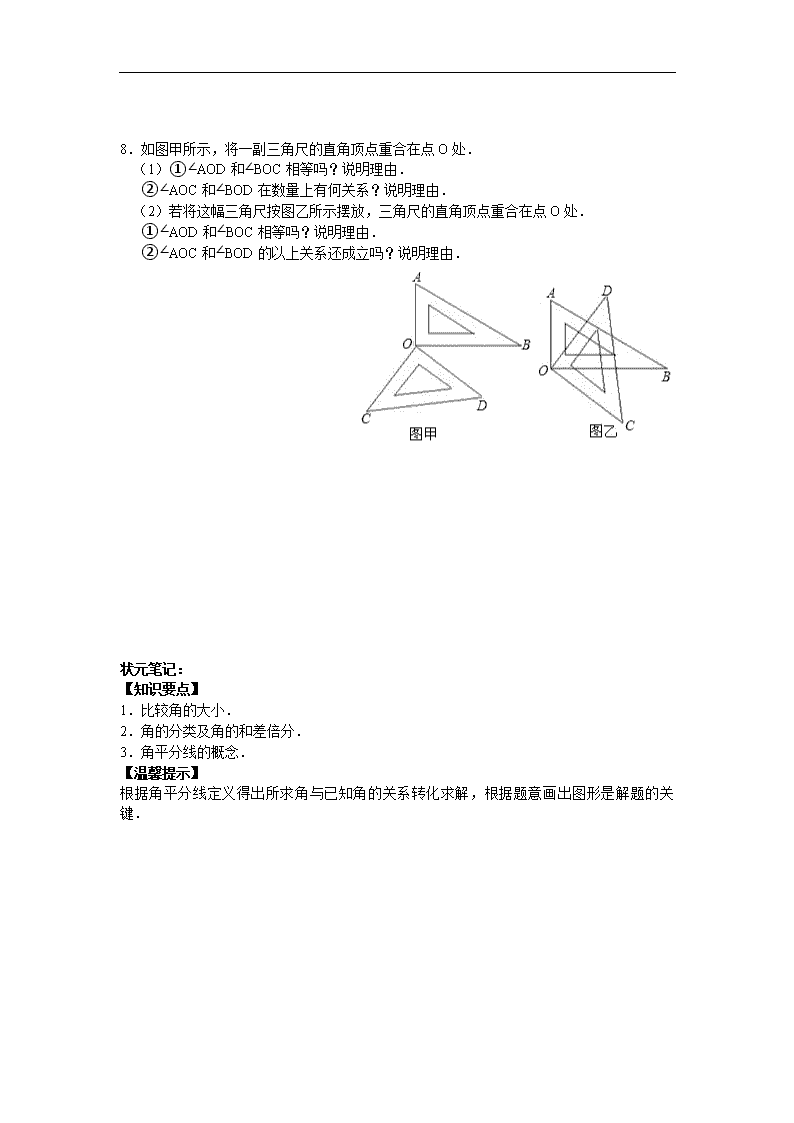8．如图甲所示，将一副三角尺的直角顶点重合在点 O 处． （1）①∠AOD 和∠BOC 相等吗？说明理由． ②∠AOC 和∠BOD 在数量上有何关系？说明理由． （2）若将这幅三角尺按图乙所示摆放，三角尺的直角顶点重合在点 O 处． ①∠AOD 和∠BOC 相等吗？说明理由． ②∠AOC 和∠BOD 的以上关系还成立吗？说明理由． 状元笔记： 【知识要点】 1．比较角的大小． 2．角的分类及角的和差倍分． 3．角平分线的概念． 【温馨提示】 根据角平分线定义得出所求角与已知角的关系转化求解，根据题意画出图形是解题的关键． 参考答案： 1．A 2．A 3．B 解析：∵∠AOC=90°，∠COB=α，∴∠AOB=90°+α． ∵OD 平分∠AOB，∴∠AOD= ∠AOB= （90°+α）=45°+ ， ∠COD=∠AOC﹣∠AOD=90°﹣（45°+ ）=45°﹣ ． 4．C 解析：如图，设∠MOC 的平分线为 OE，∠DON 的平分线为 OF，∵∠MOC=64°， ∠DON=46°，∴∠MOE= ∠MOC= ×64°=32°，∠NOF= ∠DON= ×46°=23°， ∴∠EOF=180°﹣∠MOE﹣∠NOF=180°﹣32°﹣23°=125°． 5． 50° 解析：根据图形，易得∠DBE=∠ABC﹣∠ABE﹣∠COD=90°﹣30°﹣10°=50°． 6． 4°或 100° 解析：如图（1），射线 OC 在∠AOB 的内部，图（2）射线 OC 在∠AOB 的 外部． （1）设∠AOC、∠COB 的度数分别为 2x、3x，则 2x+3x=40°，∴x=8°，∠AOC=2x=16°， ∠AOD= ×40°=20°，∴∠COD=∠AOD﹣∠AOC=20°﹣16°=4°． （2）设∠AOC、∠COB 的度数分别为 2x、3x，则∠AOB=3x﹣2x=x=40°， ∴∠AOC=2x=80°，∠AOD=20°，∴∠COD=∠AOC+∠AOD=80°+20°=100°． 7．解：由题意知，∠C=180°﹣∠CAD﹣∠CDA，∠B=180°﹣∠DAB﹣∠ADB， ∵AB＞AC，AD 平分∠BAC，且 CD=BD， ∴∠CAD=∠BAD，∠CDB＜∠ADB，∴∠C＞∠B． 8．解：（1）①相等．理由： ∵∠AOD=90°+∠BOD，∠BOC=90°+∠BOD，∴∠AOD 和∠BOC 相等． ②∠AOC+∠BOD=180°．理由： ∵∠AOC+90°+∠BOD+90°=360°，∴∠AOC+∠BOD=180°； （2）①相等．理由：∵∠AOD=90°﹣∠BOD，∠BOC=90°﹣∠BOD，∴∠AOD 和∠BOC 相等． ②成立．理由：∵∠AOC=90°+90°﹣∠BOD，∴∠A OC+∠BOD=180°．