浙教版数学七年级下册第1章《平行线》单元测试 8页

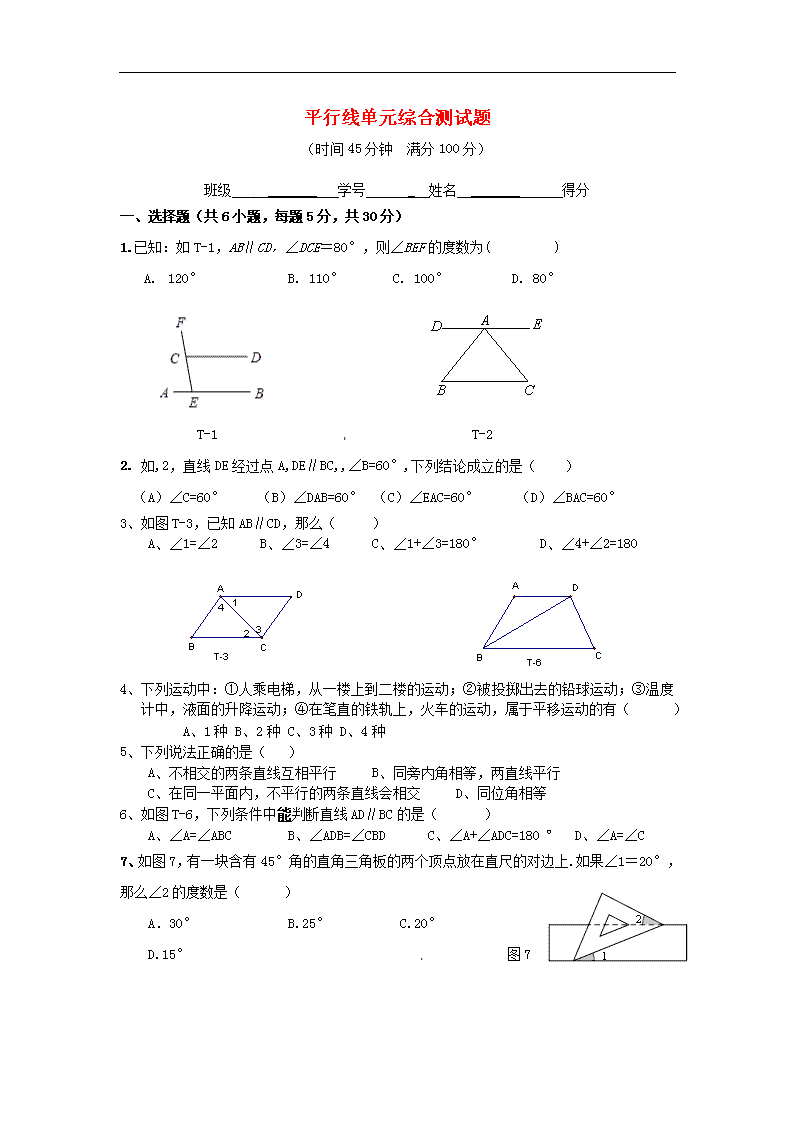
平行线单元综合测试题 （时间 45 分钟 满分 100 分） 班级 _______ 学号 _ 姓名 _______ 得分 一、选择题（共 6 小题，每题 5 分，共 30 分） 1.已知：如 T-1，AB∥CD，∠DCE＝80°，则∠BEF 的度数为( ) A. 120° B. 110° C. 100° D. 80° E D C B A T-1 T-2 2. 如,2，直线 DE 经过点 A,DE∥BC,,∠B=60°,下列结论成立的是（ ） （A）∠C=60° （B）∠DAB=60° （C）∠EAC=60° （D）∠BAC=60° 3、如图 T-3，已知 AB∥CD，那么（ ） A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠4+∠2=180 4、下列运动中：①人乘电梯，从一楼上到二楼的运动；②被投掷出去的铅球运动；③温度 计中，液面的升降运动；④在笔直的铁轨上，火车的运动，属于平移运动的有（ ） A、1 种 B、2 种 C、3 种 D、4 种 5、下列说法正确的是（ ） A、不相交的两条直线互相平行 B、同旁内角相等，两直线平行 C、在同一平面内，不平行的两条直线会相交 D、同位角相等 6、如图 T-6，下列条件中能判断直线 AD∥BC 的是（ ） A、∠A=∠ABC B、∠ADB=∠CBD C、∠A+∠ADC=180 º D、∠A=∠C 7、如图 7，有一块含有 45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1＝20°， 那么∠2 的度数是（ ） A．30° B.25° C.20° D.15° 图 7 A B C D 1 2 4 3 T-3 T-6 A B C D 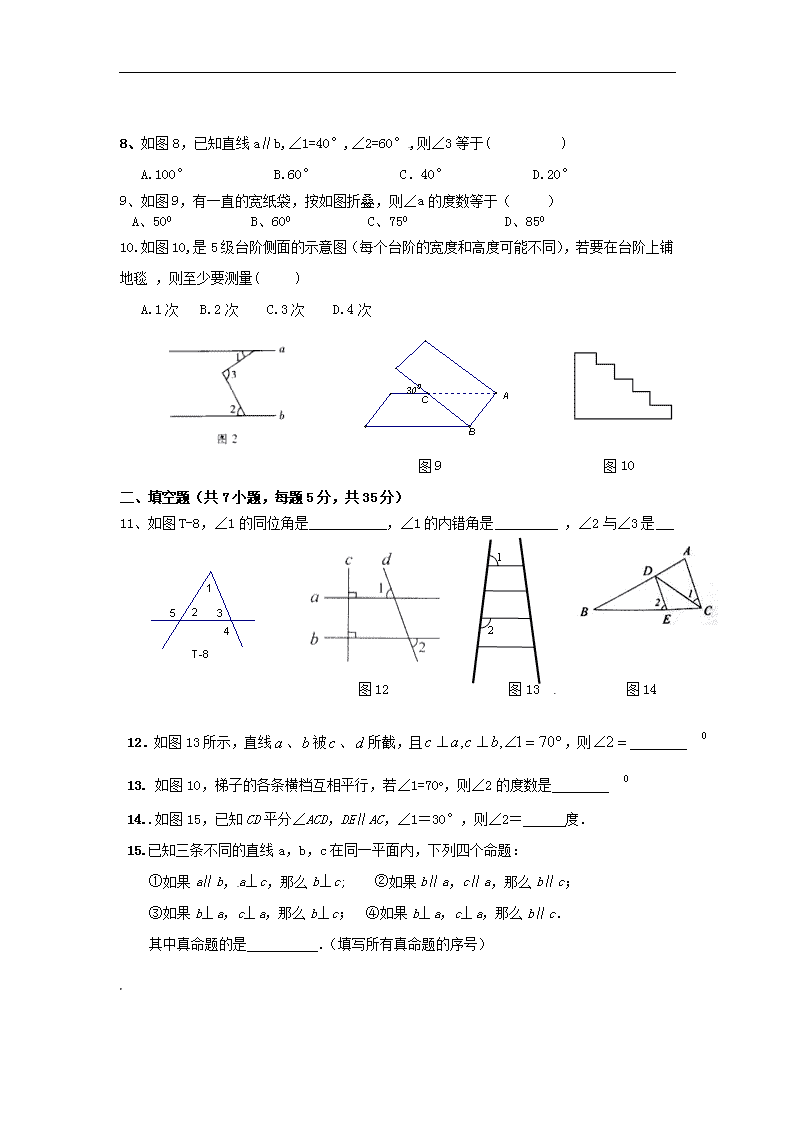8、如图 8，已知直线 a∥b,∠1=40°,∠2=60° ,则∠3 等于( ) A.100° B.60° C．40° D.20° 9、如图 9，有一直的宽纸袋，按如图折叠，则∠a 的度数等于（ ） A、500 B、600 C、750 D、850 10. 如图 10,是 5 级台阶侧面的示意图（每个台阶的宽度和高度可能不同），若要在台阶上 铺地毯 ，则至少要测量( ) A.1 次 B.2 次 C.3 次 D.4 次 图 9 图 10 二、填空题（共 7 小题，每题 5 分，共 35 分） 11、如图 T-8，∠1 的同位角是 ，∠1 的内错角是 ，∠2 与∠3 是 图 12 图 13 图 14 12．如图 13 所示，直线 a 、b 被 c 、d 所截，且  701,, bcac ，则 2 0 13. 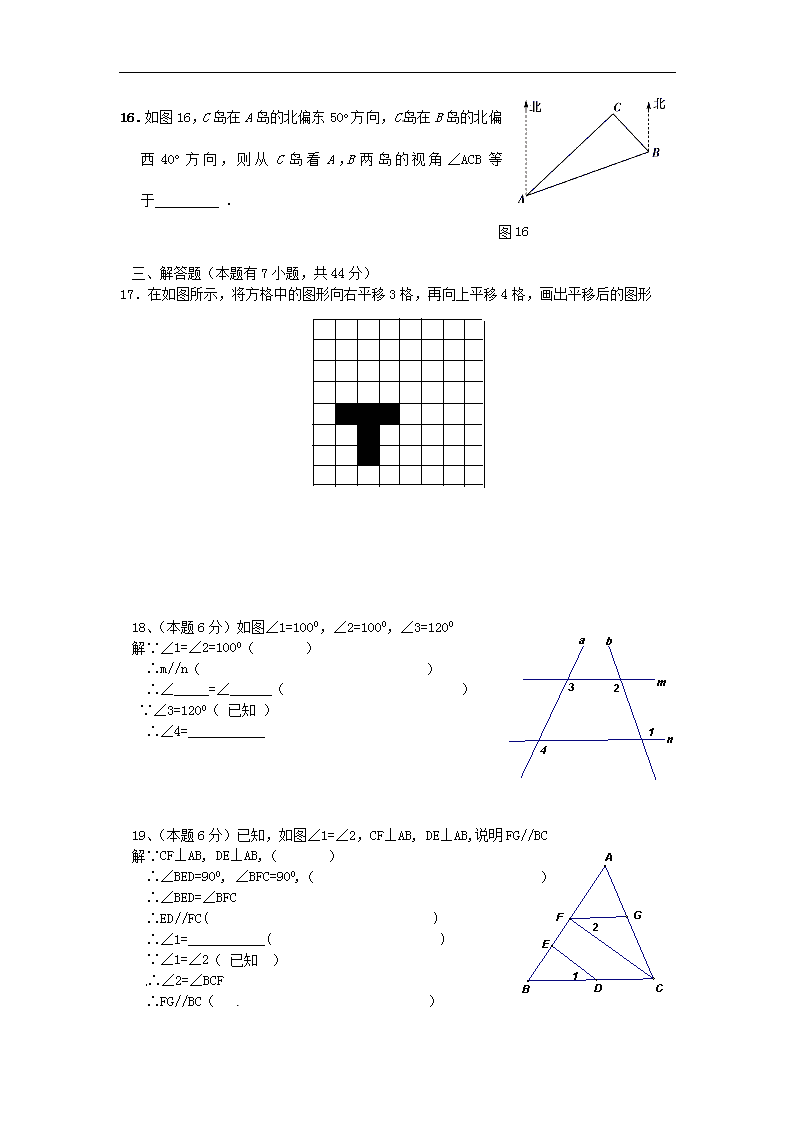如图 10，梯子的各条横档互相平行，若∠1=70o，则∠2 的度数是 0 14..如图 15，已知 CD 平分∠ACD，DE∥AC，∠1＝30°，则∠2＝ 度． 15.已知三条不同的直线 a，b，c 在同一平面内，下列四个命题： ①如果 a∥b，a⊥c，那么 b⊥c; ②如果 b∥a，c∥a，那么 b∥c； ③如果 b⊥a，c⊥a，那么 b⊥c； ④如果 b⊥a，c⊥a，那么 b∥c． 其中真命题的是 ．（填写所有真命题的序号） 30 0 C B A T-8 1 2 4 3 5 16．如图 16，C 岛在 A 岛的北偏东 50o 方向，C岛在 B 岛的北偏 西 40o 方 向 ， 则 从 C 岛 看 A ， B 两 岛 的 视 角 ∠ACB 等 于 ． 图 16 三、解答题（本题有 7 小题，共 44 分） 17．在如图所示，将方格中的图形向右平移 3 格，再向上平移 4 格，画出平移后的图形 18、（本题 6 分）如图∠1=1000，∠2=1000，∠3=1200 解∵∠1=∠2=1000（ ） ∴m//n（ ） ∴∠_____=∠______（ ） ∵∠3=1200（ 已知 ） ∴∠4=___________ 19、（本题 6 分）已知，如图∠1=∠2，CF⊥AB, DE⊥AB,说明 FG//BC 解∵CF⊥AB, DE⊥AB,（ ） ∴∠BED=900, ∠BFC=900, （ ） ∴∠BED=∠BFC ∴ED//FC( ) ∴∠1=___________( ) ∵∠1=∠2（ 已知 ） ∴∠2=∠BCF 4 2 3 1 n m b a 2 1 G F E D C B A ∴FG//BC（ ） 14、如图：已知；AB∥CD，AD∥BC，∠B 与∠D 相等吗？试说明理由． 15、如图，∠1+∠2=180°，∠DAE=∠BCF，DA 平分∠BDF． （1）AE 与 FC 会平行吗?说明理由． （2）AD 与 BC 的位置关系如何?为什么? （3）BC 平分∠DBE 吗?为什么． F E 2 1 D C B A 16、如图，已知直线 l1∥l2，直线 l3 和直线 l1、l2 交于点 C 和 D，在 C、D 之间有一点 P，如 果 P 点在 C、D 之间运动时，问∠PAC，∠APB，∠PBD 之间的关系是否发生变化.若点 P 在 C、D 两点的外侧运动时（P 点与点 C、D 不重合），试探索∠PAC，∠APB，∠PBD 之间 的关系又是如何？ l1 l C B D P l2 A D C BA 参考答案 一、选择题（共 6 小题，每题 5 分，共 30 分） 1. （2011 江苏南通）已知：如图 1，AB∥CD，∠DCE＝80°，则∠BEF 的度数为 B. 120° B. 110° C. 100° D. 80° 【答案】C E D C B A 图 1 图 2 图 3 2.（2011四川南充市）如,2，直线DE经过点A,DE∥BC,,∠B=60°,下列结论成立的是（ ） （A）∠C=60° （B）∠DAB=60° （C）∠EAC=60° （D）∠BAC=60° 【答案】B 3. （2010 湖北孝感）如图 3，直线 AB、CD 相交于点 O，OT⊥AB于 O，CE∥AB 交 CD 于点 C， 若∠ECO=30°，则∠DOT=（ ） A.30° B.45° C. 60° D. 120° 【答案】C 4、（2011 浙江丽水）如图 4，有一块含有 45°角的直角三角板的两个顶点放在直尺的对边 上.如果∠1＝20°，那么∠2 的度数是（ ） A．30° B.25° C.20° D.15° 【答案】B 图 4 图 5 图 6 5、（2011 广东株洲，）某商品的商标可以抽象为如图 5 所示的三条线段，其中 AB∥CD，∠ EAB=45°，则∠FDC 的度数是( ) 图 10 A．30 B． 45 C． 60 D． 75 【答案】B 6、（2011 湖南怀化）如图 6，已知直线 a∥b,∠1=40°,∠2=60°,则∠3 等于 A.100° B.60° C．40° D.20° 【答案】A 二、填空题（共 7 小题，每题 5 分，共 35 分） 7．（2010 浙江衢州）如图 7，直线 DE 交∠ABC 的边 BA 于点 D，若 DE∥BC，∠B=70°， 则∠ADE 的度数是 ． 【答案】70° 1 2 3 4 5A B C D E F 图 7 图 8 图 9 8．（2010 广西桂林）如图 8，直线 AB、CD 被直线 EF 所截，则∠3 的同旁内角是（ ）． A．∠1 B．∠2 C．∠4 D．∠5 【答案】B 9．（2010 广西南宁）如图 9 所示，直线 a 、b 被 c 、 d 所截，且  701,, bcac ， 则 2 0 【答案】70 10．（2010 广东茂名）如图 10，梯子的各条横档互相平行，若∠1=70o，则∠2 的度数是 A．80o B．110o C．120o D．140o 图 11 图 12 【答案】B 11. （2011 广东广州市）已知三条不同的直线 a，b，c 在同一平面内，下列四个命题： ①如果 a∥b，a⊥c，那么 b⊥c; ②如果 b∥a，c∥a，那么 b∥c； C A ED B ③如果 b⊥a，c⊥a，那么 b⊥c； ④如果 b⊥a，c⊥a，那么 b∥c． 其中真命题的是 ．（填写所有真命题的序号） 【答案】①②④ 12. (2011 浙江湖州).如图 11，已知 CD 平分∠ACD，DE∥AC，∠1＝30°，则∠2＝ 度． 【答案】60 13．（2010 山东日照）如图 12，C 岛在 A 岛的北偏东 50o 方向，C 岛在 B 岛的北偏西 40o 方向， 则从 C 岛看 A，B 两岛的视角∠ACB 等于 ． 【答案】90o 三、解答题（共 25 分） 14、如图：已知；AB∥CD，AD∥BC，∠B 与∠D 相等吗？试说明理由． 【答案】相等。理由略。 15、如图，∠1+∠2=180°，∠DAE=∠BCF，DA 平分∠BDF． （1）AE 与 FC 会平行吗?说明理由． （2）AD 与 BC 的位置关系如何?为什么? （3）BC 平分∠DBE 吗?为什么． F E 2 1 D C B A 【答案】（1）平行；（2）平行； （3） 平分。理由略。 16、如图，已知直线 l1∥l2，直线 l3 和直线 l1、l2 交于点 C 和 D，在 C、D 之间有一点 P，如 果 P 点在 C、D 之间运动时，问∠PAC，∠APB，∠PBD 之间的关系是否发生变化.若点 P D C BA 在 C、D 两点的外侧运动时（P 点与点 C、D 不重合），试探索∠PAC，∠APB，∠PBD 之间 的关系又是如何？ 解： 若 P 点在 C、D 之间运动时，则有∠APB＝∠PAC+∠PBD. 理由是：如图 4，过点 P 作 PE∥l1，则∠APE＝∠PAC， 又因为 l1∥l2，所以 PE∥l2，所以∠BPE＝∠PBD， 所以∠APE+∠BPE＝∠PAC+∠PBD，即∠APB＝∠PAC+∠PBD. 若点 P 在 C、D 两点的外侧运动时（P 点与点 C、D 不重合），则有两种情形： （1）如图 1，有结论：∠APB＝∠PBD－∠PAC. 理由是：过点 P 作 PE∥l1，则∠APE＝∠PAC， 又因为 l1∥l2，所以 PE∥l2，所以∠BPE＝∠PBD， 所以∠APB＝∠BAE+∠APE，即∠APB＝∠PBD－∠PAC. （2）如图 2，有结论：∠APB＝∠PAC－∠PBD. 理由是：过点 P 作 PE∥l2，则∠BPE＝∠PBD， 又因为 l1∥l2，所以 PE∥l1，所以∠APE＝∠PAC， 所以∠APB＝∠APE+∠BPE，即∠APB＝∠PAC+∠PBD. l1 l C B D P l2 A E 图 1 C Dl2 P l3 l1 A B E 图 2 C D l2 P l3 l1 A B