华师版 七年级数学下册-周周清7检测试卷10-3-10-5 4页

检测内容：10.3－10.5 得分________卷后分________评价________ 一、选择题(每小题 4 分，共 24 分) 1．(泸州中考)下列正多边形中，不是中心对称图形的是( B ) A B C D 2．(天水中考)下列图形中，是中心对称图形但不是轴对称图形的是( C ) A B C D 3．如图，四边形 ABCD 为正方形，O 为对角线 AC，BD 的交点，则△COD 绕点 O 经过 下列哪种旋转可以得到△DOA( C ) A．顺时针旋转 90°B．顺时针旋转 45° C．逆时针旋转 90°D．逆时针旋转 45° 第 3 题图 第 4 题图 4．如图，点 O 为同心圆的圆心，线段 AB＝4cm，且 CD⊥AB 于点 O，则阴影部分的面 积是( B ) A．2πcm2B．πcm2C．π 2 cm2D．4πcm2 5．下面各图形中，不能通过所给图形旋转得到的是( D ) A B C D 第 5 题图 第 6 题图 6．如图，将正五边形 ABCDE 的点 C 固定，并按顺时针方向旋转，要使新五边形 A′B′CD′E′ 的顶点 D′落在直线 BC 上，则旋转角度为( B ) A．108°B．72°C．54°D．36° 二、填空题(每小题 4 分，共 16 分) 7．如图，下列各组图形中，由左边变成右边的图形，分别进行了平移，旋转，轴对称， 中心对称等变换，其中进行平移变化的是__③__，进行旋转变换的是__①④__，进行轴对称 变换的是__②__，进行中心对称变换的是__④__.(填序号) 8．如图，将△ABC 沿直线 DE 折叠后，使得点 B 与点 A 重合．已知 AC＝5cm，△ADC 的周长为 17cm，则 BC 的长为__12___cm. 第 8 题图 第 9 题图 9．如图，是一个 3×3 的正方形网格，则∠1＋∠2＋∠3＋∠4＝__180°__． 10．如图，AB∥CD，直线 l 与 AB，CD 分别相交于点 F，E，将直线 l 绕点 E 逆时针旋 转 40°后，与直线 AB 相交于点 G，若∠GEC＝80°，则∠GFE＝__60__°. 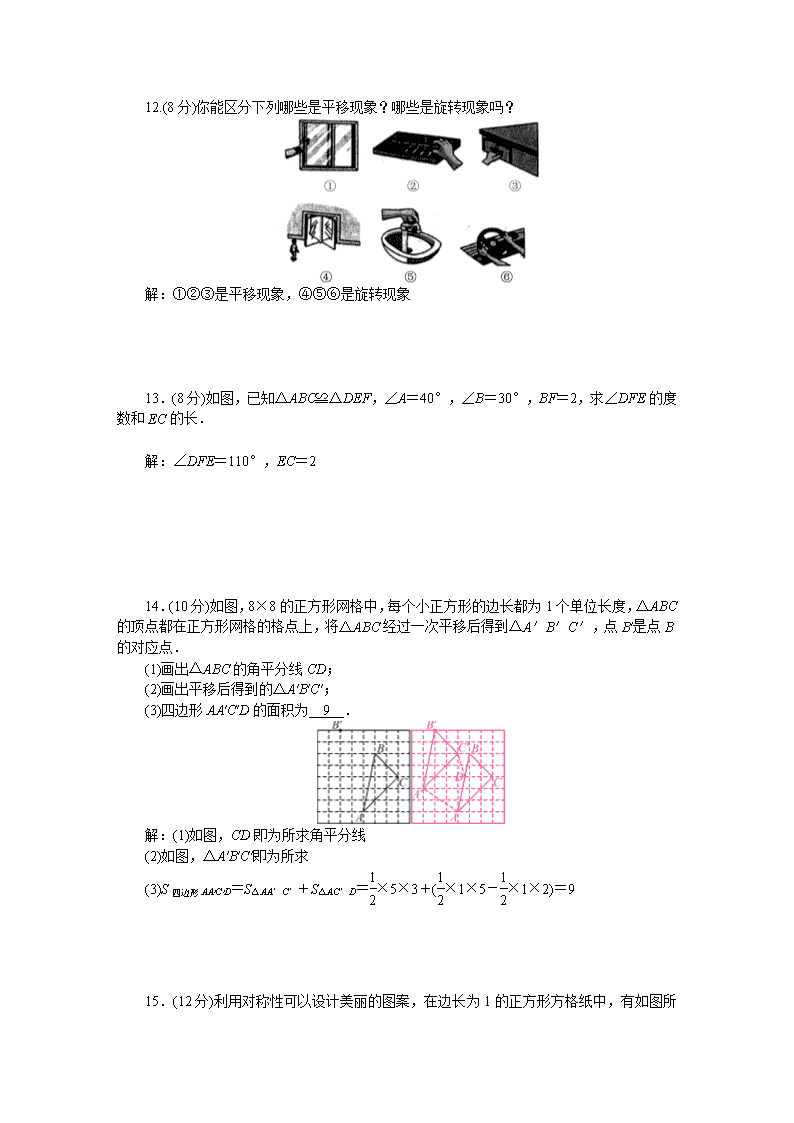三、解答题(共 60 分) 11．(8 分)如图，将 Rt△ABC 绕直角顶点 C 按顺时针方向旋转 38°得到 Rt△A′B′C, 若 AC⊥A′B′，求∠ABC 的度数． 解：∵Rt△ABC 绕直角顶点 C 顺时针方向旋转 38°得到 Rt△A′B′C，∴∠A＝∠A′， ∠ACA′＝38°，∵AC⊥A′B′，∴∠A′＝90°－∠ACA′＝52°＝∠A， 在 Rt△ABC 中，∠B＝90°－∠A＝38° 12.(8 分)你能区分下列哪些是平移现象？哪些是旋转现象吗？ 解：①②③是平移现象，④⑤⑥是旋转现象 13．(8 分)如图，已知△ABC≌△DEF，∠A＝40°，∠B＝30°，BF＝2，求∠DFE 的度 数和 EC 的长． 解：∠DFE＝110°，EC＝2 14．(10 分)如图，8×8 的正方形网格中，每个小正方形的边长都为 1 个单位长度，△ABC 的顶点都在正方形网格的格点上，将△ABC 经过一次平移后得到△A′B′C′，点 B′是点 B 的对应点． (1)画出△ABC 的角平分线 CD； (2)画出平移后得到的△A′B′C′； (3)四边形 AA′C′D 的面积为__9__． 解：(1)如图，CD 即为所求角平分线 (2)如图，△A′B′C′即为所求 (3)S 四边形 AA′C′D＝S△AA′C′＋S△AC′D＝1 2 ×5×3＋(1 2 ×1×5－1 2 ×1×2)＝9 15．(12 分)利用对称性可以设计美丽的图案，在边长为 1 的正方形方格纸中，有如图所 示的四边形(顶点都在格点上). (1)先作出该四边形关于直线 l 成轴对称的图形，再作出上面所作的图形连同原四边形绕 点 O 按顺时针方向旋转 90°后的图形； (2)完成上述设计后，求出整个图案的面积． 解：(1)如图所示 (2)一个四边形面积为：1 2 ×5×1×2＝5， 整个图案面积为：5×4＝20. 16．(14 分)如图所示，正方形网格中，△ABC 为格点三角形(即三角形的顶点都在格点上). (1)把△ABC 沿 BA 方向平移后，点 A 移到点 A1，在网格中画出平移后得到的△A1B1C1； (2)把△A1B1C1 绕点 A1 按逆时针方向旋转 90°，得到△A1B2C2，在网格中画出旋转后的 △A1B2C2； (3)连结 C1C2，请判断△A1C1C2 的形状，并说明理由. 解：(1)如图，△A1B1C1 为所作 (2)如图，△A1B2C2 为所作 (3)△A1C1C2 为等腰直角三角形． 理由如下： ∵△A1B1C1 绕点 A1 按逆时针方向旋转 90°，得到△A1B2C2， ∴A1C1＝A1C2，∠C2A1C1＝90°， ∴△A1C1C2 为等腰直角三角形