2019七年级数学上学期第7次假期作业（无答案） 4页

七年级（上）数学假期作业7‎ 班级：________ 学号______ 姓名：__________家长签字： 得分：__________‎ 一、细心选一选（每题3分，共24分）‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答 案 ‎1、两数和的平方可以表示为 ‎ A． B． C． D．‎ ‎2、下列说法中正确的个数是 ‎ ‎(1) a和0都是单项式. (2)多项式‎-3a2b+‎7a2b2-2ab+1的次数是3. ‎ ‎(3)单项式的系数为－2. (4)x+2xy-y可读作x、2xy、-y的和.‎ A.1个 B.2个 C. 3个 D.4个 ‎3、某种细菌在培养过程中，每半个小时分裂一次（由1个分裂成2个，两个分裂成4个…），若这种细菌由1个分裂成64个，那么这个过程需要经过（ ）小时。‎ A． B． C． D．‎ ‎4、在 ，12，—20， ，，中，负数的个数有 ‎ A.个 B. 个 C. 个 D. 个 ‎5、下列式子：中，整式的个数是: ‎ A. 6 B. ‎5 C. 4 D. 3‎ ‎6、某校阶梯教室第一排有m个座位，后面每排比前一排多2个座位，则第n排的做位数是A．ｍ＋2ｎ B．mn+‎2 C．m+2（n—1） D．m+（n+2）‎ a b c ‎7、按下面的程序计算，若开始输入的值x为正数，最后输出的结果为1339，则满足条件的x的不同值最多有 A．2个 B．3个 C．4个 D．5个 ‎8、火车站、机场、邮局等场所都有为旅客提供打包服务的项目．现有一个长、宽、高分别为、、 的箱子，按如图所示的方式打包，则打包带的长（不计接头处）至少为 ‎ 4‎ ‎ A．‎2a＋2b＋‎4c B．‎2a＋4b＋‎6c C．‎4a＋6b＋‎6c D．‎4a＋4b＋‎‎8c 二、认真填一填（每题2分，计20分）‎ 输入n ‎ 计算的值 ‎>200‎ 输出结果 no ‎ yes ‎ ‎9、单项式的系数是 ,次数是 .‎ ‎10、在数轴上与﹣3相距4个单位长度的点表示的数是　　　　　　‎ ‎11、一个两位数，个位数字是a，十位数字比个位数字大2，‎ 则这个两位数可表示为_______________.‎ ‎12、若|a|=4，|b|=2，且ab<0，则a+b= 。‎ ‎13、如右图，是一个简单的数值运算程序，当输入的值为2时，‎ 则输出的数值为 ‎ ‎14、已知代数式x－2y的值是3，则代数式2x+1－4y值是_______.‎ ‎15、多项式是 次___项式，最高次项系数是 ‎ ‎16、甲乙两班共有x人，若从甲班调a人到乙班后，则甲乙两班人数正好相等。甲班原有人数是______________人.‎ ‎17、甲、乙两地相距x千米，某人原计划5小时到达，后因故提前1小时到达,则实际每小时比原计划多走_________________________千米(用代数式表示) .‎ ‎18、将一张长方形的纸对折，如图所示，可得到一条折痕（图中虚线），继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么如果对折五次，可以得到 条折痕。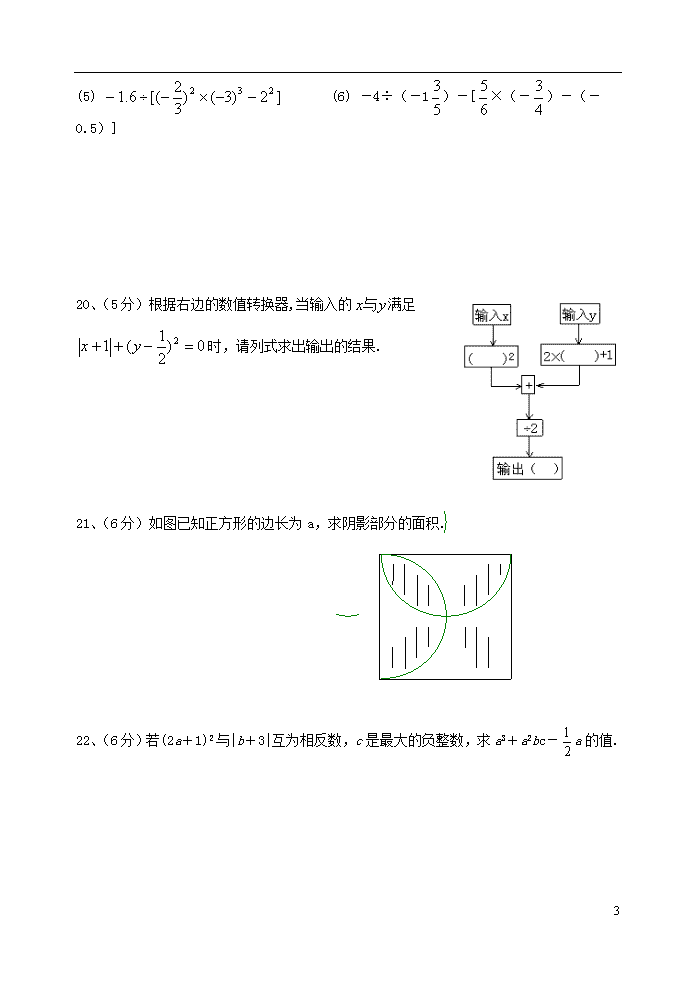‎ 三、解答题（合计46分）‎ ‎19、计算（每小题4分，24分）‎ ‎（1） （2）‎ ‎ ‎ ‎（3）－3.5÷×(－)×|－| （4）‎ 4‎ ‎(5) (6) －4÷（－1）－[×（－）－（－0.5）]‎ ‎20、（5分）根据右边的数值转换器,当输入的满足时，请列式求出输出的结果. ‎ ‎21、（6分）如图已知正方形的边长为a，求阴影部分的面积.‎ ‎ ‎ ‎22、（6分）若(‎2a＋1)2与|b＋3|互为相反数，c是最大的负整数，求a3＋a2bc－a的值. ‎ 4‎ ‎23、（6分）某城市按以下规定收取每月煤气费，用煤气不超过60立方米，按每立方米0.8元收费；如果超过60立方米，超过部分按每立方米1.2元收费。如甲用户某月份用煤气80每立方米，那么这个月甲用户应交煤气费用为60×0.8＋（80-60）×1.2=72元。‎ ‎（1）设甲用户某月用煤气x立方米，用含x的代数式表示甲用户该月的煤气费.‎ ‎ (2) 若甲用户10月份的煤气费是84元,求甲用户10月份用去煤气多少立方米? ‎ ‎24、（9分）阅读材料，数学家高斯在上学时曾经研究过这样一个问题，1+2+3+…+10=？经过研究，这个问题的一般性结论是1+2+3+…+n=n（n+1），其中n为正整数，现在我们来研究一个类似的问题：1×2 + 2×3 +… + n（n+1）=？ ‎ 观察下面三个特殊的等式：‎ ‎1×2=（1×2×3-0×1×2）；2×3=（2×3×4-1×2×3）；3×4=（3×4×5-2×3×4）；将这三个等式的俩边相加，可以得到1×2+2×3+3×4=×3×4×5=20.‎ 读完这段材料，请你计算： ‎ ‎（1）1×2+2×3+…+100×101；（只需写出结果）‎ ‎（2）1×2+2×3+…+ n（n+1）；(写出计算过程) ‎ ‎（3）1001×1002+1002×1003+···+2013×2014(写出计算过程)‎ 4‎