2020年秋人教版七年级数学上册七年级上册 期中试卷（2） 19页

第 1页（共 19页） 2020 年秋人教版七年级数学上册期中试卷（2） 一、选择题（每小题 3 分，共 30 分） 1．（3 分）如果收入 200 元记作+200 元，那么支出 150 元记作（ ） A．+150 元 B．﹣150 元 C．+50 元 D．﹣50 元 2．（3 分）下列说法，其中正确的个数为（ ） ①正数和负数统称为有理数； ②一个有理数不是整数就是分数； ③有最小的负数，没有最大的正数； ④符号相反的两个数互为相反数； ⑤﹣a 一定在原点的左边． A．1 个 B．2 个 C．3 个 D．4 个 3．（3 分）数轴上有 A，B，C，D 四个点，其中绝对值相等的点是（ ） A．点 A 与点 D B．点 A 与点 C C．点 B 与点 C D．点 B 与点 D 4．（3 分）﹣2016 的相反数是（ ） A．﹣2016 B．2016 C．±2016 D． 5．（3 分）计算﹣32 的结果是（ ） A．9 B．﹣9 C．6 D．﹣6 6．（3 分）多项式 2x2y3﹣5xy2﹣3 的次数和项数分别是（ ） A．5，3 B．5，2 C．8，3 D．3，3 7．（3 分）若单项式﹣3a5b 与 am+2b 是同类项，则常数 m 的值为（ ） A．﹣3 B．4 C．3 D．2 8．（3 分）以下各图均有彼此连接的六个小正方形纸片组成，其中不能折叠成一 个正方体的是（ ） A． B． C． D． 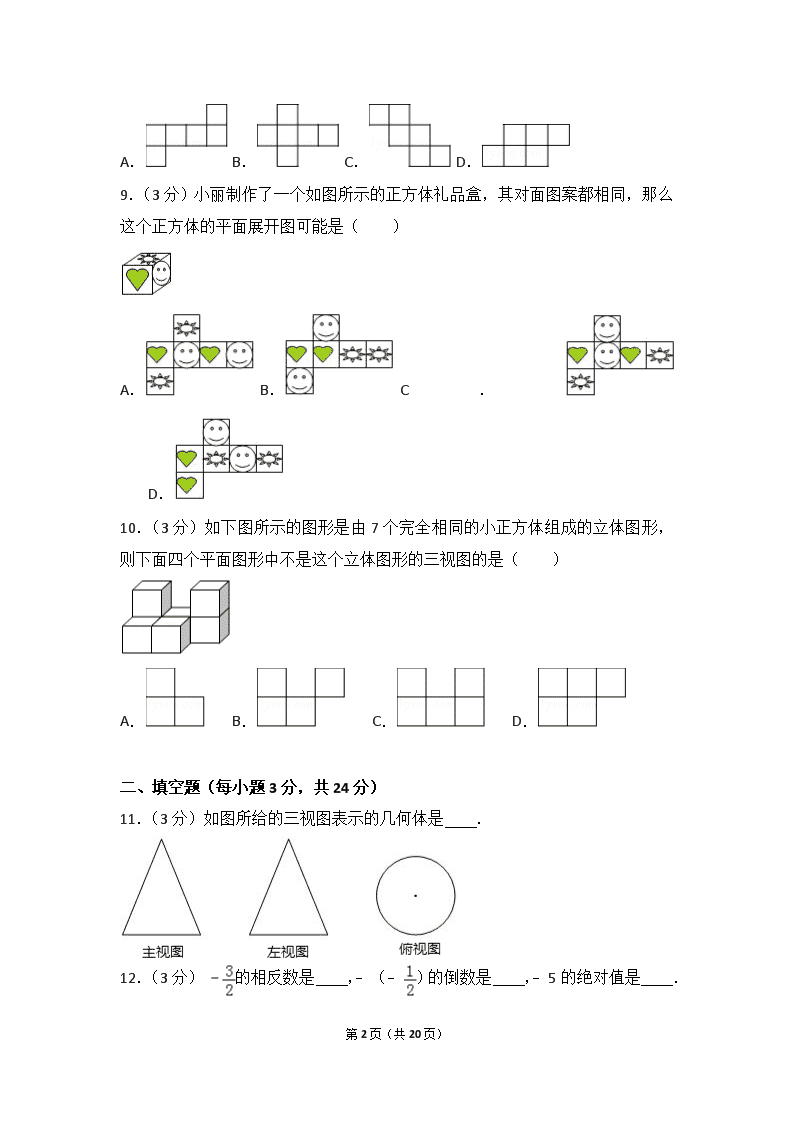9．（3 分）小丽制作了一个如图所示的正方体礼品盒，其对面图案都相同，那么 这个正方体的平面展开图可能是（ ） 第 2页（共 19页） A． B． C． D． 10．（3 分）如下图所示的图形是由 7 个完全相同的小正方体组成的立体图形， 则下面四个平面图形中不是这个立体图形的三视图的是（ ） A． B． C． D． 二、填空题（每小题 3 分，共 24 分） 11．（3 分）如图所给的三视图表示的几何体是 ． 12．（3 分） 的相反数是 ，﹣（﹣ ）的倒数是 ，﹣5 的绝对值是 ． 13．（3 分）据报道，春节期间微信红包收发高达 3270000000 次，则 3270000000 用科学记数法表示为 ． 14．（3 分）已知（x﹣2）2+|3y﹣2x|=0，则 x= ，y= ． 15．（3 分）用“＞”，“＜”，“=”填空： （1）0.7 0 （2）﹣6 4 （3） ﹣ ． 16．（3 分）已知|x|=3，则 x 的值是 ． 第 3页（共 19页） 17．（3 分）梯形的上底长为 8，下底长为 x，高是 6，那么梯形面积 y 与下底长 x 之间的关系式是 ． 18．（3 分）如图是一组有规律的图案，图案 1 是由 4 个 组成的，图案 2 是由 7 个 组成的，那么图案 5 是由 个 组成的，依此，第 n 个图案是由 个 组成的． 三、计算题（共 28 分） 19．（16 分）计算： （1）45﹣92+5﹣8 （2）（ ﹣ + ）×（﹣42） （3）2×（﹣5）+22﹣3÷ （4）﹣24+|6﹣10|﹣3×（﹣1）2014． 20．（12 分）先化简，再求值： （1）3x﹣4x2+7﹣3x+2x2+1，其中 x=﹣3． （2）3x2y﹣[2x2y﹣3（2xy﹣x2y）﹣xy]，其中 x=﹣1，y=﹣2． 四、解答题（21 题 5 分，22 题 4 分，23 题 6 分，24 题 7 分，25 题 8 分，26 题 8 分，共 38 分） 21．（5 分）（1）画出数轴，并用数轴上的点表示下列各数： ﹣5，2.5，3，﹣ ，0，﹣3，3 ． （2）用“＜”号把各数从小到大连起来： 22．（4 分）如果 x，y 满足|x|=3，|y|=2，求出 x+y 所有可能的值． 23．（6 分）如图，这是一个由小立方块塔成的几何体的俯视图，小正方形中的 数字表示该位置的小立方块的个数．请你画出它的主视图与左视图． 第 4页（共 19页） 24．（7 分）作图与推理：如图 1，是由一些大小相同的小正方体组合成的简单几 何体 （1）图 1 中有 块小正方体； （2）该几何体的主视图如图 2 所示，请在方格纸中分别画出它的左视图和俯视 图． 25．（8 分）司机小王沿东西大街跑出租车，约定向东为正，向西为负，某天自 A 地出发到收工时，行走记录为（单位：千米）：+8、﹣9、+7、﹣2、+5、﹣10、 +7、﹣3、 回答下列问题： （1）收工时小王在 A 地的哪边？距 A 地多少千米？ （2）若每千米耗油 0.2 升，问从 A 地出发到收工时，共耗油多少升？ （3）在工作过程中，小王最远离 A 地多远？ 26．（8 分）某餐厅中，一张桌子可坐 6 人，有以下两种摆放方式： （1）有 4 张桌子，用第一种摆设方式，可以坐 人；当有 n 张桌子时，用第 二种摆设方式可以坐 人（用含有 n 的代数式表示）． （2）一天中午，餐厅要接待 85 位顾客共同就餐，但餐厅中只有 20 张这样的长 方形桌子可用，且每 4 张拼成一张大桌子，若你是这家餐厅的经理，你打算选择 哪种方式来摆放餐桌，为什么？ 第 5页（共 19页） 第 6页（共 19页） 参考答案与试题解析 一、选择题（每小题 3 分，共 30 分） 1．（3 分）如果收入 200 元记作+200 元，那么支出 150 元记作（ ） A．+150 元 B．﹣150 元 C．+50 元 D．﹣50 元 【考点】正数和负数． 【分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表 示．“正”和“负”相对，所以，如果收入 200 元记作+200 元，那么支出 150 元记作 ﹣150 元． 【解答】解：因为正”和“负”相对，所以，如果收入 200 元记作+200 元，那么支 出 150 元记作﹣150 元． 故选 B． 【点评】解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量． 2．（3 分）下列说法，其中正确的个数为（ ） ①正数和负数统称为有理数； ②一个有理数不是整数就是分数； ③有最小的负数，没有最大的正数； ④符号相反的两个数互为相反数； ⑤﹣a 一定在原点的左边． A．1 个 B．2 个 C．3 个 D．4 个 【考点】有理数；相反数． 【分析】根据有理数的定义，有理数的分类，相反数的定义，数轴的认识即可求 解． 【解答】解：①正数，0 和负数统称为有理数，原来的说法错误； ②一个有理数不是整数就是分数是正确的； ③没有最小的负数，没有最大的正数，原来的说法错误； ④只有符号相反的两个数互为相反数，原来的说法错误； ⑤a＜0，﹣a 一定在原点的右边，原来的说法错误． 第 7页（共 19页） 其中正确的个数为 1 个． 故选 A． 【点评】本题考查有理数的定义，相反数的知识，属于基础题，注意概念的掌握， 及特殊例子的记忆． 3．（3 分）数轴上有 A，B，C，D 四个点，其中绝对值相等的点是（ ） A．点 A 与点 D B．点 A 与点 C C．点 B 与点 C D．点 B 与点 D 【考点】数轴；绝对值． 【专题】推理填空题． 【分析】根据数轴上绝对值相等的点到原点的距离相等，判断出数轴上有 A，B， C，D 四个点，其中绝对值相等的点是哪两个点即可． 【解答】解：∵点 B 与点 C 到原点的距离相等， ∴数轴上有 A，B，C，D 四个点，其中绝对值相等的点是点 B 与点 C． 故选：C． 【点评】此题主要考查了数轴的特征和应用，要熟练掌握，解答此题的关键是要 明确：数轴上绝对值相等的点到原点的距离相等． 4．（3 分）﹣2016 的相反数是（ ） A．﹣2016 B．2016 C．±2016 D． 【考点】相反数． 【分析】根据只有符号不同的两个数互为相反数，可得答案． 【解答】解：﹣2016 的相反数是 2016． 故选：B． 【点评】本题考查了相反数，在一个数的前面加上负号就是这个数的相反数． 5．（3 分）计算﹣32 的结果是（ ） A．9 B．﹣9 C．6 D．﹣6 【考点】有理数的乘方． 第 8页（共 19页） 【分析】根据有理数的乘方的定义解答． 【解答】解：﹣32=﹣9． 故选：B． 【点评】本题考查了有理数的乘方，是基础题，熟记概念是解题的关键． 6．（3 分）多项式 2x2y3﹣5xy2﹣3 的次数和项数分别是（ ） A．5，3 B．5，2 C．8，3 D．3，3 【考点】多项式． 【分析】根据多项式次数的定义求解，多项式的次数是多项式中最高次项的次数， 多项式中单项式的个数是多项式的项数，可得答案． 【解答】解：多项式 2x2y3﹣5xy2﹣3 的次数和项数分别是 5，3， 故选：A． 【点评】本题考查了多项式，解题的关键是弄清多项式次数是多项式中次数最高 的项的次数． 7．（3 分）若单项式﹣3a5b 与 am+2b 是同类项，则常数 m 的值为（ ） A．﹣3 B．4 C．3 D．2 【考点】同类项． 【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程求 得 m 的值． 【解答】解：根据题意得：m+2=5， 解得：m=3． 故选 C． 【点评】本题考查了同类项的定义，同类项定义中的两个“相同”：相同字母的指 数相同，是易混点，因此成了中考的常考点． 8．（3 分）以下各图均有彼此连接的六个小正方形纸片组成，其中不能折叠成一 个正方体的是（ ） 第 9页（共 19页） A． B． C． D． 【考点】展开图折叠成几何体． 【分析】由平面图形的折叠及正方体的展开图解题．能组成正方体的“一，四， 一”“三，三”“二，二，二”“一，三，二”的基本形态要记牢． 【解答】解：选项 A、B、C 都可以折叠成一个正方体； 选项 D，有“田”字格，所以不能折叠成一个正方体． 故选 D． 【点评】考查了展开图折叠成几何体，只要有“田”字格的展开图都不是正方体的 表面展开图． 9．（3 分）小丽制作了一个如图所示的正方体礼品盒，其对面图案都相同，那么 这个正方体的平面展开图可能是（ ） A． B． C． D． 【考点】几何体的展开图． 【分析】本题考查了正方体的展开与折叠．可以动手折叠看看，充分发挥空间想 象能力解决也可以． 【解答】解：根据题意及图示只有 A 经过折叠后符合． 故选：A． 【点评】本题着重考查学生对立体图形与平面展开图形之间的转换能力，与课程 标准中“能以实物的形状想象出几何图形，由几何图形想象出实物的形状”的要求 相一致，充分体现了实践操作性原则．要注意空间想象哦，哪一个平面展开图对 面图案都相同 第 10页（共 19页） 10．（3 分）如下图所示的图形是由 7 个完全相同的小正方体组成的立体图形， 则下面四个平面图形中不是这个立体图形的三视图的是（ ） A． B． C． D． 【考点】简单组合体的三视图． 【分析】根据几何体组成，结合三视图的观察角度，进而得出答案． 【解答】解：根据立方体的组成可得出： A、是几何体的左视图，故此选项错误； B、不是几何体的三视图，故此选项正确； C、是几何体的主视图，故此选项错误； D、是几何体的俯视图，故此选项错误； 故选：B． 【点评】此题主要考查了简单组合体的三视图，准确把握观察角度是解题关键． 二、填空题（每小题 3 分，共 24 分） 11．（3 分）如图所给的三视图表示的几何体是 圆锥 ． 【考点】由三视图判断几何体． 【专题】图表型． 【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形 状． 【解答】解：主视图和左视图都是等腰三角形，那么此几何体为锥体，由俯视图 为圆，可得此几何体为圆锥． 第 11页（共 19页） 【点评】主视图和左视图的大致轮廓为长方形的几何体为锥体． 12．（3 分） 的相反数是 ，﹣（﹣ ）的倒数是 2 ，﹣5 的绝对值是 5 ． 【考点】倒数；相反数；绝对值． 【分析】依据相反数、倒数、绝对值的定义回答即可． 【解答】解： 的相反数是 ；﹣（﹣ ）的倒数是 2，﹣5 的绝对值是 5． 故答案为： ；2；5． 【点评】本题主要考查的是倒数、相反数、绝对值的定义，熟练掌握相关概念是 解题的关键． 13．（3 分）据报道，春节期间微信红包收发高达 3270000000 次，则 3270000000 用科学记数法表示为 3.27×109 ． 【考点】科学记数法—表示较大的数． 【分析】科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确 定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点 移动的位数相同．当原数绝对值＞1 时，n 是正数；当原数的绝对值＜1 时，n 是负数． 【解答】解：将 3270000000 用科学记数法表示为 3.27×109． 故答案为：3.27×109． 【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为 a×10n 的 形式，其中 1≤|a|＜10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值． 14．（3 分）已知（x﹣2）2+|3y﹣2x|=0，则 x= 2 ，y= ． 【考点】非负数的性质：偶次方；非负数的性质：绝对值． 【分析】根据非负数的性质列式求解即可得到 x、y 的值． 【解答】解：由题意得，x﹣2=0，3y﹣2x=0， 解得 x=2，y= ． 第 12页（共 19页） 故答案为：2； ． 【点评】本题考查了非负数的性质：几个非负数的和为 0 时，这几个非负数都为 0． 15．（3 分）用“＞”，“＜”，“=”填空： （1）0.7 ＞ 0 （2）﹣6 ＜ 4 （3） ＞ ﹣ ． 【考点】有理数大小比较． 【专题】计算题． 【分析】（1）根据正数都大于 0 比较大小； （2）根据负数都小于 0 比较大小； （3）先计算|﹣ |= = ，|﹣ |= = ，然后根据负数的绝对值越大，这个 数越小比较大小． 【解答】解：（1）0.7＞0； （2）﹣6＜4； （3）∵|﹣ |= = ，|﹣ |= = ， ∴﹣ ＞﹣ ． 故答案为＞、＜、＞． 【点评】本题考查了有理数大小比较：正数大于 0，负数小于 0；负数的绝对值 越大，这个数越小． 16．（3 分）已知|x|=3，则 x 的值是 ±3 ． 【考点】绝对值． 【分析】根据绝对值相等的点有两个，可得答案． 【解答】解：|x|=3， 解得：x=±3； 故答案为：±3． 第 13页（共 19页） 【点评】本题考查了绝对值，绝对值相等的点有两个，注意不要漏掉． 17．（3 分）梯形的上底长为 8，下底长为 x，高是 6，那么梯形面积 y 与下底长 x 之间的关系式是 y=3x+24 ． 【考点】函数关系式． 【分析】根据梯形的面积公式：（上底+下底）×高÷2 进行计算即可． 【解答】解：根据梯形的面积公式可得 y=（x+8）×6÷2=3x+24， 故答案为：y=3x+24． 【点评】此题主要考查了函数关系式，关键是掌握梯形的面积公式． 18．（3 分）如图是一组有规律的图案，图案 1 是由 4 个 组成的，图案 2 是由 7 个 组成的，那么图案 5 是由 16 个 组成的，依此，第 n 个图案是由 3n+1 个 组成的． 【考点】规律型：图形的变化类． 【专题】压轴题；规律型． 【分析】观察不难发现，后一个图案比前一个图案多 3 个基础图形，然后写出第 5 个和第 n 个图案的基础图形的个数即可． 【解答】解：由图可得，第 1 个图案基础图形的个数为 4， 第 2 个图案基础图形的个数为 7，7=4+3， 第 3 个图案基础图形的个数为 10，10=4+3×2， …， 第 5 个图案基础图形的个数为 4+3（5﹣1）=16， 第 n 个图案基础图形的个数为 4+3（n﹣1）=3n+1． 故答案为：16，3n+1． 【点评】本题是对图形变化规律的考查，观察出“后一个图案比前一个图案多 3 个基础图形”是解题的关键． 第 14页（共 19页） 三、计算题（共 28 分） 19．（16 分）计算： （1）45﹣92+5﹣8 （2）（ ﹣ + ）×（﹣42） （3）2×（﹣5）+22﹣3÷ （4）﹣24+|6﹣10|﹣3×（﹣1）2014． 【考点】有理数的混合运算． 【分析】（1）将正数与负数分别结合，再根据有理数加法法则计算即可； （2）根据乘法分配律进行计算即可； （3）先算乘方，再算乘除，最后算加减即可； （4）先算乘方与绝对值，再算乘法，最后算加减即可． 【解答】解：（1）45﹣92+5﹣8 =45+（﹣92）+5+（﹣8） =45+5﹣（92+8） =﹣50； （2）（ ﹣ + ）×（﹣42） =﹣7+9﹣28 =﹣26； （3）2×（﹣5）+22﹣3÷ =﹣10+4﹣6 =﹣12； （4）﹣24+|6﹣10|﹣3×（﹣1）2014 =﹣16+4﹣3 =﹣15． 【点评】本题考查的是有理数的混合运算，熟知有理数混合运算的法则是解答此 题的关键． 第 15页（共 19页） 20．（12 分）先化简，再求值： （1）3x﹣4x2+7﹣3x+2x2+1，其中 x=﹣3． （2）3x2y﹣[2x2y﹣3（2xy﹣x2y）﹣xy]，其中 x=﹣1，y=﹣2． 【考点】整式的加减—化简求值． 【专题】计算题；整式． 【分析】（1）原式合并同类项得到最简结果，把 x 的值代入计算即可求出值； （2）原式去括号合并得到最简结果，把 x 与 y 的值代入计算即可求出值． 【解答】解：（1）3x﹣4x2+7﹣3x+2x2+1 =（3x﹣3x）+（﹣4x2+2x2）+（7+1） =﹣2x2+8， 当 x=﹣3 时，原式=﹣2x2+8=﹣18+8=﹣10； （2）3x2y﹣[2x2y﹣3（2xy﹣x2y）﹣xy] =3x2y﹣[2x2y﹣6xy+3x2y﹣xy] =3x2y﹣2x2y+6xy﹣3x2y+xy =3x2y﹣2x2y+6xy﹣3x2y+xy =﹣2x2y+7xy， 当 x=﹣1，y=﹣2 时，原式=﹣2x2y+7xy=﹣2×（﹣1）2×（﹣2）+7×（﹣1）× （﹣2）=18． 【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键． 四、解答题（21 题 5 分，22 题 4 分，23 题 6 分，24 题 7 分，25 题 8 分，26 题 8 分，共 38 分） 21．（5 分）（1）画出数轴，并用数轴上的点表示下列各数： ﹣5，2.5，3，﹣ ，0，﹣3，3 ． （2）用“＜”号把各数从小到大连起来： 【考点】有理数大小比较；数轴． 【专题】数形结合． 【分析】（1）利用数轴表示数的方法表示出所给的 7 个数； （2）利用数轴直接写出它们的大小关系． 第 16页（共 19页） 【解答】解：（1）如图： ； （2）它们的大小关系为﹣5＜﹣3＜0＜2.5＜3＜3 ． 【点评】本题考查了有理数大小比较：正数都大于 0；负数都小于 0； 正数大于 一切负数；两个负数，绝对值大的其值反而小．也考查了数轴． 22．（4 分）如果 x，y 满足|x|=3，|y|=2，求出 x+y 所有可能的值． 【考点】绝对值；有理数的加法． 【分析】首先根据绝对值的定义求得 x 和 y 的值，然后再求 x+y 的值，从而确定 答案． 【解答】解：∵|x|=3，|y|=2， ∴x=±3，y=±2， ∴x+y=3+2=5 或 x+y=3+（﹣2）=1 或 x+y=﹣3+2=﹣1 或 x+y=﹣3﹣2=﹣5． 【点评】本题考查了绝对值的知识，解题的关键是确定 x，y 的值． 23．（6 分）如图，这是一个由小立方块塔成的几何体的俯视图，小正方形中的 数字表示该位置的小立方块的个数．请你画出它的主视图与左视图． 【考点】作图-三视图；由三视图判断几何体． 【分析】主视图有 3 列，每列小正方形数目分别为 3，2，4；左视图有 3 列，每 列小正方形数目分别为 2，3，4．依此画出图形即可求解． 【解答】解：如图所示： 第 17页（共 19页） 【点评】本题考查实物体的三视图．在画图时一定要将物体的边缘、棱、顶点都 体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．本题画 几何体的三视图时应注意小正方形的数目及位置． 24．（7 分）作图与推理：如图 1，是由一些大小相同的小正方体组合成的简单几 何体 （1）图 1 中有 11 块小正方体； （2）该几何体的主视图如图 2 所示，请在方格纸中分别画出它的左视图和俯视 图． 【考点】作图-三视图；由三视图判断几何体． 【分析】（1）找到所有正方体的个数，让它们相加即可； （2）主视图有 4 列，每列小正方形数目分别为 2，2，2，1；左视图有 2 列，每 列小正方形数目分别为 2，2；俯视图有 4 列，每列小正方形数目分别为 2，2，1， 1． 【解答】解：（1）2×5+1=11（块）． 故图 1 中有 11 块小正方体； （2）如图所示： 第 18页（共 19页） 故答案为：11． 【点评】本题考查了作三视图，主视图、左视图、俯视图是分别从物体正面、左 面和上面看，所得到的图形． 25．（8 分）司机小王沿东西大街跑出租车，约定向东为正，向西为负，某天自 A 地出发到收工时，行走记录为（单位：千米）：+8、﹣9、+7、﹣2、+5、﹣10、 +7、﹣3、 回答下列问题： （1）收工时小王在 A 地的哪边？距 A 地多少千米？ （2）若每千米耗油 0.2 升，问从 A 地出发到收工时，共耗油多少升？ （3）在工作过程中，小王最远离 A 地多远？ 【考点】正数和负数． 【分析】（1）根据有理数的加法，可得答案； （2）根据单位耗油量乘以行驶路程，可得耗油量； （3）根据有理数的加法，可得每次与 A 地的距离，根据有理数的大小比较，可 得答案． 【解答】解：（1）8+（﹣9）+7+（﹣2）+5+（﹣10）+7+（﹣3）=3（千米）， 答：收工时小王在 A 地的东边，距 A 地 3 千米； （2）0.2×（8+|﹣9|+7+|﹣2|+5+|﹣10|+7+|﹣3|）=0.2×51=10.2（升）， 答：从 A 地出发到收工时，共耗油 10.2 升； （3）第一次距 A 地 8 千米，第二次距 A 地|8+（﹣9）+=|﹣1+=1 千米，第三次 距 A 地﹣1+7=6 千米，第四次距 A 地 6+（﹣2）=4 千米，第五次距 A 地 4+5=9 千米，第六次距 A 地|9+（﹣10）|=1 千米，第七次距 A 地﹣1+7=6 千米，第八 次距 A 地 6+（﹣3）=4 千米， 由 9＞8＞6＞4＞1， 在工作过程中，小王最远离 A 地 9 千米． 【点评】本题考查了正负数，单位耗油量乘以行驶路程是解题关键，注意与 A 地的距离是点与 A 地的绝对值． 第 19页（共 19页） 26．（8 分）某餐厅中，一张桌子可坐 6 人，有以下两种摆放方式： （1）有 4 张桌子，用第一种摆设方式，可以坐 18 人；当有 n 张桌子时，用 第二种摆设方式可以坐 2n+4 人（用含有 n 的代数式表示）． （2）一天中午，餐厅要接待 85 位顾客共同就餐，但餐厅中只有 20 张这样的长 方形桌子可用，且每 4 张拼成一张大桌子，若你是这家餐厅的经理，你打算选择 哪种方式来摆放餐桌，为什么？ 【考点】规律型：图形的变化类． 【分析】（1）第一种中，只有一张桌子是 6 人，后边多一张桌子多 4 人．即有 n 张桌子时是 6+4（n﹣1）=4n+2，由此算出 4 张桌子，用第一种摆设方式，可以 坐 4×4+2=18 人； 第二种中，有一张桌子是 6 人，后边多一张桌子多 2 人，即 6+2（n﹣1）=2n+4． （2）分别求出 n=20 时，两种不同的摆放方式对应的人数，即可作出判断． 【解答】解：（1）有 4 张桌子，用第一种摆设方式，可以坐 18 人；当有 n 张桌 子时，用第二种摆设方式可以坐 2n+4 人； （2）选择第一种方式来摆餐桌． 理由如下： ∵第一种方式，4 张桌子拼在一起可坐 18 人． 20 张桌子可拼成 5 张大桌子，共可坐：18×5=90（人）． 第二种方式，4 张桌子拼在一起可坐 12 人． 20 张桌子可拼成 5 张大桌子，共可坐：12×5=60（人）． 又∵90＞85＞60 ∴应选择第一种方式来摆餐桌． 【点评】此题考查图形的变化规律，找出图形之间的联系，得出运算规律，利用 规律解决问题．