人教版数学七下《相交线》基础测试题 6页

相交线专训题 姓名 1、下列说法正确的是（ ） A、相等的角是对顶角 B、若两个角不是对顶角，则这两个角不相等 C、邻补角一定互补 D、互补的两角一定是邻补角 2、如果两个角互为补角，那么这两个角（ ） A、一个锐角，一个直角 B、都是锐角 C、一个锐角，一个钝角或两个直角 D、都是直角 3、如图 1，直线 AB 、CD 、EF 都经过点O ，则 321  等于（ ） A、 90 B、 120 C、 180 D、 360 4、如图 2，已知直线 AB ，CD 相交于点O ， CDOE  ，垂足是 O ，则 图中 AOE 与 BOD 的关系是（ ） A、互为邻补角 B、对顶角 C、互补 D、互余 5、下列说法中，错误的是（ ） A、过一点有且只有一条直线与已知直线垂直 B、互为邻补角的两个角的平分线互相垂直 C、垂线段最短 D、过直线外一点有无数条线段与已知直线垂直 6、如图 3，  90BAC ， BCAD  ，则下列的结论中：①点 B 到 AC 的 垂线段是 AB ；②线段 AC 是点C 到 AB 的垂线段；③线段 AD 是点 D 到 BC 的垂线段；④线段 BD 是点 B 到 AD 的垂线段，其中正确的个数是（ ） A、1 B、2 C、3 D、4 7、 在 2009 年 23 日进行的柏林田径世锦赛女子跳远决赛中，美国选手 22 岁的里斯是以 7 米 01 的成绩赢得了金牌。裁判测量跳远成绩的依据是（ ） A 平行线间的距离相等 B 两点之间，线段最短 C 垂线段最短 D 两点确定一条直线 8、如果  、  是对顶角且互补，则它们所在的直线（ ） A 互相垂直 B 互相平行 C 既不垂直也不相交 D 不能确定 9、如图，下列判断中错误的是（ ） A ∠1、∠2 是同旁内角 B ∠3、∠4 是内错角 C ∠5、∠6 是同位角 D ∠4、∠5 是同旁内角 6 5 4 3 2 1 10、满足下列关系的两个角，一定相等的是（ ） A 同旁内角 B 同位角 C 对顶角 D 内错角 11、已知 1 与  互余，  与 3 是邻补角，如果  651 ，那么 。 12、如图 8 所示，从河中向稻田 A 处引水，为了使水渠最短，可以过 A 点作 CDAB  于 B ， 沿线段 AB 修水渠即可，其依据是 。 3 2 1 F E D C BA 图 1 E D C O BA 图 2 图 3 D CB A 图 8 DC B A 13、如图 12，直线 AB 、CD 交于点O ， AOCEOA  ， （1）指出 BOD 的对顶角； （2）指出 BOC 的补角； （3）若 EOA 与 EOD 的度数之比为 1：4，求 BOD 及其邻补角的 度数。 14、如图 15 所示，在公路l 的同侧有两个村庄 A 和 B ，小明住在 A 村， 小军住在 B 村，一天小明先去找小军，一起到公路l 搭车去县城办事，小 明要少走路，应在何处等车？请在图中画出来。 15、如图 16，直线 AB 、CD 交于点O ， ABOE  于O ，OB 平分 DOF ，  50DOE ，求 AOC 、 EOF 、 COF 的度数。 16、如图 17，点O 是直线 AB 上一点，过点O 任作一条射线OC ，OD 、OE 分别平分 AOC 和 BOC ，试确定OD 与OE 的位置关系，并说明理由。 17、如图 13，已知在这个图形中完成下列作图： （1）作出点 A 到 BC 的垂线段 AD ，并量出点 A 到直线 BC 的距离； (2)过点 B 作 AC 的垂线、垂足为 E ；过点C 作 AB 的垂线，垂足为 F ； (3)延长垂线段 DA ，你发现什么有趣的结论？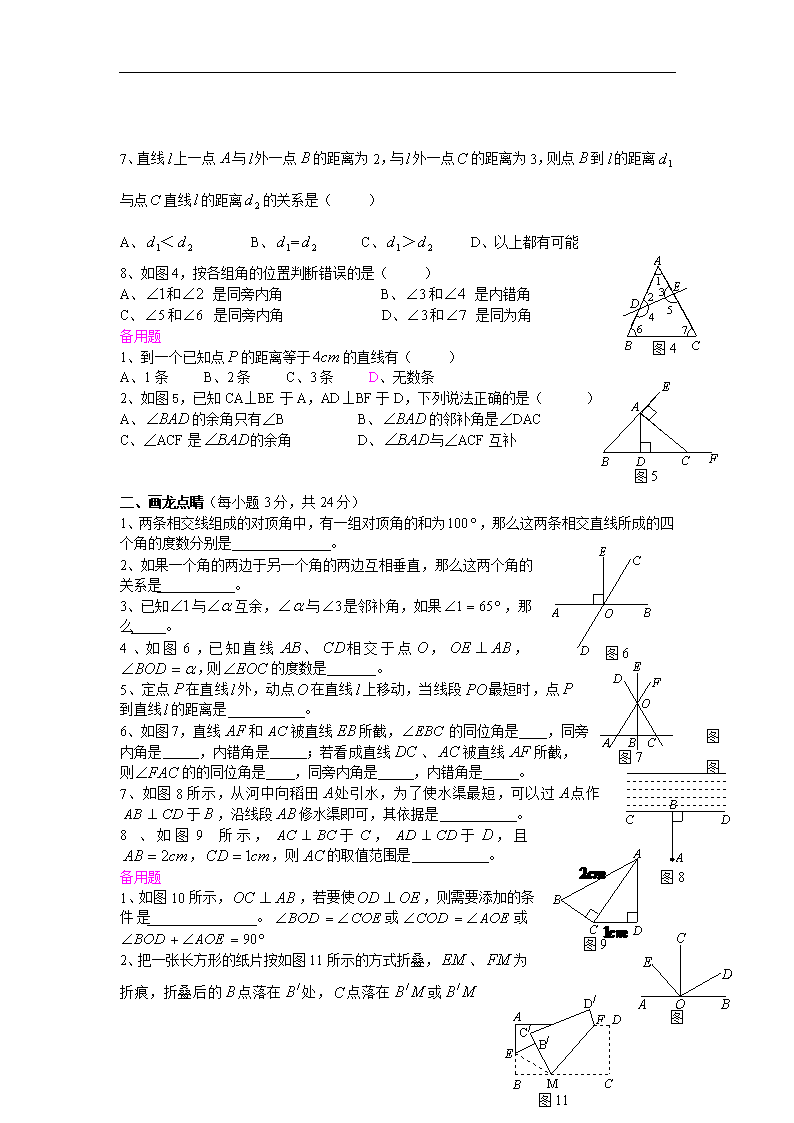 图 16 O F E D C BA 图 12 O E D C BA 图 15 B A 图 13 C B A 图 17 O E D C BA 7、直线l 上一点 A 与l 外一点 B 的距离为 2，与l 外一点C 的距离为 3，则点 B 到l 的距离 1d 与点C 直线l 的距离 2d 的关系是（ ） A、 1d ＜ 2d B、 1d = 2d C、 1d ＞ 2d D、以上都有可能 8、如图 4，按各组角的位置判断错误的是（ ） A、 1 和 2 是同旁内角 B、 3 和 4 是内错角 C、 5 和 6 是同旁内角 D、 3 和 7 是同为角 备用题 1、到一个已知点 P 的距离等于 cm4 的直线有（ ） A、1 条 B、2 条 C、3 条 D、无数条 2、如图 5，已知 CA⊥BE 于 A，AD⊥BF 于 D，下列说法正确的是（ ） A、 BAD 的余角只有∠B B、 BAD 的邻补角是∠DAC C、∠ACF 是 BAD 的余角 D、 BAD 与∠ACF 互补 二、画龙点睛（每小题 3 分，共 24 分） 1、两条相交线组成的对顶角中，有一组对顶角的和为 100 ，那么这两条相交直线所成的四 个角的度数分别是 。 2、如果一个角的两边于另一个角的两边互相垂直，那么这两个角的 关系是 。 3、已知 1 与  互余，  与 3 是邻补角，如果  651 ，那 么 。 4 、 如 图 6 ， 已 知 直 线 AB 、 CD 相 交 于 点 O ， ABOE  ， BOD ，则 EOC 的度数是 。 5、定点 P 在直线l 外，动点O 在直线l 上移动，当线段 PO 最短时，点 P 到 直线l 的距离是 。 6、如图 7，直线 AF 和 AC 被直线 EB 所截， EBC 的同位角是 ，同 旁内角是 ，内错角是 ；若看成直线 DC 、 AC 被直线 AF 所截， 则 FAC 的的同位角是 ，同旁内角是 ，内错角是 。 7、如图 8 所示，从河中向稻田 A 处引水，为了使水渠最短，可以过 A 点作 CDAB  于 B ，沿线段 AB 修水渠即可，其依据是 。 8、如图 9 所示， BCAC  于C ， CDAD  于 D ，且 cmAB 2 ， cmCD 1 ，则 AC 的取值范围是 。 备用题 1、如图 10 所示， ABOC  ，若要使 OEOD  ，则需要添加的 条件是 。 COEBOD  或 AOECOD  或  90AOEBOD 2、把一张长方形的纸片按如图 11 所示的方式折叠， EM 、 FM 为 折痕，折叠后的 B 点落在 /B 处，C 点落在 MB / 或 MB / 的 图 12 图 13 图 4 76 54 32 1 E D CB A 图 6 O E D C BA 图 7 O F E D CBA 图 9 DC B A 图 8 DC B A 图 10 O E D C BA 图 11 C/ D/ B/ M F E D CB A 图 5 F E D CB A 延长线上，那么 EMF 的度数是 。 90 三、考考你的基本功（本大题共 28 分） 1、如图 12，直线 AB 、CD 交于点O ， AOCEOA  ， （1）指出 BOD 的对顶角； （2）指出 BOC 的补角； （3）若 EOA 与 EOD 的度数之比为 1：4，求 BOD 及其邻补角的 度数。 2、如图 13，已知在这个图形中完成下列作图： （1）作出点 A 到 BC 的垂线段 AD ，并量出点 A 到直线 BC 的距离； (2)过点 B 作 AC 的垂线、垂足为 E ；过点C 作 AB 的垂线，垂足为 F ； (3)延长垂线段 DA ，你发现什么有趣的结论？ 3、如图 14，直线 AB 、CD 交于点O ，写出 BOC ， BOD ， AOD ， BDO 中每两个角之间的位置关系。 四、同步大闯关（本大题共 24 分） 1、如图 15 所示，在公路l 的同侧有两个村庄 A 和 B ，小明住在 A 村， 小军住在 B 村，一天小明先去找小军，一起到公路l 搭车去县城办事， 小明要少走路，应在何处等车？请在图中画出来。 2、如图 16，直线 AB 、 CD 交于点 O ， ABOE  于 O ， OB 平分 DOF ，  50DOE ，求 AOC 、 EOF 、 COF 的度数。 图 13 C B A 图 15 B A 图 16 O F E D C BA 图 14 O D C B A 图 12 O E D C BA 五、能力提升 超越自我 1、如图 17，点O 是直线 AB 上一点，过点 O 任作一条射线OC ，OD 、OE 分别平分 AOC 和 BOC ，试确定 OD 与OE 的位置关系，并说明理由。 2、如图 18 所示是一个跳棋棋盘，其游戏规则是：一个棋子从某一个起始角开始，经过若干 步跳动后，到达终点角，跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上， 下面给出两种从起始位置 1 跳到终点位置 3 的路径： 路径 1： 1  同旁内角 9  内错角 3 ； 路径 2： 1  内错角 12  内错角 3106    同旁内角同位角 。 （1）写出从 1 到 8 途径一个角的一条路径； （2）从起始 1 依次按同位角、内错角、同旁内角的顺序跳，能否跳到终 点 8 ； （3）找出从起始 1 跳到终点 8 的路径，要求跳遍所有的角，且不能重 复。 5.1 相交线水平测试水平测试答案 一、1、C；2、D；3、C；4、D；5、D；6、C；7、D；8、C；二、1、  130,50,130,50 ； 2、相等或互补；3、 153 ；4、  90 ；5、线段 PO 的长度；6、 EOF ， FOB ， AOB ， FOC ， DOA ， COA ；7、垂线段最短；8、 cm1 ＜ AC ＜ cm2 ；三、1、（1） AOC ； （2） EOA ， AOC ， BOD ；（3）  30BOD ， BOD 的邻补角是 150 ；2、作 图略，结论为可发现 CFBEDA 、、 交于同一点；3、 BOC 与 BOD 是邻补角， BOC 与 AOD 是对顶角， BOC 与 BDO 同位角； BOD 与 AOD 是邻补角， BOD 与 BDO 同旁内角； AOD 与 BDO 是内错角；四、1、作图略，过点 B 画l 的垂线，垂 足 C 为等车的位置，连接 AB ，小明沿 A → B → C 的路线行走，路程最短；2、解：由 ABOE  ，  50DOE ， 可 得  40BOD ， 因 为 OB 平 分 DOF ， 得  40BODBOF ， 根 据 对 顶 角 相 等 ， 可 得  40BODAOC ， 所 以  130404050BOFDOBDOEEOF ， 由 邻 补 角 的 定 义 可 得  10080180DOFCODCOF ；五、1、解： OEOD  ，理由：因为OD 、 OE 分 别平 分 AOC 和 BOC ， 所以 BOCCOEAOCDOC  2 1 2 1 , ， 所以  90180)( 2 1 2 1 2 1 2 1 2 1 AOBBOCAOCBOCAOCCOEDOCDOE ，即 图 18 12 1110 9 8 7 6 54 3 2 1 图 17 O E D C BA OEOD  ；2、（1）答案不唯一，如 1 → 9 → 8 ；（2）能，路径是; 1 → 10 → 5 → 8 ；（3）路径是： 1 → 9 → 2 → 10 → 3 → 4 → 11 → 5 → 6 → 12 → 7 → 8 。 图 5 图 6 图 7 图 8 图 12 图 13