七年级下册数学教案7-1-2 平面直角坐标系 人教版 5页

第七章 平面直角坐标系 ‎7.1 平面直角坐标系 教学备注 ‎【自学指导提示】‎ 学生在课前完成自主学习部分 ‎1.情景引入 ‎（见幻灯片3）‎ ‎2.探究点1新知讲授 ‎（见幻灯片4-14）‎ ‎7.1.2 平面直角坐标系 学习目标：1.了解平面直角坐标系的有关概念并能正确画出平面直角坐标系.‎ ‎2.通过小组合作、展示质疑，经历画坐标系、描点、连线等过程，培养数形结合思想和运用数学知识解决简单实际问题的能力.‎ 重点：在给定的平面直角坐标系中，会根据描点的位置写出点的坐标；坐标平面上点的坐标的特点.‎ 难点：根据坐标描出点的位置，由点的位置写出坐标.‎ 自主学习 一、知识链接 ‎1.什么是数轴？数轴上的点与实数有什么关系？‎ ‎2.如何确定直线上点的位置？‎ ‎3.平面内确定一个位置需要几个数据？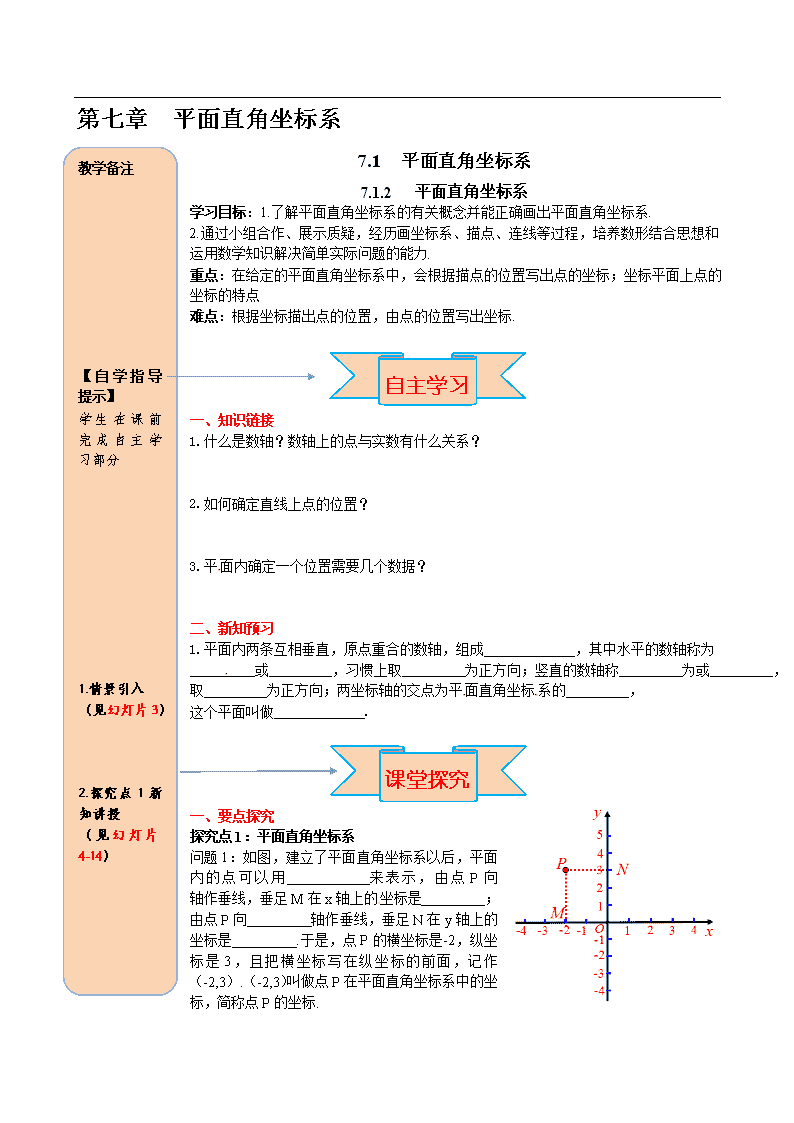‎ 二、新知预习 ‎1.平面内两条互相垂直，原点重合的数轴，组成 ，其中水平的数轴称为 ‎ 或 ，习惯上取 为正方向；竖直的数轴称 为或 ，取 为正方向；两坐标轴的交点为平面直角坐标系的 ，‎ 这个平面叫做 .[来源:学科网ZXXK][来源:Z*xx*k.Com]‎ 课堂探究 一、 要点探究 探究点1：平面直角坐标系 问题1：如图，建立了平面直角坐标系以后，平面内的点可以用 来表示，由点P向 轴作垂线，垂足M在x轴上的坐标是 ；由点P向 轴作垂线，垂足N在y轴上的坐标是 .于是，点P的横坐标是-2，纵坐标是3，且把横坐标写在纵坐标的前面，记作（-2,3）.（-2,3）叫做点P在平面直角坐标系中的坐标，简称点P的坐标. 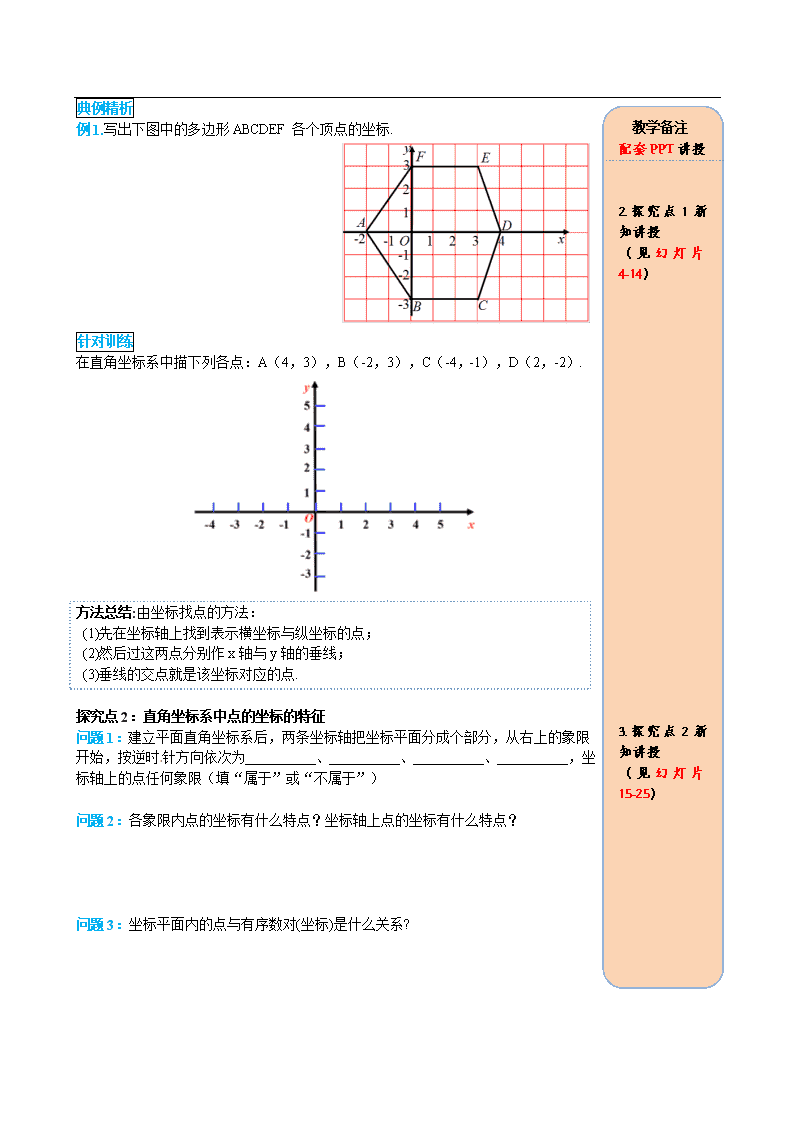‎ 教学备注 配套PPT讲授 ‎2.探究点1新知讲授 ‎（见幻灯片4-14）‎ ‎3.探究点2新知讲授 ‎（见幻灯片15-25）‎ 典例精析 例1.写出下图中的多边形ABCDEF各个顶点的坐标.‎ ‎ ‎ 针对训练 在直角坐标系中描下列各点：A（4，3），B（-2，3），C（-4，-1），D（2，-2）.‎ 方法总结:由坐标找点的方法：‎ ‎ (1)先在坐标轴上找到表示横坐标与纵坐标的点；‎ ‎ (2)然后过这两点分别作x轴与y轴的垂线；‎ ‎ (3)垂线的交点就是该坐标对应的点.‎ 探究点2：直角坐标系中点的坐标的特征 问题1：建立平面直角坐标系后，两条坐标轴把坐标平面分成个部分，从右上的象限开始，按逆时针方向依次为 、 、 、 ，坐标轴上的点任何象限（填“属于”或“不属于”）‎ 问题2：各象限内点的坐标有什么特点？坐标轴上点的坐标有什么特点？‎ 问题3：坐标平面内的点与有序数对(坐标)是什么关系?‎ 教学备注 配套PPT讲授 ‎3.探究点2新知讲授 ‎（见幻灯片15-25）‎ 典例精析 例2.在平面直角坐标系中，描出下列各点，并指出它们分别在哪个象限. A(5，4)，B(-3，4)，C (-4 ，-1)，D(2，-4).‎ 例3..设点M(a，b)为平面直角坐标系内的点．‎ ‎(1)当a>0，b<0时，点M位于第几象限？‎ ‎(2)当ab>0时，点M位于第几象限？‎ ‎(3)当a为任意有理数，且b<0时，点M位于第几象限？‎ 例4.点A(m＋3，m＋1)在x轴上，则A点的坐标为(　　)‎ A．(0，－2) B．(2，0) C．(4，0) D．(0，－4)‎ ‎ 方法总结：坐标轴上的点的坐标特点：x轴上的点的纵坐标为0，y轴上的点的横坐标为0.根据点所在坐标轴确定字母取值，进而求出点的坐标．‎ 针对训练 ‎1.已在平面直角坐标系中，点P(m，m－2)在第一象限内，则m的取值范围是________．‎ ‎ [来源:学科网ZXXK]‎ 方法总结：求点的坐标中字母的取值范围的方法：根据各个象限内点的坐标的符号特征，列出关于字母的不等式或不等式组，解不等式或不等式组即可求出相应字母的取值范围．‎ ‎ ‎ ‎2.已知点P到x轴的距离为2，到y轴的距离为1.如果过点P作两坐标轴的垂线，垂足分别在x轴的正半轴上和y轴的负半轴上，那么点P的坐标是(　　)‎ A.(2，－1) B.(1，－2) C.(－2，－1) D.(1，2)‎ 方法总结：本题的易错点有三处：‎ ‎①混淆距离与坐标之间的区别；‎ ‎②不知道“点P到x轴的距离”对应的是纵坐标，“点P到y轴的距离”对应的是横坐标；‎ ‎③忽略坐标的符号出现错解．若本例题只已知距离而无附加条件，则点P的坐标有四个．‎ 教学备注 配套PPT讲授 ‎4.探究点3新知讲授 ‎（见幻灯片26-31）‎ ‎5.课堂小结 探究点3：建立坐标系求图形中点的坐标 问题1：正方形ABCD的边长为4，请建立一个平面直角坐标系，并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.‎ 问题2：建立的平面直角坐标系不同，则各点的坐标也不同．你认为怎样建立直角坐标系才比较适当？‎ 总结归纳：建立平面直角坐标系，一般要使图形上的点的坐标容易确定，例如以正方形的两条边所在的直线为坐标轴，建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系．需要说明的是，虽然建立不同的平面直角坐标系，同一个点会有不同的坐标，但正方形的形状和性质不会改变．‎ ‎ ‎ 典例精析 例5.长方形的两条边长分别为4，6，建立适当的直角坐标系，使它的一个顶点的坐标为(－2，－3)．请你写出另外三个顶点的坐标．‎ 针对训练 右图是一个围棋棋盘(局部)，把这个围棋棋盘放置在一个平面直角坐标系中，白棋①的坐标是(－2，－1)，白棋③的坐标是(－1，－3)，则黑棋❷的坐标是________．‎ 二、课堂小结 ‎[来源:学|科|网Z|X|X|K]‎ 平面直角坐标系 定义 点的坐标特征 建立合适的平面直角坐标系 教学备注 配套PPT讲授 ‎6.当堂检测 ‎（见幻灯片32-35）‎ ‎ ‎当堂检测 ‎1.如图，点A的坐标为( )[来源:Z+xx+k.Com]‎ A.( -2，3) B.( 2，-3) C.( -2，-3) D.( 2，3)‎ ‎ 第1题图 第2题图 ‎2.如图，点A的坐标为 ，点B的坐标为 .‎ ‎3.在 y轴上的点的横坐标是 ，在 x轴上的点的纵坐标是 .‎ ‎4.点 M（- 8，12）到 x轴的距离是 ，到 y轴的距离是 . ‎ ‎5.下列各点分别在坐标平面的什么位置上？‎ A（3，6），B（0，－8），C（－7，－5），D（－6，0），E（－3.6，5），‎ F（5，－6），G（0，0）‎ ‎【拓展题】‎ ‎1.已知a