浙教版数学七年级上册《有理数的混合运算》练习题 4页

2．6 有理数的混合运算 1．形如|a c b d|的式子叫做二阶行列式，它的运算法则用公式表示为|a c b d|＝ad－bc，依此 法则计算|2 －1 －3 4|的结果为(C) A．11 B．－11 C．5 D．－2 2．计算1 3 ÷(－3)× －1 3 ×33 的结果为(A) A．1 B．9 C．27 D．－3 3．下列各组数中最大的数是(D) A．3×32－2×22 B．(3×3)2－2×22 C．(32)2－(22)2 D．(33)2－(22)2 4．计算 1 6 －1 2 －1 3 ×24 的结果为__－16__． 5．若(a－4)2＋|2－b|＝0，则 ab＝__16__， a＋b 2a－b ＝__1__． 6．计算： (1)(23－3)×4 5 ＝__4__； (2)(－4)÷(－3)×1 3 ＝__4 9 __． 7．若 n 为正整数，则（－1）n＋（－1）n＋1 2 ＝__0__． 8．计算： (1)－0.752÷ －11 2 3 ＋(－1)12× 1 2 －1 3 2 ； (2)[（－3）2－（－5）2]÷(－2)； (3)(－6)÷6 5 － （－3）3－ 1－0.25÷1 2 ×18. 【解】 (1)原式＝－ 3 4 2 ÷ －3 2 3 ＋(－1)12× 1 6 2 ＝－ 9 16 ÷ －27 8 ＋1× 1 36 ＝ 9 16 × 8 27 ＋ 1 36 ＝1 6 ＋ 1 36 ＝ 7 36 . (2)原式＝(9－25)÷(－2)＝(－16)÷(－2)＝16×1 2 ＝8. (3)原式＝－6×5 6 － －27－ 1－1 2 ×18＝－5＋495＝490. 9．对于任意有理数 a，b，规定一种新的运算：a*b＝a2＋b2－a－b＋1，则(－3)*5＝__33__． 【解】 (－3)*5＝(－3)2＋52－(－3)－5＋1 ＝9＋25＋3－5＋1 ＝33. 10．已知 4 个矿泉水空瓶可以换矿泉水一瓶，现有 16 个矿泉水空瓶，若不交钱，最多可以 喝矿泉水(C) A．3 瓶 B．4 瓶 C．5 瓶 D．6 瓶 【解】 16 个矿泉水瓶换 4 瓶矿泉水，再把喝完的 4 个空瓶再换一瓶水，共 5 瓶，故选 C. 11．已知 2a－b＝4，则 2(b－2a)2－3(b－2a)＋1＝__45__． 【解】 ∵2a－b＝4，∴b－2a＝－4. 原式＝2×(－4)2－3×(－4)＋1 ＝45. 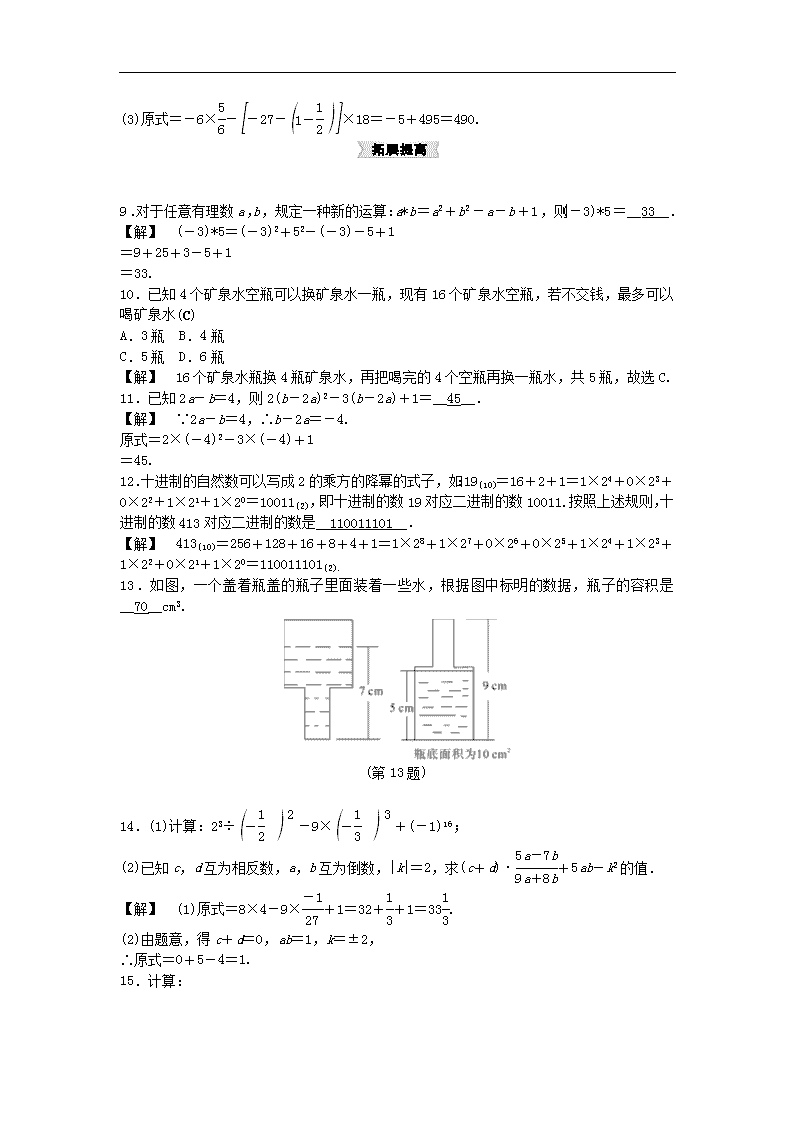12．十进制的自然数可以写成 2 的乘方的降幂的式子，如：19(10)＝16＋2＋1＝1×24＋0×23 ＋0×22＋1×21＋1×20＝10011(2)，即十进制的数 19 对应二进制的数 10011.按照上述规则， 十进制的数 413 对应二进制的数是__110011101__． 【解】 413(10)＝256＋128＋16＋8＋4＋1＝1×28＋1×27＋0×26＋0×25＋1×24＋1×23＋ 1×22＋0×21＋1×20＝110011101(2)． 13．如图，一个盖着瓶盖的瓶子里面装着一些水，根据图中标明的数据，瓶子的容积是 __70__cm3. (第 13 题) 14．(1)计算：23÷ －1 2 2 －9× －1 3 3 ＋(－1)16； (2)已知 c，d 互为相反数，a，b 互为倒数，|k|＝2，求(c＋d)·5a－7b 9a＋8b ＋5ab－k2 的值． 【解】 (1)原式＝8×4－9×－1 27 ＋1＝32＋1 3 ＋1＝331 3 . (2)由题意，得 c＋d＝0，ab＝1，k＝±2， ∴原式＝0＋5－4＝1. 15．计算： 1 1×2×3 ＋ 1 2×3×4 ＋ 1 3×4×5 ＋…＋ 1 11×12×13 . 【解】 原式＝1 2 1 1×2 － 1 2×3 ＋1 2 1 2×3 － 1 3×4 ＋1 2 1 3×4 － 1 4×5 ＋…＋1 2 1 11×12 － 1 12×13 ＝1 2 1 1×2 － 1 2×3 ＋ 1 2×3 － 1 3×4 ＋ 1 3×4 － 1 4×5 ＋…＋ 1 11×12 － 1 12×13 ＝1 2 1 1×2 － 1 12×13 ＝ 77 312 . 16．阅读材料，思考后请试着完成计算： 大数学家高斯在上学读书时曾经研究过这样一个问题：1＋2＋3＋…＋100＝？经过研究，这 个问题的一般性结论是 1＋2＋3＋…n＝1 2 n(n＋1)，其中 n 是正整数． 现在我们来研究一个类似的问题：1×2＋2×3＋…n(n＋1)＝？ 观察下面三个特殊的等式： 1×2＝1 3 (1×2×3－0×1×2)； 2×3＝1 3 (2×3×4－1×2×3)； 3×4＝1 3 (3×4×5－2×3×4)． 将这三个等式的两边相加，可以得到 1×2＋2×3＋3×4＝1 3 ×3×4×5＝20. 读完这段材料，请计算： (1)1×2＋2×3＋…＋100×101； (2)1×2＋2×3＋…＋2015×2016. 【解】 (1)1×2＋2×3＋…＋100×101 ＝1 3 (1×2×3－0×1×2)＋1 3 (2×3×4－1×2×3)＋…＋1 3 (100×101×102－99×100×101) ＝1 3 (100×101×102－0×1×2) ＝343400. (2)同理于(1)，原式＝1 3 (2015×2016×2017－0×1×2)＝2731179360.