[精] 华师大版 数学七年级下册 课件 8 一元一次不等式 20页

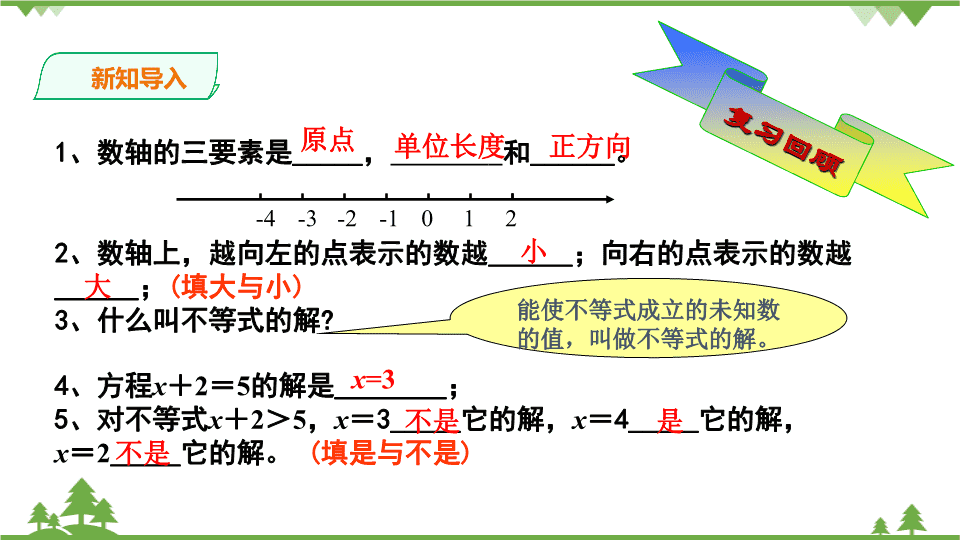
第八章 一元一次不等式 1、正确理解不等式的解、不等式的解集，解不等式的概念、 掌握在数轴上表示不等式的解的集合的方法。 2、培养学生观察，分析，比较的能力，并出初步掌握对比的 思想方法。 3、在本节课的教学过程中，渗透数形结合的思想，并使学生 初步学会运用数学结合的观点去分析问题，解决问题。 新知导入 1、数轴的三要素是_____， 和______。 2、数轴上，越向左的点表示的数越______；向右的点表示的数越 ______；(填大与小) 3、什么叫不等式的解? 4、方程x＋2＝5的解是________； 5、对不等式x＋2＞5，x＝3_____它的解，x＝4_____它的解， x＝2_____它的解。 (填是与不是) -2 -1 0 1 2-3-4 原点 单位长度 正方向 小 大 x=3 不是 是 不是 能使不等式成立的未知数 的值，叫做不等式的解。 新知导入 下列各数中，那些是不等式 的解？52 x -3, -2, -1, 0, 1.5, 2.5, 3, 3.5, 5, 7 不等式 x+2>5 ，除了上面提到的解之外，你还可以说出它的那些 解? 解有（ ）个无数 新知讲解 我们发现，-3、-2、-1、0、1.5、2.5、3都不是不等式x+2 >5 的解，而3.5、5、7都是不等式x+2>5的解.由此可以看出，不 等式x +2>5有许多个解.进而看出，大于3的每一个数都不是 不等式x + 2 > 5的解，而不大于3的每一个数都是不等式 x + 2> 5的解.不等式x +2>5 解有无数个，它们组成一个集合， 称为不等式x+ 2>5的解集. 新知讲解 一个不等式的所有解，组成这个不等式的解的集合， 简称为这个不等式的解集(solution set). 不等式的解集必须满足两个条件： 第一，解集中的任何一个数值都能使不等式成立； 第二，解集外的任何一个数值都不能使不等式成立，不等式的解可以有 无数个，而其解集只有一个． 注意 1、判断下列说法是否正确，并说明理由． (1) x＝3是不等式 3x ≥ 9的解集； (2)不等式 3x ≥ 9的解是 x＝3； (3) x＝3是不等式 3x ≥ 9的一个解； (4) x ≥3是不等式 3x ≥ 9的解； (5)不等式 3x ≥ 9的解集是 x ≥ 3. 课堂练习 × × √ √ × 2、下列说法中，正确的是(　　) A. x＝－3是不等式x＋4＜1的解 B. x＞ 是不等式－2x＞－3的解集 C．不等式x＞－5的负整数解有无数多个 D．不等式x＜7的非正整数解有无数多个 课堂练习 3 2 D 不等式的解集是指满足这个不等式的未知数的所有的值，故不等 式的所有解组成了解集，解集中包括每一个解． 不等式的解与不等式的解集有什么不同？ 新知讲解 新知讲解 研究不等式的一个重要任务,就是求出不等式的解集。求不等 式的解集的过程，叫做解不等式。 不等式x + 2 > 5的解集，可以表示成x > 3，它也可以在数轴上直 观地表示出来，如图 1 所示. -2 -1 0 1 2 3 4 5 6 图1 -2 -1 0 1 2 3 4 5 6 图2 同样，如果某个不等式的解集为x ≤ -2，也可以在数轴上直观地表示 出来，如图 2 所示 新知讲解 这里，出现了符号“≤”. 一般地，解集x ≤ a，表示“x小于或等于a” ，或者说“x不大于a”. 类似地，解集x ≥ a，表示“x大于或等于a”，或者说 “x不小于a”.在数轴上，解集x ≤ a，是指表示数 a 的点左边的部分，包括表 示数 a 的点在内，这一点画成实心圆点.而解集x < a，则是指表示数 a 的点 左边的部分，但不包括表示数 a 的点，这一点画成空心圆圈. 对于解集x ≥ a 和x > a在数轴上的表示，与此相仿. 新知讲解 1. 不等式的解集的表示方法有两种： (1)用不等式表示；(2)用数轴表示． 2. 不等式的解集在数轴上的表示方法有以下几种： 不等式的解集 数轴表示 注意 x＞a 端点用空心圆圈，方向向 右 x＜a 端点用空心圆圈，方向向 左 x ≥ a 端点用实心圆点，方向向 右 x ≤ a 端点用实心圆点，方向向 左 新知讲解 例 在数轴上表示下列不等式， 6)1( x 2)2( x -2 -1 0 1 2 3 4 5 6 （1） （2） -2 -1 0 1 2 3 4 5 6 课堂练习 3、将数轴上表示的对应不等式连起来。 0)1( x 4)2( x 2)3( x 5)4( x -2 -1 0 1 2 3 4 5 6 -2 -1 0 1 2 3 4 5 6 -2 -1 0 1 2 3 4 5 6 -2 -1 0 1 2 3 4 5 6 课堂练习 4、在数轴上表示出下列不等式 50)1(  x 62)2(  x -2 -1 0 1 2 3 4 5 6 -2 -1 0 1 2 3 4 5 6 （1） （2） （0，1，2，3，4） （-1，0，1，2，3，4，5，6） (1)在定方向时，要注意不要搞错方向，大于向右．小于向左． (2)有等于号(≤，≥)画实心圆点，无等于号(<，>)画空心圆圈． (3)在数轴上表示不等式的解集，一般分三步：画数轴，定界点， 定方向. 新知讲解 拓展提高 (1)在数轴上表示不等式的解集时，要确定边界和方向： ① 边界：有等号的是实心圆点，无等号的是空心圆圈； ② 方向：大于向右，小于向左． (2)在用数轴表示不等式的解集时，端点用实心圆点和用空心圆圈 表示的含义不同，要特别注意． 课堂总结 知识总结 知识方法要点 关键总结 注意事项 不等式的解 能使不等式成立的未知数的值 指未知数的某个值 不等式的解集 一个含未知数的不等式的所有解 解集中包含了每一个不等式的 解 不等式解集的表示方法 ①用简单的不等式表示；②用数轴 表示 界点和方向 方法规律总结 (1)一般地，一个不等式的解不止一个，往往有多个，甚至有无数个；(2)不等式的解集包括不等 式的每一个解，是所有解的集合，解集包括解；(3)用数轴表示不等式的解集时，应确定两点： 一是确定“界点”，二是确定“方向”．若解集包含“界点”，则用实心圆点，否则用空心圆 圈．对于方向，相对于界点而言，大于向孝画，小于向左画. 作业布置 谢谢