北师大版数学七上综合练习（三） 8页

重庆八中初 2020 级七年级上练习（三） 试题卷（A）（满分 100 分） 班级： 学号： 姓名： 成绩：_________ 一、选择题（每小题 4 分,共 40 分） 1． 3- 的相反数是（ ） A． 3 1- B． 3 1 C． 3 D． 3- 2．有四包真空小包装辣条，每包以标准克数（120 克）为基准，超过的克数记作正数，不足的克 数记作负数，以下数据是记录结果，其中表示实际克数最接近标准克数的是（ ） A． 2 B． 3 C． 3 D． 4 3．下列计算正确的是（ ） A． 32 6 B． 24 16   C． 8 8 0   D． 5 2 3    4．在有理数 2( 1) ， 3( )2   ， 2  ， 3( 2) 中负数有（ ）个 A． 4 B． 3 C． 2 D． 1 5．若 x x  ，则 x 一定是 （ ） A．负数 B．正数 C． 0 D． 负数或 0 ． 6．右图是一数值转换机，若输入的 x 为 5 ，则输出的结果为（ ） A． 21 B． 11 C． －9 D． －17 7．实数 ,a b 在数轴上的位置如图所示，则下列式子错误的是（ ） A． 0a b  B． a b C． 1a b   D． a b a b   8． 2017 个不全相等的有理数之和为零，则这 2017 个有理数中（ ） A．至少有一个是零 B．至少有 1008 个是正数 C．至少有一个是负数 D．至多有 2015 个是负数 9．某商店出售一种商品，下列四个方案中，最后价格最低的方案是（ ） A．先提价 30%，再降价 30% B．先提价 20%，再降价 20% C．先降价 20%，再提价 30% D．先降价 20%，再提价 20% 10．如图所示，将一张长方形的纸对折 1 次，可得到 1 条折痕，继续对折，对折时每次折痕与上 次的折痕保持平行，对折 2 次可得到 3 条折痕，对折 3 次可得到 7 条折痕，如果对折 6 次， 输 出 ×(－3) 输入 x －2 可得到折痕（ ） A．31 B．32 C．63 D．64 二．填空题（每小题 4 分,共 20 分） 11．成渝高铁是“十二五”国家重点铁路建设项目，2010 年 3 月开工建设，2015 年 12 月 26 日开通 运营．该工程估算投资总额 3980000 万元，将数 3980000 用科学计数法表示为 ． 12． 1 12.5 ( 2 ) 1.75 ( )4 2      = ． 13．若 3x  ， 2y  ，且 x y ，则 x y  ． 14．若 4a   ，且 a b  ，则 b= ． 15． x 是最大负整数， y 是最小的正整数，则代数式 23 3 2 yx  的值为 ． 三、解答题（共 40 分） 16．计算：（每小题 4 分，共 24 分） （1） 3( 2 ) ( 0.6)5    （2） 61）-（+43+9）-（ （3） 230042 17- . （4） ）12 7-6 5 9 4-（136）-（  （5）4 3 221 0.25 ( 2) 4 ( ) 13            （6） ）15-（19 189  17. （6 分）已知 22)( x 与 2y 互为相反数，求 xyyx  的值. 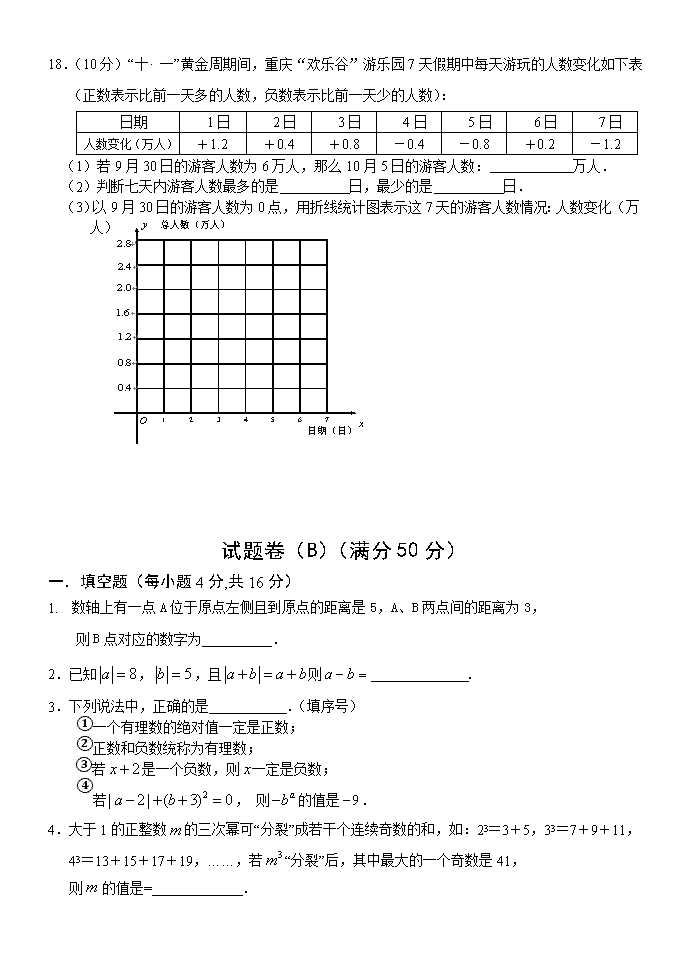18．（10 分）“十· 一”黄金周期间，重庆“欢乐谷”游乐园 7 天假期中每天游玩的人数变化如下表 （正数表示比前一天多的人数，负数表示比前一天少的人数）： 日期 1 日 2 日 3 日 4 日 5 日 6 日 7 日 人数变化（万人） ＋1.2 ＋0.4 ＋0.8 －0.4 －0.8 ＋0.2 －1.2 （1）若 9 月 30 日的游客人数为 6 万人，那么 10 月 5 日的游客人数： 万人． （2）判断七天内游客人数最多的是 日，最少的是 日． （3）以 9 月 30 日的游客人数为 0 点，用折线统计图表示这 7 天的游客人数情况：人数变化（万 人） 试题卷（B）（满分 50 分） 一．填空题（每小题 4 分,共 16 分） 1. 数轴上有一点 A 位于原点左侧且到原点的距离是 5，A、B 两点间的距离为 3， 则 B 点对应的数字为__________． 2．已知 8a  ， 5b  ，且 a b a b   则 a b  . 3．下列说法中，正确的是 ．（填序号） ①一个有理数的绝对值一定是正数； ②正数和负数统称为有理数； ③若 2x  是一个负数，则 x 一定是负数； ④若 2| 2| ( 3) 0a b    ， 则 ab 的值是 9 ． 4．大于 1 的正整数 m 的三次幂可“分裂”成若干个连续奇数的和，如：23＝3＋5，33＝7＋9＋11， 43＝13＋15＋17＋19，……，若 3m “分裂”后，其中最大的一个奇数是 41， 则 m 的值是= ___ ． 总人数（万人） 日期（日） 二、解答题（共 34 分） 5．计算：（每小题 4 分，共 16 分） （1） 11 [2 ( 3)] 5 5       （2） 6）2 3-3-3 1（）15-（  （3）  2016 7 8 1 1 11 12 168 7 3 4 6               （4） ）5 2-6 1 10 1-3 2（）30 1-（  6．（6 分）对于有理数 ba, ，定义新运算： ba baba 3 3   ．如果 1 3 2 0x y xz      ， 求 )( zyx  的值． 7．（12 分）已知 2017321 xxxx ,,,,  都是不等于 0 的有理数，请探究以下问题： （1） 1 1 1 x xy  ，则 1y _____． （2） 21 21 2 2 1 1 2 xx xx x x x xy   ，则 2y （3） 321 321 3 3 2 2 1 1 3 xxx xxx x x x x x xy   ，则 3y _____ __ ___． （4）由以上探究可以知道： 2017 2017 3 3 2 2 1 1 2017 x x x x x x x xy  ，共有_____ __ ___种不同的 值，在 2017y 这些不同的值中，最大值与最小值的差值等于___ __ ___， 2017y 的这些不同 的值的绝对值的和等于____ __ ___． 重庆八中初 2020 级七年级上定时练习（三） （A 卷）答题卷 班级：_________ 学号：_________ 姓名：_________ 成绩：_________ 一、选择题（每小题 4 分，共 40 分） 题号 1 2 3 4 5 6 7 8 9 10 答案 二、填空题（每小题 4 分，共 20 分） 11、________ 12、 __ 13、________ 14、________ 15、___________ 三、解答题（共 40 分） 16．计算：（每小题 4 分，共 24 分） （（1） 3( 2 ) ( 0.6)5    （2） 61）-（+43+9）-（ （3） 230042 17- . （4） ）12 7-6 5 9 4-（136）-（  （5）4 3 221 0.25 ( 2) 4 ( ) 13            （6） ）15-（19 189  17. （6 分）已知 22)( x 与 2y 互为相反数，求 xyyx  的值. 18．（10 分）“十· 一”黄金周期间，重庆“欢乐谷”游乐园 7 天假期中每天游玩的人数变化如下表 （正数表示比前一天多的人数，负数表示比前一天少的人数）： 日期 1 日 2 日 3 日 4 日 5 日 6 日 7 日 人数变化（万人） ＋1.2 ＋0.4 ＋0.8 －0.4 －0.8 ＋0.2 －1.2 （1）若 9 月 30 日的游客人数为 6 万人，那么 10 月 5 日的游客人数： 万人． （2）判断七天内游客人数最多的是 日，最少的是 日． （3）以 9 月 30 日的游客人数为 0 点，用折线统计图表示这 7 天的游客人数情况：人数变化（万 人） 总人数（万人） 日期（日） 答题卷（B）（满分 50 分） 一．填空题（每小题 4 分,共 16 分） 1、________ 2、 __ 3、________ 4、________ 二、解答题（共 34 分） 5．计算：（每小题 4 分，共 16 分） （1） 11 [2 ( 3)] 5 5       （2） 6）2 3-3-3 1（）15-（  （3）  2016 7 8 1 1 11 12 168 7 3 4 6               （4） ）5 2-6 1 10 1-3 2（）30 1-（  6．（6 分）对于有理数 ba, ，定义新运算： ba baba 3 3   ．如果 1 3 2 0x y xz      ， 求 )( zyx  的值． 7．（12 分）已知 2017321 xxxx ,,,,  都是不等于 0 的有理数，请探究以下问题： （1） 1 1 1 x xy  ，则 1y _____． （2） 21 21 2 2 1 1 2 xx xx x x x xy   ，则 2y （3） 321 321 3 3 2 2 1 1 3 xxx xxx x x x x x xy   ，则 3y _____ __ ___． （4）由以上探究可以知道： 2017 2017 3 3 2 2 1 1 2017 x x x x x x x xy  ，共有_____ __ ___种不同的 值，在 2017y 这些不同的值中，最大值与最小值的差值等于___ __ ___， 2017y 的这些不同 的值的绝对值的和等于____ __ ___．