人教版七年级上册数学第一章有理数有理数的加法法则教学课件 23页

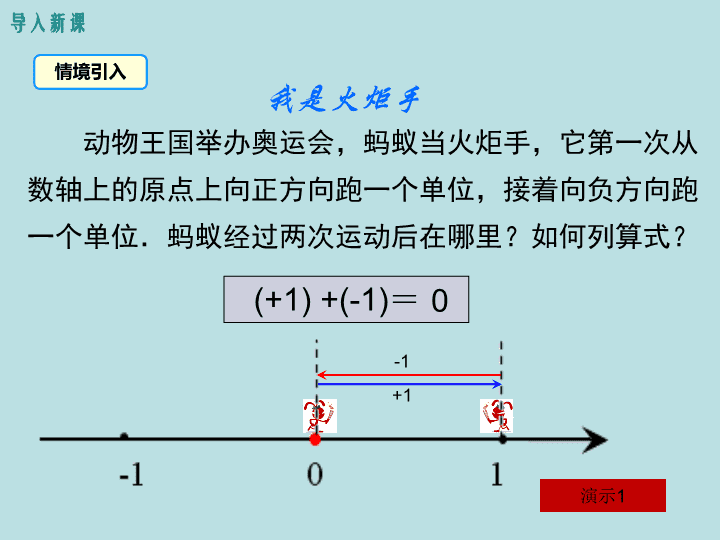
第一章 有理数 人教版 七年级数学上册 1.3.1 有理数的加法 有理数的加法法则 我是火炬手 演示1 +1 -1 (+1) +(-1)＝ 0 动物王国举办奥运会，蚂蚁当火炬手，它第一次从 数轴上的原点上向正方向跑一个单位，接着向负方向跑 一个单位．蚂蚁经过两次运动后在哪里？如何列算式？ 导入新课 情境引入 讲授新课 有理数的加法法则一 合作探究 一只可爱的小狗，在一条东西走向的笔直 公路上行走，现规定向东为正，向西为负. 0 1 2 3 4-1-2-3 东 如果小狗先向东行走2米，再继续向东行走1 米，则小狗两次一共向哪个方向行走了多少米？ 0 1 2 3 4-1-2-3 东 解：小狗一共向东行走了（2+1）米，写成 算是为： （+2）+（+1）= +（2+1）（米） 想一想 如果小狗先向西行走2米，再继续向西行走1 米，则小狗两次一共向哪个方向行走了多少米？ 0 1 2 3 4-1-2-3 东 想一想 解：两次行走后，小狗向西走了（2+1）米.用算 式表示： （- 2）+（- 1）= -（2 + 1）（米） （+2）+（+1）= +（2+1）=+3 （-2）+（-1）= -（2+1）=-3 加数 加数 和 你从上面两个式子中发现了什么？ 比一比 同号两数相加，取相同的符号，并把绝对值相加. 有理数加法法则一： (1) 如果小狗先向西行走3米，再继续向东行走 2米，则小狗两次一共向哪个方向行走了多少米？ 0 1 2 3 4-1-3 -2 东 小狗两次一共向西走了（3-2）米.用算式表 示为： -3+（+2）=-（3-2）（米） 想一想 (2) 如果小狗先向西行走2米，再继续向东行走 3米，则小狗两次一共向哪个方向行走了多少米？ 0 1 2 3 4-1-2 东 小狗两次一共向东走了（3-2）米.用算式表 示为： -2+（+3）=+（3-2）（米） （3） 如果小狗先向西行走2米，再继续向东行 走2米，则小狗两次一共向哪个方向行走了多少米？ 0 1 2 3 4-1-2 东 （-2）+（+2）= 0（米） 解：小狗一共行走了0米.写成算式为： -2 + (+3) = +（3-2） -3 + (+2）= -（3-2） -2 + (+2）= （2-2） 比一比 加数 加数 和 加 数 异 号 加数的绝对 值不相等 你从上面三个式子中发现了什么？ 有理数加法法则二： 异号两数相加，绝对值相等时和为0；绝对值 不相等时，取绝对值较大的加数的符号，并 用较大的绝对值减去较小的绝对值. 如果小狗先向西行走3米，然后在原地休息， 则小狗向哪个方向行走了多少米？ 0 1 2 3 4-1-2 东 小狗向西行走了3米.写成算式为： （-3）+0= -3（米） 想一想 有理数加法法则三： 一个数同0相加，仍得这个数. 有理数加法法则 (1)同号两数相加，结果取相同符号，并把绝对值 相加． (2)异号两数相加，结果取绝对值较大的加数的符 号，并将较大的绝对值减较小的绝对值．互为相反 数的两个数相加得0． (3)一个数同0相加，仍得这个数． 总结归纳 例1 计算： （1）（－4）＋（－8）；（2）（－5）＋13； （3）0＋（－7）； （4）（－4.7）＋4.7． 典例精析 解：（1）（－4）＋（－8） 　　　 　＝－（4＋8） 　　　　 ＝－12 （2）（－5）＋13＝＋（13－5）＝8 （3）0＋（－7）＝－7 （4）（－4.7）＋3.9＝－（4.7-3.9）＝-0.8 通过有理数加法法则的学习，同学们，你们认为 如何进行有理数加法运算呢？ 方法总结：1.先判断类型（同号、异号等）； 2.再确定和的符号； 3.最后进行绝对值的加减运算. 议一议 例2 已知│a│= 8，│b│= 2； （1）当a、b同号时，求a+b的值； （2）当a、b异号时，求a+b的值. 分析：先根据的a、b符号，分类讨论，再计算a+b的值 解：因为│a│= 8，│b│= 2，所以a= ±8，b= ±2. （1）因为a、b同号，所以a= 8，b= 2或a= -8，b= -2. 所以a+b= 8+2=10，或a+b=- 8+（-2）=-10. （2）因为a、b异号，所以a= 8，b=- 2或a= -8，b= 2. 所以a+b= 8+（-2）=6，或a+b=- 8+2=-6. 若|x－3|与|y＋2|互为相反数，求x＋y的值． 变式训练 解：由题意得|x－3|+|y＋2|=0，又|x－3|≥0，|y＋ 2|≥0，所以x－3= 0，y＋2=0，所以x=3 ，y=－2. 所以x＋y=3－2=1. 红队 黄队 蓝队 净胜球 红队 4:1 0:1 2 黄队 1:4 1:0 －2 蓝队 1:0 0:1 0 例3 足球循环赛中，红队胜黄队4:1，黄队胜 蓝队1:0，蓝队胜红队1:0，计算各队的净胜球数. 分析： 有理数加法的应用二 解：每个队的进球总数记为正数，失球总数记 为负数，这两数的和为这队的净胜球数. 三场比赛中，红队共进4球，失2球，净胜 球数为（＋4）＋（－2）＝＋（4－2）＝2 黄队共进2球，失4球，净胜球为 （＋2）＋（－4）＝－（4－2）＝－2 篮球共进（ ）球，失（ ）球， 净胜球数为（ ）. 1 1 （＋1）＋（－1）＝0 海平面的高度为0m.一艘潜艇从海平 面先下潜40m,再上升15m.求现在这艘 潜艇相对于海平面的位置.（上升为 正，下潜为负） 解：潜水艇下潜40m,记作-40m;上升 15m,记作+15m.根据题意，得 （-40）+（+15）=-（40-25）=-25（m) 答：现在这艘潜艇位于海平面下25m处. -50m -30m -20m 海平面 -10m 0m -40m 针对训练 当堂练习 1.两个有理数的和为零，则这两个有理数一定 （ ） A.都是零 B.至少有一个是零 C.一正一负 D.互为相反数 2.在1，－1，-2这三个数中，任意两数之和的最 大值是（ ） A.1 B.0 C.-1 D.3 D B A. a+c＜0 B. b+c＜0 C. -b+a＜0 D.-a+b+c＜0 3.已知有理数a,b,c在数轴上的位置如图所示，则 下列结论中错误的是（ ） A.1 B.－5 C.－5或－1 D.5或1 4.若│x│= 3，│y│= 2，且x>y，则x+y的值为（ ） C D (1)(-0.6)+(-2.7)； (2)3.7+(-8.4)； (3)3.22+1.78； (4)7+(-3.3). 5.计算 答案：(1)-3.3 (2)-4.7 (3)5 (4)3.7