青岛初中数学七年级下册11 同底数幂的乘法 17页

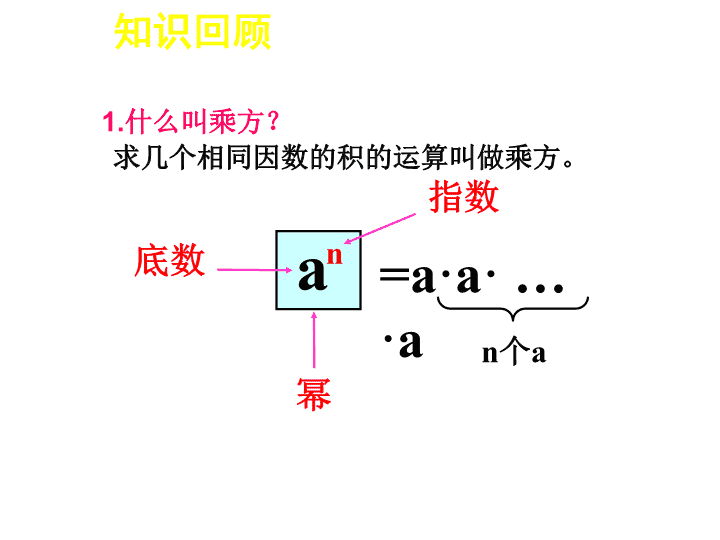
11.1 同底数幂的乘法 一种电子计算机每秒可进行1014次运算，它工作103秒可 进行多少次运算？ 问题情景 列式：1014×103 怎样计算 1014×103呢？ an 指数 幂 = a·a· … ·an个a 底数 1.什么叫乘方？ 求几个相同因数的积的运算叫做乘方。 知识回顾 练一练 : （1） 25表示什么？ （2） 10×10×10×10×10 可以写成 什么形式? 25 = . 2×2×2×2×2 105 10×10×10×10×10 = . (乘方的意义） (乘方的意义） 知识回顾 v 式子103×102中的两个因数有何特点？ 底数相同 5 （2×2×2）×（2×2） 5 a3×a2 = = a （ ） . 5（a a a）（a a） =2×2×2×2×2 = a a a a a 3个a 2个a 5个a 请同学们先根据自己的理解，解答下列各题. 103 ×102 =（10×10×10）×（10×10） = 10（ ） ； 23 ×22 = = 2（ ） ； 探究新知 我们把底数相同的幂称为同底数幂 请同学们观察下面各题左右两边，底数、指数有什么关 系？ 103 ×102 = 10（ ） 23 ×22 = 2（ ） a3× a2 = a（ ） 5 5 5 猜想: am · an= ? (当m、n都是正整数) 　　分组讨论，并尝试证明你的猜想是否正确. 3+2 3+2 3+2 = 10 （ ）； = 2 （ ）； = a （ ） 。 观察讨 论 猜想: am · an= (m、n都是正整数) am · an = m个a n个a = aa…a = a m + n （乘方的意义） (m+n)个a 由此可得同底数幂的乘法性质： am · an = am+n (m、n都是正整数) （aa…a）（aa…a） am+n 猜想证明 （乘方的意义） （乘法结合律） · am · an = am+n (当m、 n都是正整数)同底数幂相乘， 想一想： 当三个或三个以上同底数幂相乘时，是否也 　 具有这一性质呢？ 怎样用公式表示？ 底数　　，指数　　。不变 相加 同底数幂的乘法性质： 　请你尝试用文字概 括这个结论。 我们可以直接利 用它进行计算. 如 43×45=43+ 5 =48 如 am·an·ap = am+n +p （m、n、p都是正整数） 幂的底数必须相同， 相乘时指数才能相加. Ø 练习 Ø 计算：（抢答） (1011 ) ( a10 ) （ x10 ） （ b6 ） （2） a7 ·a3 （3） x5 ·x5 （4） b5 · b （1） 105×106 （5）10×102×104 （107） （6） y4·y3·y2·y (y10) 例1 计算： （1）（－3）7×（ －3）6； （2）（ ）3 × ；─ 10 1 ─ 10 1 （3） －x3 • x5； 例题分析： （4） b2m • b2m+1. 解：－x3 • x5 =－x3+5= －x8； 解：b2m • b2m+1 = b2m+2m+1 = b4m +1. 下面的计算对不对？如果不对，怎样改正？ （1）b5 · b5= 2b5 （ ） （2）b5 + b5 = b10 （ ） （3）x5 ·x5 = x25 ( ) （4）-y6 · y5 = -y11 ( ) （5）c · c3 = c3 ( ) （6）m3 + m3 = 2m3 ( ) b5 · b5= b10 b5 + b5 = 2b5 x5 · 10 c · c3 = c4 × × √ × √ × 辨一辨 (1) -y · (-y)2 · y3 (2) (x+y)3 · (x+y)4 例2.计算: 解:原式= - y · y2 · y3 解: (x+y)3 · (x+y)4 = am · an = am+n 公式中的a可代表 一个数、字母、式 子等。 =(x+y)7 拓展延伸 = -y1+2+3=- y6 (x+y)3+4 练习 ： （1） － a3 · a6 ； （2）x · (-x) 4·x 3 解：（1） 原式 = －a3 + 6 （4）原式 = x3m +2m—1 （3）(x-y)2· (y-x)3 (4) x3m · x2m—1（m为正整 数） = x5m—1 = (y-x)5 =－a9 练一练 2 3 = x9（2）原式 = x · x ·x = x2+4+342 （3）原式 =(y-x) · (y-x) = (y-x)2+32 3 同底数幂相乘，　 底数　　 指数　 am · an = am+n (m、n正 整数) 小结 我学到了 什么？ 知识　 方法　　　 　“特殊→一般→特 殊” 　 例子 公式 应用 不变， 相加. 1.底数不同时，要先化成同底数幂才能运用法 则;底数可以是一个数，也可以是单项式或多项 式. 3.解题时，要注意指数为1的情况，不要漏掉. 2.解题时，底数是负数（分数）的要用括号把底 数括起 来. 注意事项 课后作业： 1.课本78页习题 2.填空： （1） 8 = 2x，则 x = ； （2） x4 · = x9。 我思，我进步 结束寄语 只有不断的思考,才 会有新的发现;只有量的 变化,才会有质的进步.祝 大家学有所得! 下课了!