北京课改版数学七上《点、线、面、体》同步练习 3页

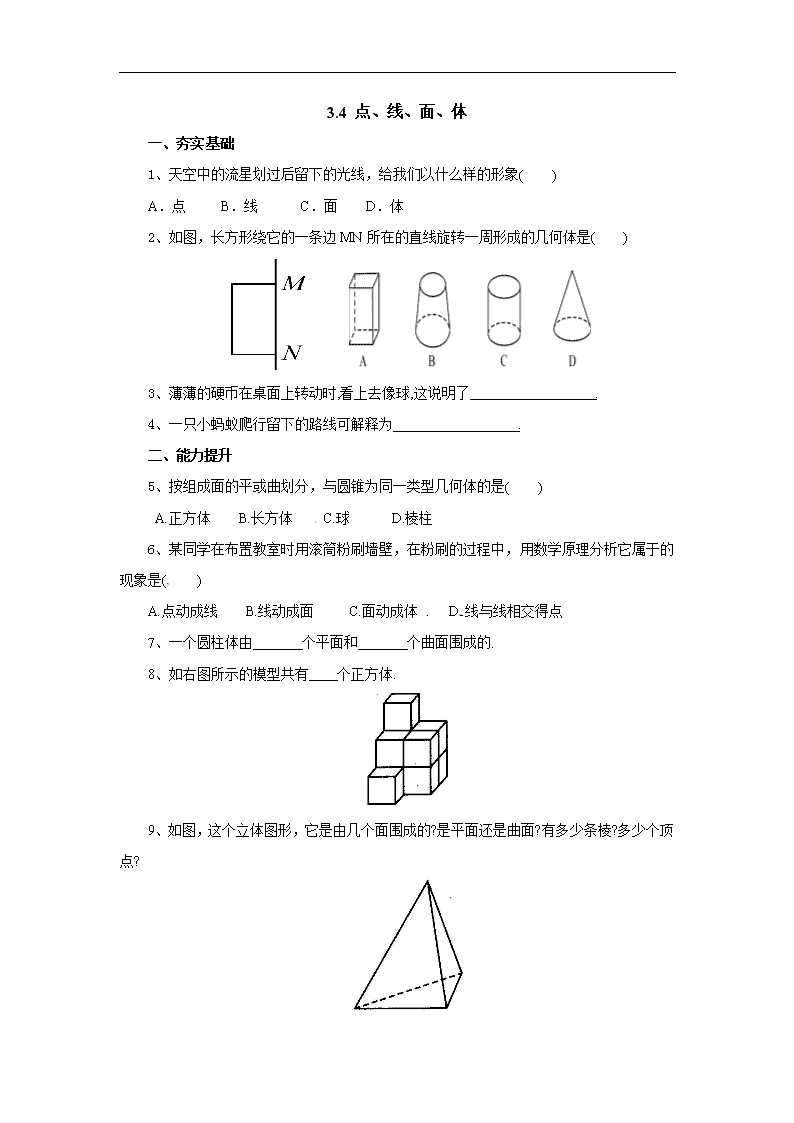
3.4 点、线、面、体 一、夯实基础 1、天空中的流星划过后留下的光线，给我们以什么样的形象( ) A．点 B．线 C．面 D．体 2、如图，长方形绕它的一条边 MN 所在的直线旋转一周形成的几何体是( ) 3、薄薄的硬币在桌面上转动时,看上去像球,这说明了 . 4、一只小蚂蚁爬行留下的路线可解释为 . 二、能力提升 5、按组成面的平或曲划分，与圆锥为同一类型几何体的是( ) A.正方体 B.长方体 C.球 D.棱柱 6、某同学在布置教室时用滚筒粉刷墙壁，在粉刷的过程中，用数学原理分析它属于的 现象是( ) A.点动成线 B.线动成面 C.面动成体 D .线与线相交得点 7、一个圆柱体由 个平面和 个曲面围成的. 8、如右图所示的模型共有 个正方体. 9、如图，这个立体图形，它是由几个面围成的?是平面还是曲面?有多少条棱?多少个顶 点? 答： 10、我们知道用 5 根火柴可以拼成 2 个正三角形.那么，再增加一根火柴棒，你能否拼 出 4 个正三角形呢?怎样拼?请你说明它是平面图形还是立体图形? 答： 三、课外拓展 11、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存 在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题: (1)根据上面多面体模型,完成表格中的空格: 多面体 顶点数(V) 面数(F) 棱数(E) 四面体 4 4 长方体 8 6 12 正八面体 8[ 12 正十二面体 20 12 30 你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 . (2)一个多面体的面数比顶点数大 8,且有 30 条棱 ,则这个多面体的面数是 . (3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接 而成,且有 24 个顶点,每个顶点处都有 3 条棱,设该多面体外表三角形的个数为 x 个,八边形的 个数为 y 个,求 x+y 的值. 答： 四、中考链接 12、(丽水市)下列图形中，属于立体图形的是（ ） A． B． C． D． 参考答案 夯实基础 1、C 2、C 3、面动成体 4、点动成线 能力提升 5、C 6、B 7、2 1 8、10 9、由 4 个面围成，都是平面，有 6 条棱，4 个顶点. 10、能，如图所示： 是立体图形. 课外拓展 11、解:(1)四面体的棱数为 6;正八面体的顶点数为 6;关系式为 V+F-E=2. (2)由题意得,F-8+F-30=2, 解得 F=20. (3)因为有 24 个顶点,每个顶点处都有 3 条棱,两点确定一条直线,所以共有 24×3÷2=36 条 棱.那么 24+F-36=2,解得 F=14,所以 x+y=14. 中考链接 12、C