初中数学7年级教案：第5讲 相交线 8页

辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 ‎ 时 间 A / B / C / D / E / F段 主 题 相交线 教学内容 ‎1．理解对顶角、互为邻补角的概念，掌握对顶角的性质．‎ ‎2．能依据对顶角的性质、邻补角的概念等知识，进行简单的计算．‎ ‎3．理解两条直线垂直的概念，掌握垂线的性质，能过一点作已知直线的垂线．‎ ‎（以提问的形式回顾）‎ 小练习：‎ 一、相交线 ‎1．如果两个角相等，那么这两个角是对顶角． ( )‎ ‎2．如果两个角有公共顶点且没有公共边，那么这两个角是对顶角． ( )‎ ‎3．有一条公共边的两个角是邻补角． ( )‎ ‎4．如果两个角是邻补角，那么它们一定互为补角． ( )‎ ‎5．对顶角的角平分线在同一直线上． ( )‎ ‎6．有一条公共边和公共顶点，且互为补角的两个角是邻补角． ( )‎ ‎7．如图，直线AB、CD相交于O点，∠AOE＝90°．‎ ‎(1)∠1和∠2叫做______角；∠1和∠4互为______角；‎ ‎∠2和∠3互为_______角；∠1和∠3互为______角；‎ ‎∠2和∠4互为______角．‎ ‎(2)若∠1＝20°，那么∠2＝______；‎ ‎∠3＝∠BOE－∠______＝______°－______°＝______°；‎ ‎∠4＝∠______－∠1＝______°－______°＝______°．‎ 答案：1．×；2．×；3．×；4．√；5．√；6．×；‎ 二、垂线 ‎1．垂线的性质 性质1：平面内，过一点____________与已知直线垂直．‎ 性质2：连接直线外一点与直线上各点的_________中，_________最短．‎ ‎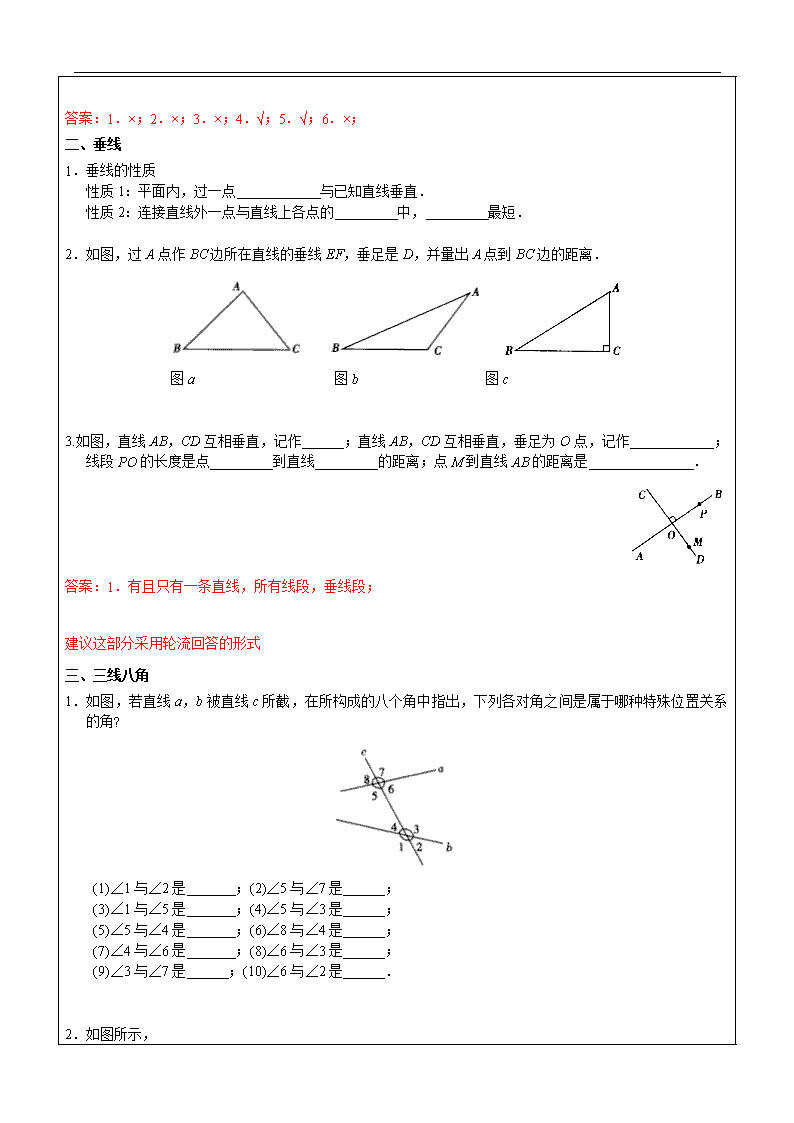2．如图，过A点作BC边所在直线的垂线EF，垂足是D，并量出A点到BC边的距离．‎ ‎ ‎ 图a 图b 图c ‎3.如图，直线AB，CD互相垂直，记作______；直线AB，CD互相垂直，垂足为O点，记作____________；线段PO的长度是点_________到直线_________的距离；点M到直线AB的距离是_______________．‎ 答案：1．有且只有一条直线，所有线段，垂线段；‎ 建议这部分采用轮流回答的形式 三、三线八角 ‎1．如图，若直线a，b被直线c所截，在所构成的八个角中指出，下列各对角之间是属于哪种特殊位置关系的角?‎ ‎(1)∠1与∠2是_______；(2)∠5与∠7是______；‎ ‎(3)∠1与∠5是_______；(4)∠5与∠3是______；‎ ‎(5)∠5与∠4是_______；(6)∠8与∠4是______；‎ ‎(7)∠4与∠6是_______；(8)∠6与∠3是______；‎ ‎(9)∠3与∠7是______；(10)∠6与∠2是______．‎ ‎2．如图所示，‎ ‎(1)∠AED和∠ABC可看成是直线______、______被直线______所截得的_______角；‎ ‎(2)∠EDB和∠DBC可看成是直线______、______被直线_______所截得的______角；‎ ‎(3)∠EDC和∠C可看成是直线_______、______被直线______所截得的______角．‎ 答案： 2．(1)ED，BC，AB，同位；(2)ED，BC，BD，内错；(3)ED，BC，AC，同旁内．‎ ‎“三线八角”归纳总结 角的名称 位置特征 基本图形 图形结构特征 同位角 在两条被截直线同旁，在截线同侧 形如字母“F”‎ ‎（或倒置）‎ 内错角 在两条被截直线之内，在截线两侧 形如字母“Z”‎ 同旁内角 在两条被截直线之内，在截线同侧 形如字母“U”‎ ‎（采用教师引导，学生轮流回答的形式）‎ 例1：回答下列问题：‎ ‎(1)三条直线AB，CD，EF两两相交，图形中共有几对对顶角(平角除外)?几对邻补角?‎ ‎(2)四条直线AB，CD，EF，GH两两相交，图形中共有几对对顶角(平角除外)?几对邻补角?‎ 答案：(1)有6对对顶角，12对邻补角．(2)有12对对顶角，24对邻补角．‎ 例2：已知：如图，直线AB，CD相交于点O，OE平分∠BOD，OF平分∠COB，∠AOD∶∠DOE＝4∶1．求∠AOF的度数．‎ 答案：提示：设∠DOE＝x°，由∠AOB＝∠AOD＋∠DOB＝6x＝180°，可得x＝30°，∠AOF＝4x＝120°．‎ 试一试：已知：如图，三条直线AB，CD，EF相交于O，且CD⊥EF，∠AOE＝70°，若OG平分∠BOF．求∠DOG．‎ 答案：55°．‎ 例3：如图，已知∠AOB及点P，分别画出点P到射线OA、OB的垂线段PM及PN．‎ ‎ ‎ 图a 图b 图c 例4：如图，三条直线两两相交，共有几对对顶角?几对邻补角?几对同位角?几对内错角?几对同旁内角?‎ 答案：6对对顶角，12对邻补角，12对同位角，6对内错角，6对同旁内角．‎ 试一试：如图，直线AB，CD与直线EF，GH分别相交，图中的同旁内角共有( )．‎ ‎(A)4对 (B)8对 ‎(C)12对 (D)16对 答案：D ‎（学生统一完成，互相批改，教师针对重难点详细讲解）‎ 1. 经过两点可以画 条直线。两条直线相交，有 个交点；‎ 2. ‎“互为邻补角”包括两个角之间的 关系和 关系，而“互为补角”仅指两个角之间的 关系；‎ 3. 如果两条直线的夹角为锐角，那么就说这两条直线互相 ，其中的一条直线叫做另一条直线的 ；‎ 4. 如果两条直线的夹角为直角，那么就说这两条直线互相 ，其中的一条直线叫做另一条直线的 ，它们的交点叫做 ； ‎ 5. 过一点有 条直线与已知直线垂直；‎ 6. 联结直线外一点与直线上各点的所有线段中， 最短； ‎ 7. 直线外一点到这条直线的垂线段的长度，叫做 ，特别地，如果一个点在直线上，那么就说这个点到这条直线的距离为 ；‎ 8. 如图1：∠1的邻补角是______；∠1的对顶角是_______ ‎ 9. 如图2：三条直线相交于点O，∠AOD的对顶角是______∠AOC的邻补角是______‎ ‎ ‎ 图1 图2 图3‎ ‎10．如图1：∠2－∠1＝50°，则∠4＝________这两条直线的夹角是_______度。‎ ‎11．如图3：直线AB，CD相交于点O，OA平分∠COE，∠COE＝70°，则∠BOD的＝_______‎ ‎12．如图4：三条直线相交于点O，∠AOF＝ 120°，∠BOD＝90°；那么∠BOF＝____ _，∠EOC＝ ___________，直线AB，CD的夹角等于_________‎ ‎14．如图5：∠1＝60° ，∠2＝30°；那么直线AC，BC的夹角是______________‎ 图4 图5‎ ‎15．如图5：线段AD的长是点__________到直线_________________的距离。线段BD的长是点__________到直线_________________的距离。线段CD的长是点__________到直线_________________的距离。‎ ‎ ‎ ‎ ‎ 答案：1、一、一； 2、位置、数量、数量； 3、斜交、斜线； 4、垂直，垂线，垂足； ‎ ‎5、有且只有一条； 6、垂线段； 7、点到直线的距离，零； 8、∠2和∠4，∠3； ‎ ‎9、∠BOC，∠BOC 和∠AOD； 10、115°，65°；11、35°；12、60°，30°，90°；‎ ‎14、30； 15、A，BC；B，AD；C，AD； ‎ ‎ ‎ 本节课主要知识点：相交线所成角的概念（对顶角，邻补角，三线八角）‎ ‎【巩固练习】‎ ‎1．已知：如图，直线a，b，c两两相交，∠1＝2∠3，∠2＝86°．则∠4的度数为 ．‎ ‎2．如图：x＝_________________；y＝___________________‎ ‎3.如图，∠1和∠2是内错角，可看成是由直线( )．‎ ‎(A)AD，BC被AC所截构成 ‎(B)AB，CD被AC所截构成 ‎(C)AB，CD被AD所截构成 ‎(D)AB，CD被BC所截构成 ‎4.分析一下图中的同位角，同旁内角，内错角。‎ 答案：∠4＝43°；32°，84°；B；‎ 同位角：∠1与∠B，∠4与∠C，∠2与∠A，∠3与∠A 内错角：∠1与∠3，∠2与∠4‎ 同旁内角：∠A与∠1，∠A与∠4，∠2与∠B，∠3与∠C，∠1与∠4，∠2与∠3，‎ ‎∠C与∠B，∠A与∠B，∠A与∠C。‎ ‎【预习思考】‎ ‎1. 在同一平面内，两条不重合的直线位置关系：‎ ‎2. 平行线基本性质： ‎ ‎3. 平行线判定方法：‎ ‎4. 平行线的传递性：‎