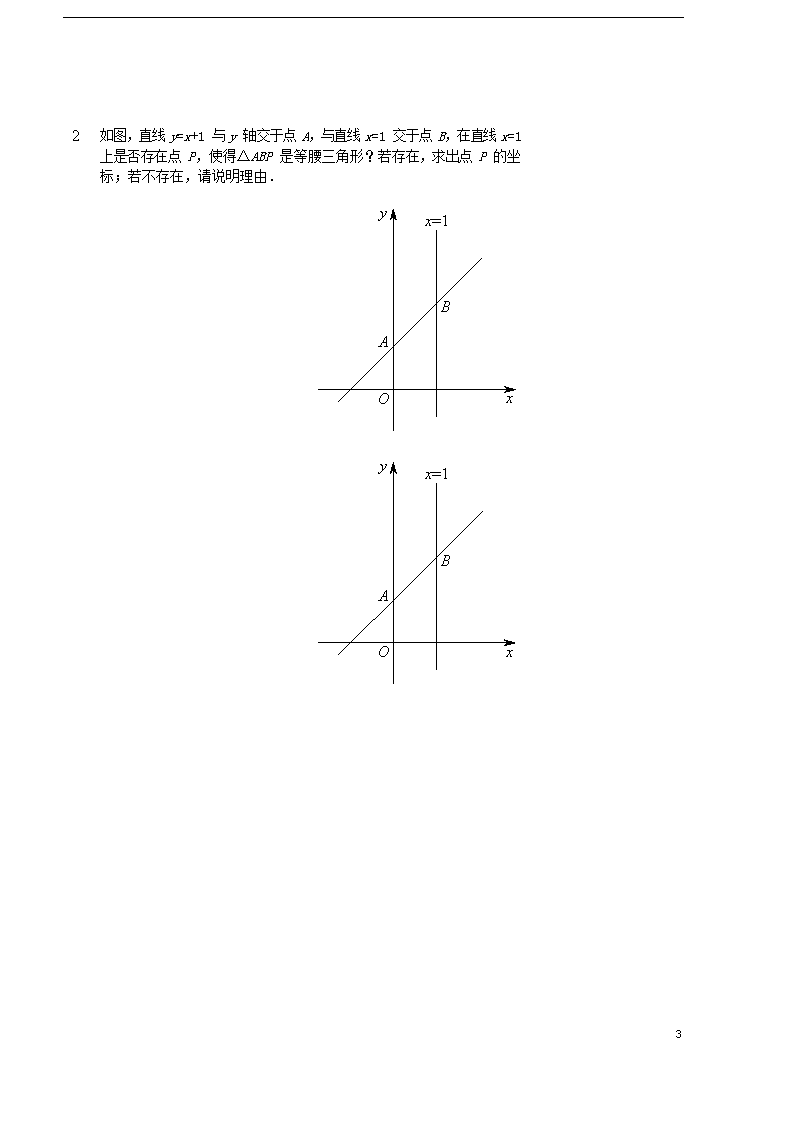2020学年七年级数学上册 一次函数之存在性问题（一）习题 （新版）鲁教版 6页

一次函数之存在性问题（一）（习题）‎ Ø 例题示范 y B D A E O x 例 1：如图，将 Rt△AOB 放入平面直角坐标系中，点 O 与坐标原 ‎3‎ 点重合，点 A 在 x 轴负半轴上，点 B 在 y 轴正半轴上，且 OB= 2 ，‎ ‎∠BAO=30°．将△AOB 沿过点 B 的直线折叠，使点 O 落在 AB 边上的点 D 处，折痕交 x 轴于点 E．‎ ‎（1）求直线 BE 的解析式．‎ ‎（2）求点 D 的坐标．‎ P y ‎4‎ ‎3‎ D B ‎2 3‎ A ‎30°‎ E 2 O x ‎6‎ P y B D F P1‎ P3‎ A P4 P2 E O x ‎（3）x 轴上是否存在点 P，使得△PAD 是等腰三角形？若存在， 求出点 P 的坐标；若不存在，请说明理由．‎ 图1‎ 6‎ 思路分析：‎ ‎1．研究背景图形（如图 1）‎ ‎2．分析不变特征，确定分类标准 ‎P(？，0)‎ ‎△PAD 等腰定 ：A，D 动：P 定线段 AD ‎‎ 腰 两圆 底 一线 6‎ ‎3．分析特殊状态的形成因素， ‎ 画出符合题意的图形并 ‎ 6‎ 以 P4 为例：‎ ‎①P4 是怎么来的 ‎3‎ 6‎ ‎（分析形成因素，垂直平分）‎ ‎②垂直平分怎么用 ‎y = - ‎0‎ ‎3x - 4‎ 6‎ x = -4 ? 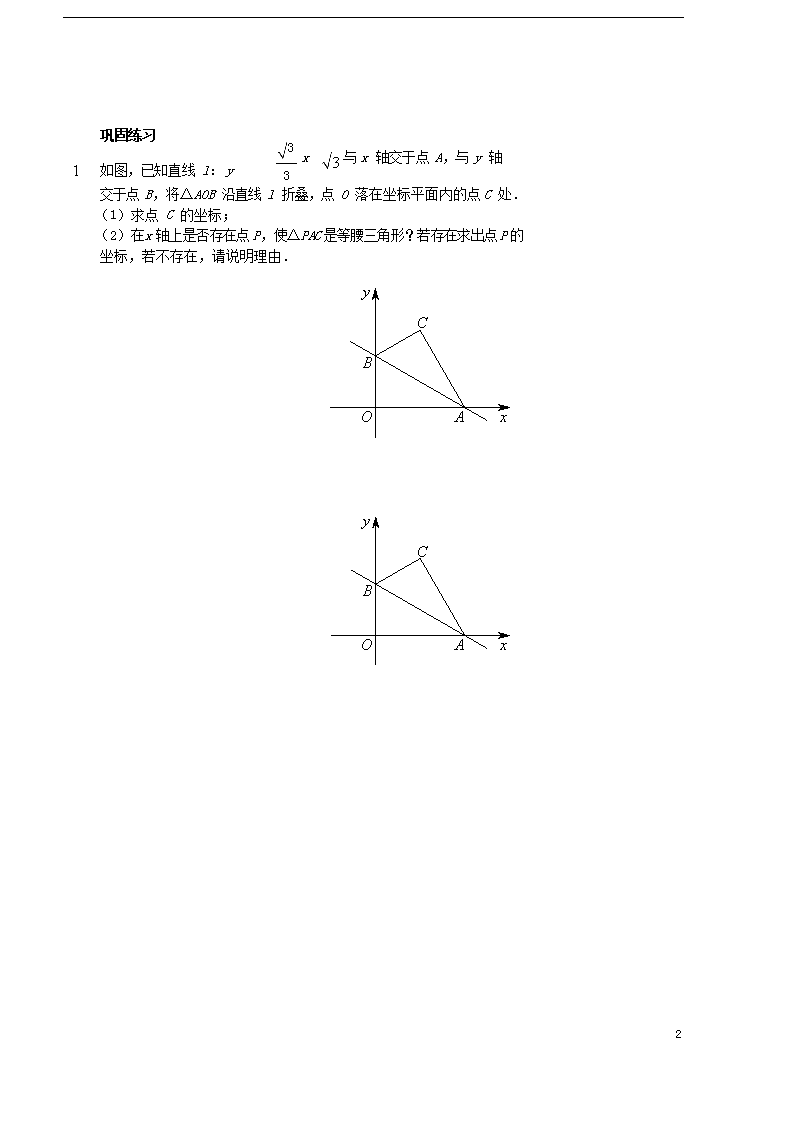P4 (-4，0)‎ 6‎ 6‎ Ø 巩固练习 1. 如图，已知直线 l： y = - ‎‎ ‎3 x + 与 x 轴交于点 A，与 y 轴 ‎3‎ ‎3‎ 6‎ 交于点 B，将△AOB 沿直线 l 折叠，点 O 落在坐标平面内的点 C 处．‎ ‎（1）求点 C 的坐标；‎ ‎（2）在 x 轴上是否存在点 P，使△PAC 是等腰三角形？若存在求出点 P 的坐标，若不存在，请说明理由．‎ y C B O A x y C B O A x 6‎ 1. 如图，直线 y=x+1 与 y 轴交于点 A，与直线 x=1 交于点 B，在直线 x=1 上是否存在点 P，使得△ABP 是等腰三角形？若存在，求出点 P 的坐标；若不存在，请说明理由．‎ y x=1‎ B A O x y x=1‎ B A O x 6‎ 1. 如图，直线 y = - 1 x +1与 x 轴、y 轴分别交于点 A，B，以线 ‎2‎ 段 AB 为直角边在第一象限内作等腰 Rt△ABC，∠BAC=90°，‎ 若在第二象限内有一点 P(a， 1 )，且△ABP 的面积与△ABC ‎2‎ 的面积相等，则 a 的值为 ．‎ y B C P O A x 2. 如图，在平面直角坐标系中，函数 y=2x+12 的图象分别交 x 轴、y 轴于 A，B 两点，过点 A 的直线交 y 轴正半轴于点 M， 且点 M 为线段 OB 的中点．若点 P 是直线 AM 上一点，使得S△ABP=S△AOB，则点 P 的坐标为 ．‎ y B M A O x 6‎ 6‎ 1. 如图，直线 y = - ‎3 x + 与 x 轴、y 轴分别交于点 A，B，‎ ‎3‎ ‎3‎ 6‎ 点 C 的坐标为(3，2 3) ，P 为直线 x=1 上的动点，且△ABP的面积与△ABC 的面积相等．‎ ‎（1）求△ABC 的面积；‎ ‎（2）求点 P 的坐标．‎ y x=1‎ C B O A x 6‎ 6‎