2020学年七年级数学上册 一次函数与几何综合（二）讲义 （新版）鲁教版 6页

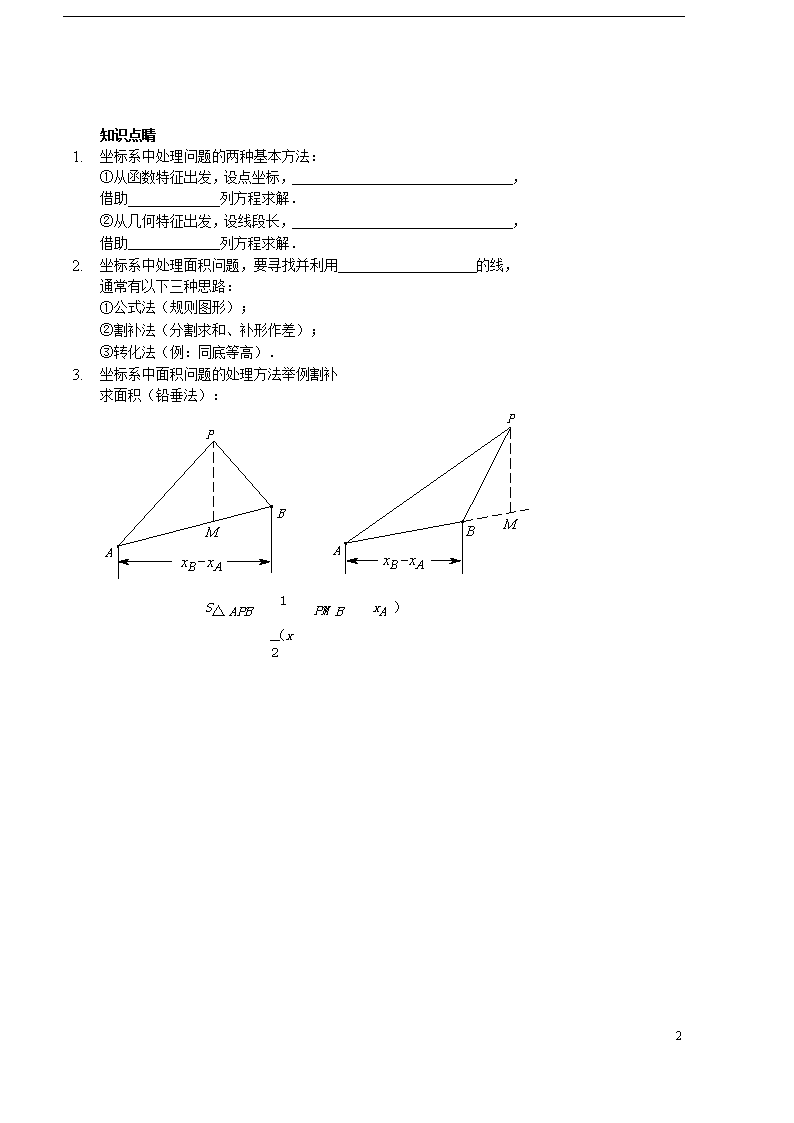
一次函数与几何综合（二）（讲义）‎ Ø 课前预习 1. 如图，在平面直角坐标系 xOy 中，已知 A(1，2)，B(3，5)，‎ C(6，3)，求△ABC 的面积．‎ y B A C O x 2. 用铅笔做讲义第 1，2 题，并将计算、演草保留在讲义上，先看知识点睛，再做题，思路受阻时（某个点做了 2~3 分钟） 重复上述动作，若仍无法解决，课堂重点听．‎ 3. 6‎ Ø 知识点睛 1. 坐标系中处理问题的两种基本方法：‎ ‎①从函数特征出发，设点坐标， ， 借助 列方程求解．‎ ‎②从几何特征出发，设线段长， ， 借助 列方程求解．‎ 2. 坐标系中处理面积问题，要寻找并利用 的线，通常有以下三种思路：‎ ‎①公式法（规则图形）；‎ ‎②割补法（分割求和、补形作差）；‎ ‎③转化法（例：同底等高）．‎ 3. 坐标系中面积问题的处理方法举例割补求面积（铅垂法）：‎ P B M xB -xA M xB -xA P B A A 6‎ S△ APB ‎= 1 × PM × (x ‎2‎ ‎‎ B - xA )‎ 6‎ Ø 精讲精练 1. 如图，点 A 在直线 l1：y=3x 上，且点 A 在第一象限，过点 A 作 AB⊥x 轴，交直线 l2：y=x 于点 B．若 AB=3，则点 A 的坐标是 ．‎ y l1‎ A l2‎ B O x y ‎1‎ y=- 2 x+b B y=x E M C O D A x 第 1 题图 第 2 题图 2. 如图，已知函数 y = - 1 x + b 的图象与 x 轴、y 轴分别交于点 A，‎ ‎2‎ B，与函数 y=x 的图象交于点 M，点 M 的横坐标为 2，点 C 为线段 AM 上一点，过点 C 作 x 轴的垂线，垂足为点 D，交函数 y=x 的图象于点 E．若 ED=4CD，则点 E 的坐标为 ‎ ．‎ 3. 如图，在平面直角坐标系中，直线 OM 经过点 A(6，6)，过 A 作正方形 ABCD，在直线 OA 上有一点 E，过 E 作正方形 EFGH．已知正方形的边长与坐标轴平行，直线 OC 经过点 G， 且正方形 ABCD 的边长为 2，正方形 EFGH 的边长为 3，则点 F 的坐标为 ．‎ y M E H A D F C G B O x 6‎ 1. 如图，在平面直角坐标系中，点 A，C 和 B，D 分别在直线 y = 1 x + 3 和 x 轴上，若△OAB，△BCD 都是等腰直角三角形，‎ ‎2‎ 则点 C 的坐标为 ． y C A O B D x 2. 如图，在平面直角坐标系中，已知 A(2，3)，B(4，2)，则△AOB y A O x B 的面积为 _．‎ y A B O x 第 5 题图 第 6 题图 3. 如图，A，B 是直线 y = kx + 7 上的两点，点 A 的坐标为(-1，‎ ‎4‎ ‎3)，点 B 的横坐标为 3，则△AOB 的面积为 ．‎ y P B A O C x D 4. 如图，直线 y=-x+4 与 x 轴、y 轴分别交于点 A，B，点 P 的坐标为(-2，2)，则 S△PAB= ．‎ y B P O A x 第7题图 第8题图 5. 如图，直线 AB：y=x+1 与 x 轴、y 轴分别交于点 A，B，直线CD：y=kx-2 与 x 轴、y 轴分别交于点 C，D，直线 AB 与直线 CD 交于点 P．若 S△APD=4.5，则 k 的值为 ．‎ 6‎ 1. 如图，在平面直角坐标系中，已知 A(2，4)，B(6，6)，‎ C(8，2)，则四边形OABC的面积为 ．‎ y B A C O x 2. 如图，已知直线 l1，l2 相交于点 A(2，1)，点 B(8，4)在 l1 上，‎ l2 的表达式为 y=2x-3．C 为 l2 上的一个动点，且在点 A 的右侧，若△ABC 的面积为 9，求点 C 的坐标．‎ y l2‎ C l1‎ B A O x 3. 如图，直线 l1：y=x 与直线 l2：y=-2x+3 相交于点 A，点 B 在直线 l1 上，且横坐标为 4．C 为 l2 上的一个动点，且在点 A 的左侧，若△ABC 的面积为 9，则点 C 的坐标为 ．‎ l2 y C l1‎ B A O x 6‎ ‎【参考答案】‎ Ø 课前预习 ‎1. 13‎ ‎2‎ Ø 知识点睛 1. ‎①坐标转线段长，几何特征 ‎②线段长转坐标，函数特征 2. 横平竖直 Ø 精讲精练 ‎，‎ ‎1. ( 3 9 )‎ ‎2 2‎ ‎2. (4，4)‎ ‎3. (9，6)‎ ‎4. (30，18)‎ ‎5. 4‎ ‎6. 7‎ ‎2‎ ‎7. 8‎ ‎8. 5‎ ‎2‎ ‎9. 24‎ ‎10. C(4，5)‎ ‎11. (-1，5)‎ 6‎