七年级数学下册第一章整式的乘除4整式的乘法第2课时单项式与多项式相乘教学课件（新版）北师大版 17页

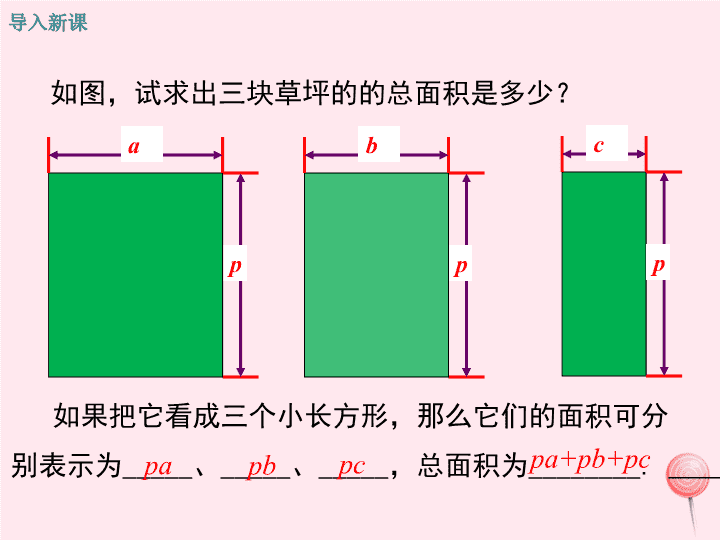
1.4 整式的乘法 第一章 整式的乘除 导入新课 讲授新课 当堂练习 课堂小结 第2课时 单项式与多项式相乘 学习目标 1.能根据乘法分配律和单项式与单项式相乘的法则， 探究单项式与多项式相乘的法则； 2.掌握单项式与多项式相乘的法则并会运用.（重点， 难点） 如图，试求出三块草坪的的总面积是多少？ 如果把它看成三个小长方形，那么它们的面积可分 别表示为_____、_____、_____，总面积为________. pp a b p c pa pcpb 导入新课 pa+pb+pc pp a b p c 如果把三个小长方形拼成一个大长方形，那么它 们总面积可以表示为___________. p（a+b+c） pa+pb+pcp(a+b+c) p (a + b+ c) pb + pcpa + 根据乘法的分配律 试一试 单项式与多项式相乘 讲授新课 方法总结：根据乘法分配律,乘以它的每一项． 知识要点 单项式乘以多项式的法则 单项式与多项式相乘，将单项式分别乘以多项式 的每一项，再将所得的积相加. （1）依据是乘法分配律； （2）积的项数与多项式的项数相同. 注意 p b p a p c 典例精析 例1 计算： （1）2ab(5ab2+3a2b)； （2）( －2ab)·2 3 2 ab ; 2 1 ab （3）5m2n(2n+3m－n2)； （4）2(x+y2z+xy2z3)·xyz； 解：(1)原式=2ab·5ab2+2ab·3a2b =10a2b3+6a3b2； (2)原式= 2 3 2 ab )2( 2 1 abab  ab 2 1  ; 3 1 2232 baba  (3)原式=5m2n·2n+5m2n·3m+5m2n·(－n2) =10m2n2+15m3n－5m2n3; (4)原式=(2x+2y2z+2xy2z3)·xyz =2x2yz+2xy3z2+2x2y3z4. 例2 一条防洪堤坝，其横断面是梯形，上底宽a米， 下底宽(a＋2b)米，坝高 a米． (1)求防洪堤坝的横断面面积； 2 1 解：(1) [a＋(a＋2b)]× a ＝ a(2a＋2b) ＝ a2＋ ab(平方米)． 故防洪堤坝的横断面面积为( a2＋ ab)平方米； 2 1 2 1 4 1 2 1 2 1 2 1 2 1 (2)如果防洪堤坝长100米，那么这段防洪堤坝的体 积是多少立方米？ (2)( a2＋ ab)×100＝50a2＋50ab(立方米)． 故这段防洪堤坝的体积为50a2＋50ab(立方米)． 2 1 2 1 例3 先化简，再求值：5a(2a2－5a＋3)－2a2(5a＋5) ＋7a2，其中a＝2. 解：5a(2a2－5a＋3)－2a2(5a＋5)＋7a2＝10a3－25a2 ＋15a－10a3－10a2＋7a2＝－28a2＋15a， 当a＝2时，原式＝－82. 方法总结：在计算时要注意先化简然后再代值计算． 整式的加减运算实际上就是去括号与合并同类项． 当堂练习 1.单项式与多项式相乘，就是用单项式去乘多项式的 ________,再把所得的积________. 2.4（a-b+1)=_____________. 每一项 相加 4a-4b+4 3.3x（2x-y2)=____________.6x2-3xy2 4.（2x-5y+6z)(-3x)=________________.-6x2+15xy-18xz 5.(-2a2)2（-a-2b+c)=_________________.-4a5-8a4b+4a4c 6.计算： （1）(－4x)·(2x2+3x－1)； ＝-8x3-12x2+4x; 解：原式＝(－4x)·(2x2)+(－4x)·3x+(－4x)·(－1) (2)( ab2－2ab)· ab.3 2 2 1 解：原式＝ ab2· ab－2ab· ab ＝ a2b3－a2b2. 3 2 2 1 2 1 3 1 7.计算：－2x2·(xy+y2)-5x(x2y-xy2). （1）将2x2与5x前面的“-”看成性质符号； （2）单项式与多项式相乘的结果中，应将同类项合并. 注意 解：原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2) =-2x3y+(-2x2y2)+(-5x3y)+5x2y2 =-7x3y+3x2y2. 8.先化简，再求值3a(2a2-4a+3)-2a2(3a+4)，其中 a=-2. 解：3a(2a2-4a+3)-2a2(3a+4) =6a3-12a2+9a-6a3-8a2 =-20a2+9a. 当a=-2时，原式=-20×(－2)2+9×(－2)=-98. 住宅用地 人民广场 商业用地 3a 3a+2b 2a-b 4a 9.如图，一块长方形地用来建造住宅、广场、商厦， 求这块地的面积. 解：4a[(3a+2b)+(2a－b)] ＝4a(5a+b) ＝4a·5a+4a·b =20a2+4ab. 答：这块地的面积为 20a2+4ab. 课堂小结 整式的 乘法 单项式乘 多 项 式 实质上是转化为单项式×单项式 注 意 （1）计算时,要注意符号问题,多项式中每一项都 包括它前面的符号,单项式分别与多项式的每 一项相乘时，同号相乘得正，异号相乘得负 （2）不要出现漏乘现象 （3）运算要有顺序：先乘方，再乘除，最后加减 （4）对于混合运算，注意最后应合并同类项