上海教育版数学七下《全等三角形》同步练习2 6页

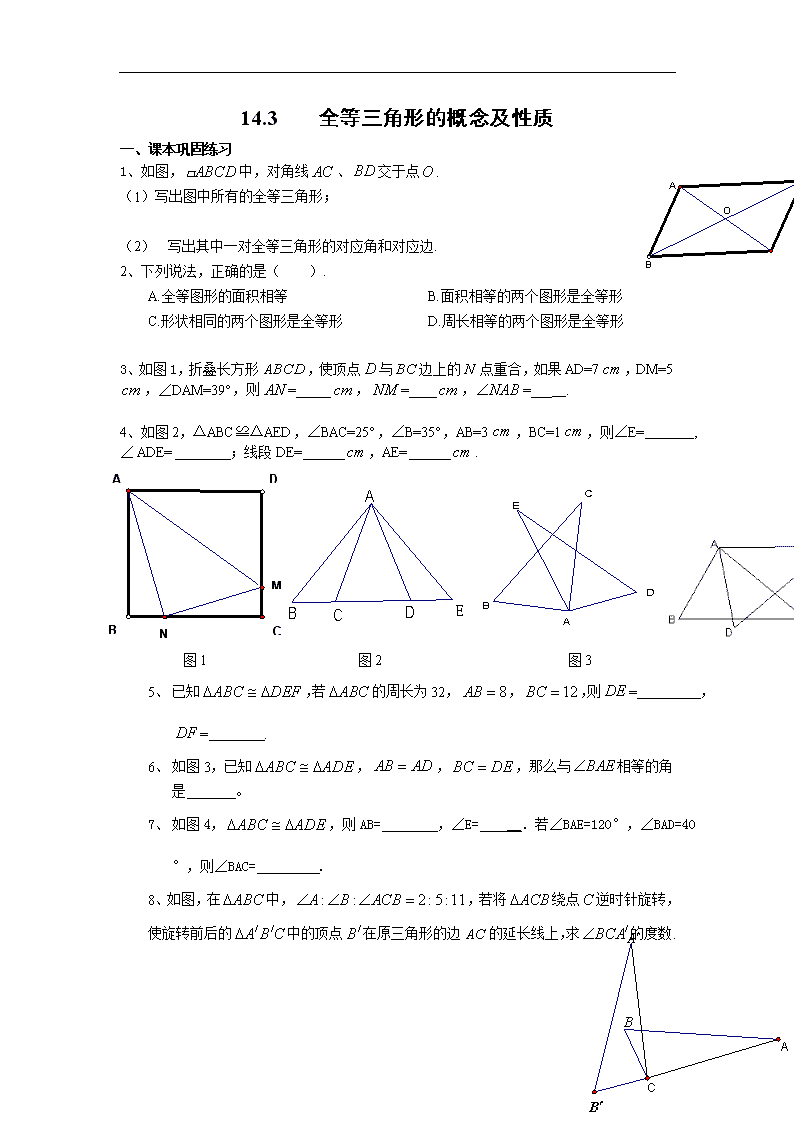
14.3 全等三角形的概念及性质 一、课本巩固练习 1、如图， ABCD 中，对角线 AC 、 BD 交于点O . （1）写出图中所有的全等三角形； （2） 写出其中一对全等三角形的对应角和对应边. 2、下列说法，正确的是（ ）. A.全等图形的面积相等 B.面积相等的两个图形是全等形 C.形状相同的两个图形是全等形 D.周长相等的两个图形是全等形 3、如图 1，折叠长方形 ABCD ，使顶点 D 与 BC 边上的 N 点重合，如果 AD=7 cm ， DM=5 cm ，∠DAM=39°，则 AN =_____ cm ， NM =____ cm ， NAB =___ . 4、如图 2，△ABC≌△AED，∠BAC=25°，∠B=35°，AB=3 cm ，BC=1 cm ，则∠E= , ∠ ADE= ；线段 DE= cm ，AE= cm . 图 1 图 2 图 3 5、 已 知 ABC DEF   ， 若 ABC 的 周 长 为 32 ， 8AB  ， 12BC  ， 则 DE = ， DF = . 6、 如图 3，已知 ABC ADE   ， AB AD ， BC DE ，那么与 BAE 相等的角 是 。 7、 如图 4， ABC ADE   ，则 AB= ，∠E= __．若∠BAE=120°，∠ BAD=40°，则∠BAC= . 8、如图，在 ABC 中， : : 2:5:11A B ACB    ，若将 ACB 绕点C 逆时针旋转， 使旋转前后的 / /A B C 中的顶点 /B 在原三角形的边 AC 的延长线上，求 /BCA 的度 数. 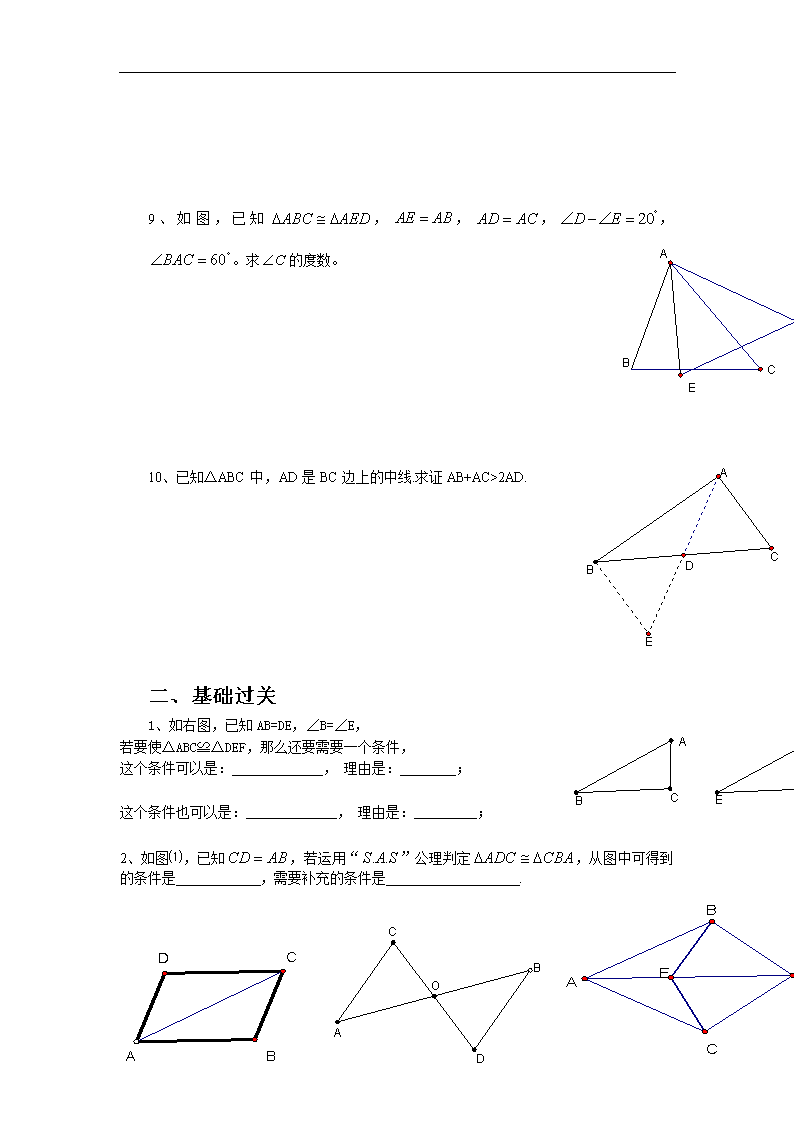M DA NB C 图4 E D C B A 图 4 O D BC A Ｅ D C B A C A 9 、 如 图 ， 已 知 ABC AED   ， AE AB ， AD AC ， 20D E     ， 60BAC   。求 C 的度数。 10、已知△ABC 中，AD 是 BC 边上的中线.求证 AB+AC>2AD. 二、基础过关 1、如右图，已知 AB=DE，∠B=∠E， 若要使△ABC≌△DEF，那么还要需要一个条件， 这个条件可以是：_____________， 理由是：________； 这个条件也可以是：_____________， 理由是：_________； 2、如图⑴，已知 CD AB ，若运用“ . .S A S ”公理判定 ADC CBA   ，从图中可得到 的条件是 ，需要补充的条件是 . B E D C A D B E A C E C D B A E A D C B F D C AB O B C D A ⑴ ⑵ ⑶ 3、如图⑵，已知 AB 与CD 相交于点O ， / /AC BD ，如果需要 AOC BOD   ，则还应 增加的条件 或 或 . 4、 如图⑶，已知 AB AC ，BD CD ，F在 AD 上，那么图中共有 对全等三角形。 5、下列语句正确的是（ ） A．有一边对应相等的两个直角三角形必全等 B.两个等边三角形必全等 C.有一边对应相等的两个等腰直角三角形必全等 D.顶角、底边分别相等的两个等 腰三角形必全等 5、 在 ARt△B C 的斜边 BC 上截取 CD CA ，过点 D 作 DE BC 交 AB 于 E ，则有 （ ） A． DE DB B. DE AE C. AE BE D. AE BD 6、 如图， BE 、CD 、 AF 相交与 F , B C   , AFE AFD   . 求证： DF EF . 7、 如图， AB AC ， AD AE ， EAD BAC   .求证：△ABD≌△ACE A B C D E A F C B E D E C A B D 8、如图 6，已知 AB=DE，AF=DC，BE=CF，求证：∠A=∠D. 9、如图，已知点 E 在 AC 上， 1 2   ， 3 4   ，说明 BE DE 的理 由. 10、点 P 是正方形 ABCD 内一点，在正方形外有一点 E ，满足 BE BP ，AE CP .求证： （1） ABE CBP   ；（2） PBE 是直角. 11、如图，在等边 ABC 的 AC、BC 边上各取一点 E、F，使 AE=CF，AF、BE 交于点 O， 请你说理由： （1） ABE CAF   ；(2) ∠ABE=∠CAF；（3） 60BOF   . A D B E F C图 6 2 1 3 4 E D C B A P E D C B A O C A B E F 12、求证三角形的一边的两断点到这两边的中线或中线的延长线的距离相等. 13、如图,在△ABC 中, M 在 BC 上, D 在 AM 上, AB AC , DB DC .问 BM CM 吗?说明理由. 14、如图, △ABC, AD 是它的角平分线,且 BD CD , ED 、 DF 分别垂直于 AB 、 AC ， 垂足为 E 、 F ，请说明 BE CF . 15、如图，△ABC 是等边三角形，点 D、E、F 分别是线段 AB、BC、CA 上的点。 E F D A B C C M A B D F E B D A C （1）若 AD=BE=CF，问△DEF 是等边三角形吗？试证明你的结论； （2）若△DEF 是等边三角形，问 AD=BE=CF 成立吗？试证明你的结论．