八年级数学上册第七章平行线的证明5三角形的内角和定理第1课时三角形内角和定理的证明课件 北师大版 16页

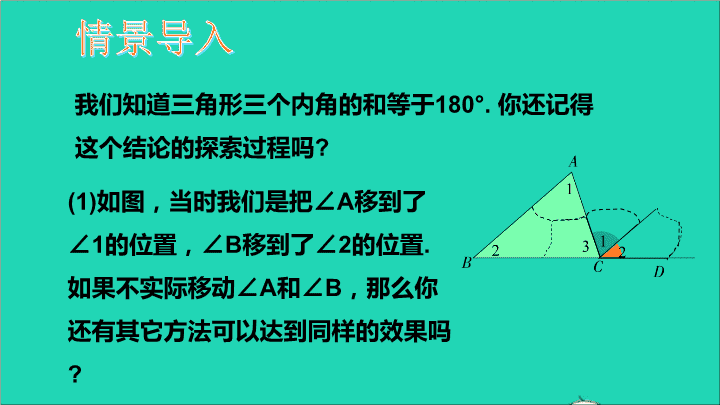
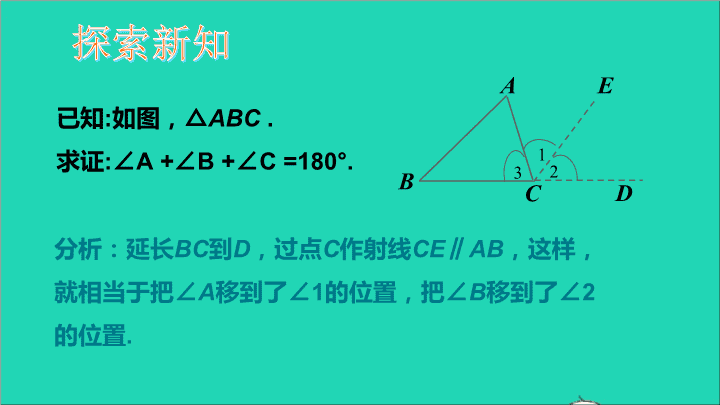
第1课时三角形内角和定理的证明 情景导入我们知道三角形三个内角的和等于180°.你还记得这个结论的探索过程吗?(1)如图，当时我们是把∠A移到了∠1的位置，∠B移到了∠2的位置.如果不实际移动∠A和∠B，那么你还有其它方法可以达到同样的效果吗? 已知:如图，△ABC.求证:∠A+∠B+∠C=180°.ABCE分析：延长BC到D，过点C作射线CE∥AB，这样，就相当于把∠A移到了∠1的位置，把∠B移到了∠2的位置.探索新知213D 证明：作BC的延长线CD，过点C作CE∥AB，则你还有其它方法来证明三角形内角和定理吗?∠1=∠A(两直线平行，内错角相等),∠2=∠B(两直线平行，同位角相等).又∵∠1+∠2+∠3=180°(平角的定义),∴∠A+∠B+∠ACB=180°(等量代换). ABC△ABC中，∠A+∠B+∠C=180°.三角形内角和定理三角形内角和定理三角形三个内角的和等于180°. 想一想在证明三角形内角和定理时，小明的想法是把三个角“凑”到A处，他过点A作直线PQ∥BC(如图)，他的想法可以吗?ABCPQ ABC3证明：过点A作PQ∥BC，则∠1=∠B(两直线平行,内错角相等),∠2=∠C(两直线平行,内错角相等),又∵∠1+∠2+∠3=180°(平角的定义),∴∠BAC+∠B+∠C=180°(等量代换).PQ12 例如图，在△ABC中，∠B=38°,∠C=62°,AD是△ABC的角平分线，求∠ADB的度数. 随堂练习1.直角三角形的两锐角之和是多少度？证明你的结论. 2.正三角形的一个内角是多少度？证明你的结论. 3.已知：如图，在△ABC中，∠A=60°，∠C=70°，点D，E分别在AB和AC上，且DE//BC.求证：∠ADE=50°.ABCDE 1.在△ABC中，∠A=80°,∠B-∠C=40°，则∠C=.2.∠A=∠B+∠C，则这个三角形是.3.直角三角形两锐角的平分线相交所成的角的度数为（）A.45°B.135°C.45°或135°D.都不对巩固练习30°直角三角形C 4.若△ABC的一个内角是另一个内角的，也是第三个内角的，则它的三个内角的度数为（）A.30°，60°，90°B.40°，60°，80°C.48°，52°，80°D.48°，72°，60°D 5.如图，AD、AE分别为△ABC的高线和角平分线，且∠B=35°，∠C=45°，求∠DAE的度数.解：∵∠B=35°，∠C=45°且∠B+∠C+∠BAC=180°∴∠BAC=100°∵AE平分∠BAC∴∠BAE=50°∵AD⊥BC∴∠ADB=90°∵∠B+∠ADB+∠BAD=180°∴∠BAD=55°∴∠DAE=∠BAD-∠BAE