北师大版八年级数学上册 第七章 平行线的证明 单元测试卷（有答案） 17页

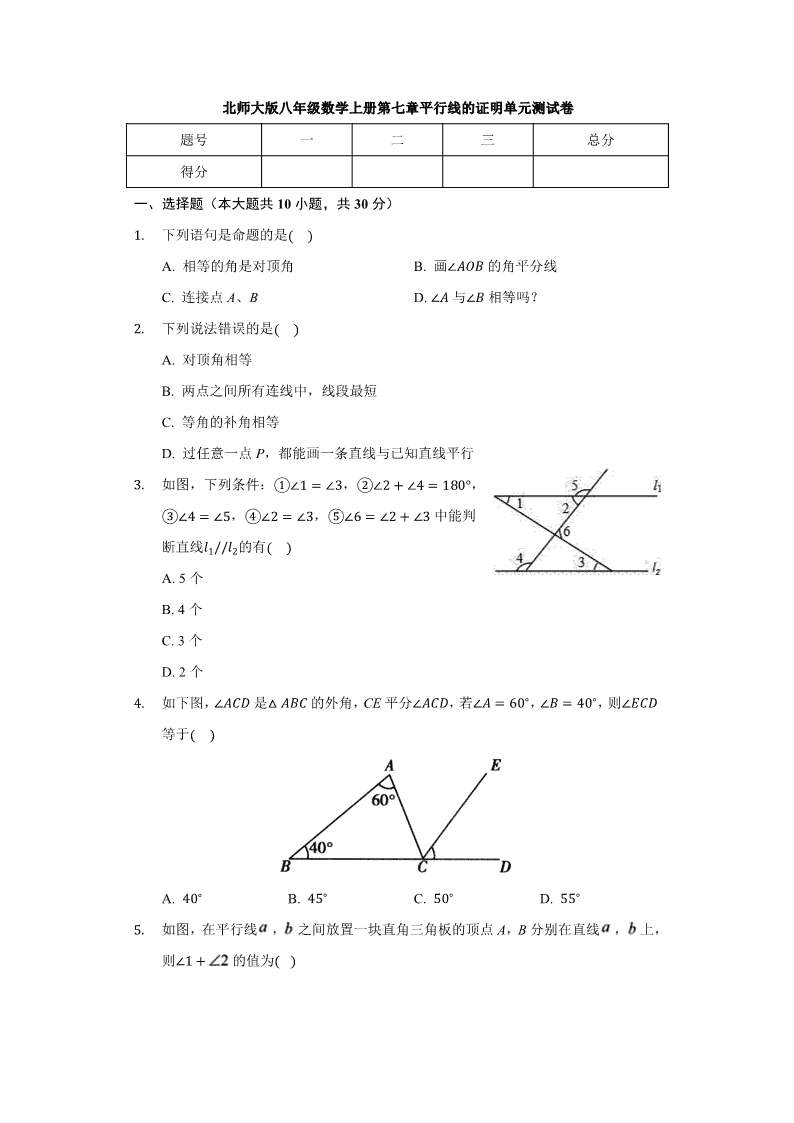
北师大版八年级数学上册第七章平行线的证明单元测试卷 题号 一 二 三 总分 得分 一、选择题（本大题共 10 小题，共 30 分） 1. 下列语句是命题的是 A. 相等的角是对顶角 B. 画ᦙ䁡的角平分线 C. 连接点 A、B D. 与䁡相等吗？ 2. 下列说法错误的是 A. 对顶角相等 B. 两点之间所有连线中，线段最短 C. 等角的补角相等 D. 过任意一点 P，都能画一条直线与已知直线平行 3. 如图，下列条件：1 3，2 1ͳ， ，2 3， 2 3中能判 断直线12的有 A. 5个 B. 4个 C. 3个 D. 2个 . 如下图，ᦙ䁡是 䁡ᦙ的外角，CE平分ᦙ䁡，若 ，䁡 ，则ᦙ䁡 等于 A. B. C. D. . 如图，在平行线 ， 之间放置一块直角三角板的顶点 A，B分别在直线 ， 上， 则1 的值为 A. B. C. D. . 已知直线12，一块含 3角的直角三角板如图所示放置，1 3，则2等于 A. 2 B. 3 C. D. 7. “同角的补角相等”改写成“如果那么”的形式，正确的是 A. 如果同角，那么补角相等 B. 如果两个角相等，那么这两个角是同一个角的补角 C. 如果两个角是同角的补角，那么这两个角相等 D. 如果两个角互补，那么它们相等 ͳ. 如图，䁡䁡ᦙ，1 ͳ，2 37，则的度 数是 A. 15度 B. 37度 C. 48度 D. 53度 9. 下列命题中，假命题的是 A. 凡是直角都相等 B. 对顶角相等 C. 不相等的角不是对顶角 D. 同位角相等 1. 如图，AE平分 䁡ᦙ外角ᦙ䁡，且 䁡ᦙ，给出下列结论： 䁡 ᦙ；䁡 䁡；ᦙ ᦙ；䁡 ᦙ； ᦙ 䁡 1ͳ，其中正确的个数有 A. 5个 B. 4个 C. 3个 D. 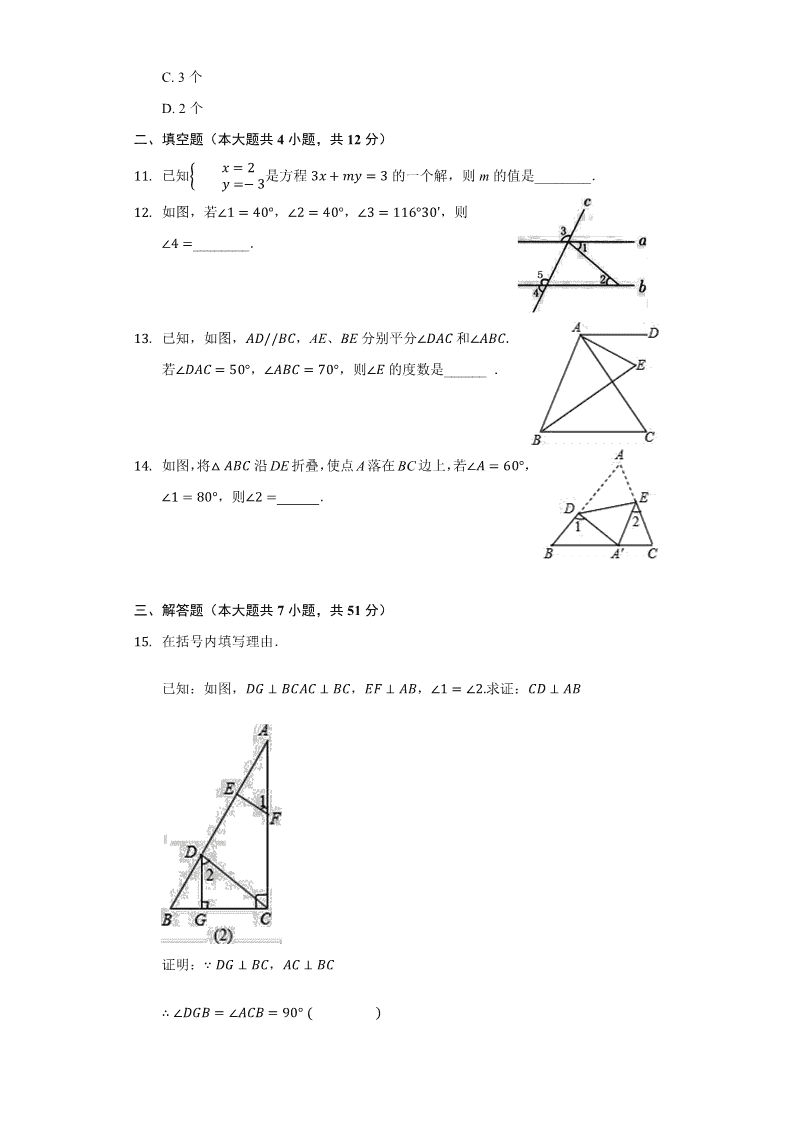2个 二、填空题（本大题共 4 小题，共 12 分） 11. 已知 2 3是方程 3 ൅ 3的一个解，则 m的值是________． 12. 如图，若1 ，2 ，3 113䁒，则 ________． 13. 已知，如图，䁡䁡ᦙ，AE、BE分别平分䁡ᦙ和䁡ᦙ. 若䁡ᦙ ，䁡ᦙ 7，则的度数是______ ． 1. 如图，将 䁡ᦙ沿DE折叠，使点A落在BC边上，若 ， 1 ͳ，则2 ______． 三、解答题（本大题共 7 小题，共 51 分） 1. 在括号内填写理由． 已知：如图，䁡 䁡ᦙᦙ 䁡ᦙ， 䁡，1 2.求证：ᦙ䁡 䁡 证明： 䁡 䁡ᦙ，ᦙ 䁡ᦙ 䁡䁡 ᦙ䁡 9 䁡ᦙ 2 䁡ᦙ 1 2 1 䁡ᦙ ᦙ䁡 䁡ᦙ 䁡 9 䁡ᦙ 9 即 ᦙ䁡 䁡． 16. 把下列命题改写成“如果那么”的形式． 1对顶角相等． 2两直线平行，同位角相等． 17. 如图，ᦙ䁡内有一点 P，过点 P画 ᦙᦙ䁡交 OA于点 C，画 䁡ᦙ交 OB于 点 D． 1根据题意画出图形； 2若ᦙ䁡 ，求ᦙ䁡的度数． 18. 已知：如图，䁡ᦙ 䁡ᦙ，BF和 DE分别平分䁡ᦙ 和䁡ᦙ，1 2.求证：䁡䁡． 19. 已知 䁡ᦙ的三条角平分线相交于点 I，过点 I作 䁡 ᦙ，交 AC于点 D． 1如图 1所示，求证：䁡 䁡． 2如图 2所示，延长 BI，交外角ᦙ的平分线于点 F． 判断 DI与 CF的位置关系，并说明理由； 若䁡ᦙ 7，求的度数． 20. 如图，已知 䁡䁡 ᦙ， ᦙ，点 D，F是垂足，1 2.求证：䁡 ᦙ． 答案和解析 1.【答案】A 【解析】 【分析】 本题考查命题与定理，掌握命题的意义是解决问题的关键.对事情做出正确或不正确的 判断的句子叫做命题.依据命题的定义进行判断即可． 【解答】 解：.相等的角是对顶角，是判断语句，故是命题； B.画ᦙ䁡的角平分线，不是判断语句，故不是命题； C.连接点 A、B，不是判断语句，故不是命题； D.与䁡相等吗？不是判断语句，故不是命题． 故选 A． 2.【答案】D 【解析】 【分析】 此题考查平行线公理，关键是根据对顶角、线段的性质、补角的性质和平行线的概念解 答． 根据对顶角、线段的性质、补角的性质和平行线的概念判断即可． 【解答】 解：A、对顶角相等，正确，故此选项不符合题意； B、两点之间所有连线中，线段最短，正确，故此选项不符合题意； C、等角的补角相等，正确，故此选项不符合题意； D、过直线外一点 P，能且只能画一条直线与已知直线平行，D选项的说法错误，故此 选项符合题意． 故选 D． 3.【答案】B 【解析】 【分析】 本题考查的是平行线的判定，熟记平行线的判定定理是解答此题的关键．根据平行线的 判定定理对各小题进行逐一判断即可． 【解答】 解： 1 3， 12内错角相等，两直线平行故本小题正确； 2 1ͳ， 12同旁内角互补，两直线平行故本小题正确； ， 12同位角相等，两直线平行故本小题正确； 2 3不能判定12，故本小题错误； 2 3， 2 1， 1 3， 12内错角相等，两直线平行 故本小题正确． 故选 B． 4.【答案】C 【解析】 【分析】本题考查了角平分线定义和三角形外角性质，能熟记三角形外角性质的内容是 解此题的关键.根据三角形外角性质求出ᦙ䁡，根据角平分线定义求出即可． 【解答】解： ，䁡 ， ᦙ䁡 䁡 1， ᦙ平分ᦙ䁡， ᦙ䁡 1 2 ᦙ䁡 ， 故选 C． 5.【答案】A 【解析】 【分析】 本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键． 过点 C作 ᦙ䁡，再由平行线的性质即可得出结论． 【解答】 解：过点 C作 ᦙ䁡，则1 ᦙ䁡． 㠲， ᦙ䁡㠲， 2 䁡ᦙ䁡． ᦙ䁡 䁡ᦙ䁡 9， 1 2 9． 故选 A． 6.【答案】A 【解析】 【分析】 本题考查的是平行线的性质及三角形外角的性质，用到的知识点为：两直线平行，同位 角相等． 先根据三角形外角的性质求出3的度数，再由平行线的性质得出的度数，由直角三 角形的性质即可得出结论． 【解答】 解：如图， 3是 䁡的外角， 3 1 3 3 ， 12， 3 ， ᦙ 9， ᦙ 9 2， 2 2． 故选 A． 7.【答案】C 【解析】 【分析】 本题考查了命题的知识，分辨出命题的题设与结论是解题的关键． 根据命题是题设与结论两部分组成改写，然后选择答案即可． 【解答】 解：“同角的补角相等”改写成“如果两个角是同角的补角，那么这两个角相等 ”． 故选 C． 8.【答案】C 【解析】 【分析】 根据平行线的性质，得出䁡䁡ᦙ 1 ͳ，再根据三角形外角性质，得出 䁡䁡ᦙ 2 ͳ 37 ͳ即可． 本题主要考查了平行线的性质以及三角形外角性质的运用，解决问题的关键是掌握：三 角形的一个外角等于和它不相邻的两个内角的和． 【解答】 解： 䁡䁡ᦙ，1 ͳ， 䁡䁡ᦙ 1 ͳ， 又 䁡䁡ᦙ是 䁡䁡的外角， 䁡䁡ᦙ 2 ͳ 37 ͳ， 故选：C． 9.【答案】D 【解析】 【分析】 本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题.根据直 角的定义，对顶角的性质、平行线的性质定理判断． 【解答】 解：.凡是直角都相等，是真命题，故 A不合题意； B.对顶角相等，是真命题，故 B不合题意； C.不相等的角不是对顶角，是真命题，故 C不合题意； D.同位角不一定相等，是假命题，故 D符合题意． 故选 D． 10.【答案】A 【解析】 【分析】 本题主要考查了平行线的性质与角平分线的定义，此题比较简单，解题的关键是注意掌 握两直线平行，同位角相等，两直线平行，内错角相等与两直线平行，同旁内角互补定 理的应用，注意数形结合思想的应用.利用角平分线的性质结合平行线的性质分别得出 䁡 䁡，ᦙ ᦙ，䁡 䁡 1ͳ，进而分别求得答案． 【解答】 解： 平分ᦙ䁡， 䁡 ᦙ，故正确， 䁡ᦙ， 䁡 䁡，ᦙ ᦙ，䁡 䁡 1ͳ， 故正确， 结合得：䁡 ᦙ，ᦙ 䁡 1ͳ，故正确． 故选 A． 11.【答案】1 【解析】 【分析】 本题考查了二元一次方程的解，解决本题的关键是明确二元一次方程的解的定义，把 2 3代入方程 3 ൅ 3，即可解答． 【解答】 解： 2 3是方程 3 ൅ 3的一个解， 3൅ 3， 解得：൅ 1， 故答案为 1． 12.【答案】33䁒 【解析】 【分析】 此题主要考查了平行线的判定与性质，关键是掌握同位角相等，两直线平行．根据1 2可以判定 㠲，再根据平行线的性质可得3 ，再根据邻补角互补可得答案． 【解答】 解： 1 ，2 ， 㠲， 3 113䁒， 1ͳ 113䁒 33䁒， 故答案为 33䁒． 13.【答案】 【解析】解： 、BE分别平分䁡ᦙ和䁡ᦙ， 䁡 1 2 䁡ᦙ 2，ᦙ䁡 1 2 䁡ᦙ 3， 过点 E作 䁡䁡ᦙ交 AB于点 F， 由平行线的性质，䁡 ，ᦙ䁡 䁡， 䁡 䁡 ᦙ䁡 2 3 ． 故答案为： 先根据 AE、BE分别平分䁡ᦙ和䁡ᦙ，得到䁡 1 2 䁡ᦙ 2，ᦙ䁡 1 2 䁡ᦙ 3，过点 E作 䁡䁡ᦙ交 AB于点 F，再根据 䁡䁡ᦙ，得到 䁡 ᦙ䁡，据此进行计算即可． 本题主要考查了平行线的性质以及角平分线的定义的运用，解题时注意：两直线平行， 内错角相等． 14.【答案】 【解析】解：将 䁡ᦙ沿 DE折叠，使点 A落在 BC边上， 䁡䁒 ， 䁡 ᦙ 䁡䁒 䁡䁒 1ͳ 12， 2 3 1 䁡 ᦙ 䁡䁒 䁡䁒 3 ͳ 12 12 ， 故答案为：． 本题考查了翻折问题，根据三角形内角和是 1ͳ是解答此题的关键．先根据图形翻折 变换的性质得出䁡䁒的度数，再根据三角形内角和定理求出䁡 ᦙ和䁡䁒 䁡䁒的度数，再由四边形的内角和为 3即可得出结论． 15.【答案】垂直的性质；同位角相等，两直线平行；两直线平行，内错角相等；等量 代换；两直线平行，同位角相等 【解析】 【分析】 本题主要考查平行线的性质与判定，垂线的性质，利用垂直的定义除了由垂直得直角外， 还能由直角判定垂直，判断两直线的夹角是否为 9是判断两直线是否垂直的基本方 法．由已知条件结合图形再灵活运用垂直的定义，注意由垂直可得 9角，由 9角可 得垂直，结合平行线的判定和性质，只要证得䁡ᦙ 9，即可得 ᦙ䁡 䁡． 【解答】 解： 䁡 䁡ᦙ，䁡ᦙ ᦙ已知 䁡䁡 䁡ᦙ 9垂直的性质 䁡ᦙ，同位角相等，两直线平行 2 䁡ᦙ，两直线平行，内错角相等 1 2已知 ， 1 䁡ᦙ，等量代换 䁡ᦙ， 䁡ᦙ两直线平行，同位角相等， 䁡已知， 9垂直定义， 䁡ᦙ 9等量代换， 即：ᦙ䁡 䁡， 故答案为垂直的性质，同位角相等，两直线平行，两直线平行，内错角相等，等量代换， 两直线平行，同位角相等． 16.【答案】解：1如果两个角是对顶角，那么这两个角相等． 2如果两条平行线被第三条直线所截，那么同位角相等． 【解析】本题主要考查了将原命题写成条件与结论的形式，“如果”后面是命题的条件， “那么”后面是条件的结论，解决本题的关键是找到相应的条件和结论，比较简单．根 据任何一个命题都可以写成“如果，那么”的形式，如果后面是题设，那么后面是 结论，进而得出答案即可． 17.【答案】解： 䁡ᦙ， ᦙ䁡 ， 又 ᦙ平分ᦙ䁡， ᦙ䁡 2ᦙ䁡 1， ᦙ䁡是 䁡ᦙ的外角， 䁡 ᦙ䁡 1 ． 故䁡的度数为 ． 【解析】本题主要考查了三角形外角的性质，平行线的性质以及角平分线的性质，求出 䁡ᦙ的外角ᦙ䁡 1是解题的关键，然后利用三角形外角的性质即可得到答案． 18.【答案】解：1如图即为所求图形： 2 ᦙᦙ䁡， ᦙ ᦙ䁡， 又 䁡ᦙ， ᦙ ᦙ䁡， ᦙ䁡 ， ᦙ䁡 ᦙ䁡 ， ᦙ䁡 ． 【解析】此题主要平行线的画法，以及平行线的性质，对顶角的性质，关键是掌握两直 线平行，同位角相等，内错角相等． 1根据平行线的画法作出 ᦙᦙ䁡；根据平行线的画法作出 䁡ᦙ； 2根据两直线平行，同位角相等，内错角相等进行运算即可． 19.【答案】证明： 䁡、DE分别平分䁡ᦙ与䁡ᦙ， 䁡ᦙ 2䁡，䁡ᦙ 22， 䁡ᦙ 䁡ᦙ， 䁡 2， 1 2， 䁡 1， 䁡䁡． 【解析】本题主要考查平行线的判定和性质及角平分线的定义，掌握平行线的判定和性 质是解题的关键，即同位角相等两直线平行，内错角相等两直线平行，同 旁内角互补两直线平行， 由条件䁡ᦙ 䁡ᦙ和角平分线的定义，可证明 䁡䁡． 20.【答案】1证明： 、BI分别平分䁡ᦙ，䁡ᦙ， 䁡 1 2 䁡ᦙ，䁡 1 2 䁡ᦙ， 䁡 䁡 1 2 䁡ᦙ 䁡ᦙ 1 2 1ͳ ᦙ䁡 9 1 2 ᦙ䁡， 在 䁡中，䁡 1ͳ 䁡 䁡 1ͳ 9 1 2 ᦙ䁡 9 1 2 ᦙ䁡， ᦙ平分ᦙ䁡， 䁡ᦙ 1 2 ᦙ䁡， 䁡 ᦙ， 䁡ᦙ 9， 䁡 䁡ᦙ 䁡ᦙ 9 1 2 ᦙ䁡， 䁡 䁡． 2解：结论：䁡ᦙ． 理由： 䁡ᦙ 9 䁡ᦙ 9 1 2 ᦙ䁡， ᦙ平分ᦙ， ᦙ 1 2 ᦙ 1 2 1ͳ ᦙ䁡 9 1 2 ᦙ䁡， 䁡ᦙ ᦙ， 䁡ᦙ． 解： ᦙ 䁡ᦙ 䁡ᦙ， ᦙ 䁡ᦙ 䁡ᦙ 7， ᦙ 䁡ᦙ ， ᦙ 䁡ᦙ， ᦙ 1 2 ᦙ，䁡ᦙ 1 2 䁡ᦙ， 1 2 ᦙ 1 2 䁡ᦙ 1 2 ᦙ 䁡ᦙ 3 【解析】本题考查三角形的内角和定理、三角形的外角的性质、平行线的判定等知识， 解题的关键是灵活运用所学知识解决问题，属于中考常考题型． 1只要证明䁡 9 1 2 ᦙ䁡，䁡 9 1 2 ᦙ䁡即可； 2只要证明䁡ᦙ 䁡ᦙ即可； 首先求出ᦙ 䁡ᦙ 䁡ᦙ 7，再证明 1 2 ᦙ 1 2 䁡ᦙ 1 2 ᦙ 䁡ᦙ即可解决问题； 21.【答案】证明： 䁡䁡 ᦙ， ᦙ， 䁡䁡ᦙ ᦙ 9， 䁡䁡， 2 ᦙ䁡䁡， 1 2， 1 ᦙ䁡䁡， 䁡䁡ᦙ， 䁡 ᦙ． 【解析】此题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解本题的关 键． 由 BD与 EF都与 AC垂直，利用垂直于同一条直线的两直线平行得到 BD与 EF平行， 利用两直线平行同位角相等得到一对角相等，再由已知的一对角相等，等量代换得到一 对内错角相等，利用内错角相等两直线平行得到 DG与 BC平行，利用两直线平行同位 角相等即可得证．