八年级下数学课件八年级下册数学课件《线段的垂直平分线》 北师大版 (1)_北师大版 43页

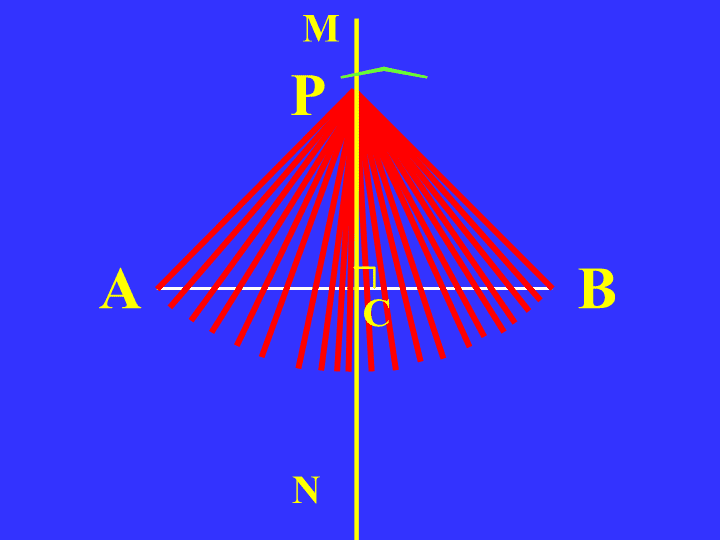
线段的垂直平分线 问题:如图,A、B、C三个村庄合建一所学校,要求校址P点距离三个村庄都相等.请你帮助确定校址.ABC ABMNCP MNCABQ ABMNP.Q.C 你能用不同的方法验证这一结论吗？探索并证明线段垂直平分线的性质如图，直线l垂直平分线段AB，P1，P2，P3，…是l上的点，请猜想点P1，P2，P3，…到点A与点B的距离之间的数量关系．相等．ABlP1P2P3 探索并证明线段垂直平分线的性质请在图中的直线l上任取一点，那么这一点与线段AB两个端点的距离相等吗？线段垂直平分线上的点与这条线段两个端点的距离相等．ABlP1P2P3 线段垂直平分线上的点和这条线段两个端点的距离相等.定理(线段垂直平分线的性质定理) 线段垂直平分线上的点和这条线段两个端点的距离相等.定理 线段垂直平分线上的点和这条线段两个端点的距离相等.定理 线段垂直平分线上的点和这条线段两个端点的距离相等.定理 直线MNAB，垂足是C，且AC=CB.点P在MN上.已知：PA=PB求证：ABCNMP 证明:∵MNAB（已知）∴PCA=PCB(垂直的定义)在PCA和PCB中,AC=CB(已知),PCA=PCB(已证)PC=PC(公共边)∴PCA≌PCB(SAS)∴PA=PB(全等三角形的对应边相等)ABCMNP 线段垂直平分线上的点和这条线段两个端点的距离相等.定理 8课堂练习练习1如图，在△ABC中，BC=8，AB的中垂线交BC于D，AC的中垂线交BC与E，则△ADE的周长等于______．ABCDE 解：∵AD⊥BC，BD=DC∴AD是BC的垂直平分线∴AB=AC∵点C在AE的垂直平分线上∴AC=CE．∴AB=AC=CE课堂练习P622如图，AD⊥BC，BD=DC，点C在AE的垂直平分线上，AB，AC，CE的长度有什么关系？AB+BD与DE有什么关系？ABCDE∵AB=CE，BD=DC，∴AB+BD=CD+CE．即AB+BD=DE． 已知线段AB,有一点P,并且PA=PB.那么,点P是否一定在AB的垂直平分线上?PABMNCP/这样的点P/不存在 探索并证明线段垂直平分线的判定反过来，如果PA=PB，那么点P是否在线段AB的垂直平分线上呢？点P在线段AB的垂直平分线上．已知：如图，PA=PB．求证：点P在线段AB的垂直平分线上．PABC 探索并证明线段垂直平分线的判定证明：过点P作线段AB的垂线PC，垂足为C．则∠PCA=∠PCB=90°．在Rt△PCA和Rt△PCB中，∵PA=PB，PC=PC，∴Rt△PCA≌Rt△PCB（HL）．∴AC=BC．又PC⊥AB，∴点P在线段AB的垂直平分线上．PABC 探索并证明线段垂直平分线的判定用数学符号表示为：∵PA=PB，∴　点P在AB的垂直平分线上．与一条线段两个端点距离相等的点，在这条线段的垂直平分线上．PABC 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.逆定理 小结:1.线段的垂直平分线上的点,和这条线段两个端点的距离相等.2.和一条线段两个端点距离相等的点,在这条线段的垂直平分线上. ABCMN CABMN 和线段两个端点距离相等的所有点的集合.线段的垂直平分线可以看作是 解：∵AB=AC，∴　点A在BC的垂直平分线．∵MB=MC，∵　点M在BC的垂直平分线上，∴　直线AM是线段BC的垂直平分线．课堂练习练习3如图，AB=AC，MB=MC．直线AM是线段BC的垂直平分线吗？ABCDM 例已知:如图ABC中,边AB、BC的垂直平分线相交于点P.求证:PA=PB=PC.∴PA=PB(线段垂直平分线上的点和这条线段两个端点距离相等)证明:∵点P在线段AB的垂直平分线上(已知)同理PB=PC∴PA=PB=PC.ACBMPNM/N/ （1）为什么任意取一点K，使点K与点C在直线两旁？尺规作图(P62)如何用尺规作图的方法经过直线外一点作已知直线的垂线？（2）为什么要以大于的长为半径作弧？（3）为什么直线CF就是所求作的垂线？CABDKFE 问题:如图,A、B、C三个村庄合建一所学校,要求校址P点距离三个村庄都相等.请你帮助确定校址.ABCP点P为校址 作图题:如图,在直线l上求一点P,使PA=PBlBAP点P为所求作的点 填空：1.已知:如图,AD是ABC的高,E为AD上一点,且BE=CE,则ABC为三角形.ABCED1题图等腰 填空：1.已知:如图,AD是ABC的高,E为AD上一点,且BE=CE,则ABC为三角形.2.已知:等腰ABC,AB=AC,AD为BC边上的高,E为AD上一点,则BEEC.(填>、<或=号)ABCEDABCED1题图2题图等腰= 3.已知:如图,AB=AC,A=30o,AB的垂直平分线MN交AC于D,则1=,2=.ABCDMN30o1275o30o60o45o 填空：4.已知:如图,在ABC中,DE是AC的垂直平分线,AE=3cm,ABD的周长为13cm,则ABC的周长为cmABDCE3cm3cm1913cm 5.如图,CD、EF分别是AB、BC的垂直平分线.请你指出图中相等的线段有哪些?AD=BDCF=BFAC=BCCE=BE123CF=DF即:BF=CF=DFACEBFD 证明题:1.已知:ABC中,C=90,A=30o,BD平分ABC交AC于D.求证:D点在AB的垂直平分线上.ABCD证明:30o∵C=90o,A=30o(已知)∴ABC=60o(三角形内角和定理)∴A=ABD(等量代换)∴D点在AB的垂直平分线上.(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.)∵BD平分ABC(已知)∴ABD=30o(角平分线的定义)30o∴AD=BD(等角对等边) 证明题:2.已知:如图,线段CD垂直平分AB,AB平分CAD.求证:AD∥BC.ABCDO123证明:∵线段CD垂直平分AB(已知)∴CA=CB(线段垂直平分线的性质定理)∴1=3(等边对等角)又∵AB平分CAD(已知)∴1=2(角平分线的定义)∴2=3(等量代换)∴AD∥BC(内错角相等,两直线平行) 证明题:3.已知:如图,在ABC中,AB=AC,A=120o,AB的垂直平分线交AB于E,交BC于F.求证:CF=2BF.ABCEF30060O30030OCF=2AFAF=BFCF=2BF 线段垂直平分线上的点和这条线段两个端点的距离相等.和一条线段两个端点距离相等的点,在这条线段的垂直平分线上.线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合.小结： 作业:P952.3.4 证明题:4.已知:如图,AD平分BAC,EF垂直平分AD交BC的延长线于F,连结AF.求证:CAF=B.ABCDEF1234 ABCDEF1234∴1+2=4(等边对等角)又∵4=B+3(三角形的一个外角等于与它不相邻的两个内角的和)∴1+2=B+3∵AD平分BAC(已知)∴2=3(角平分线的定义)∴1=B即CAF=B.证明:∵EF垂直平分AD(已知)∴AF=DF(线段垂直平分线的性质定理) 如图,已知:AOB,点M、N.求作:一点P,使点P到AOB两边的距离相等,并且满足PM=PN...MNAOB.P点P为所求作的点