八年级下数学课件：18-1-2 平行四边形的判定 （共18张PPT）_人教新课标 18页

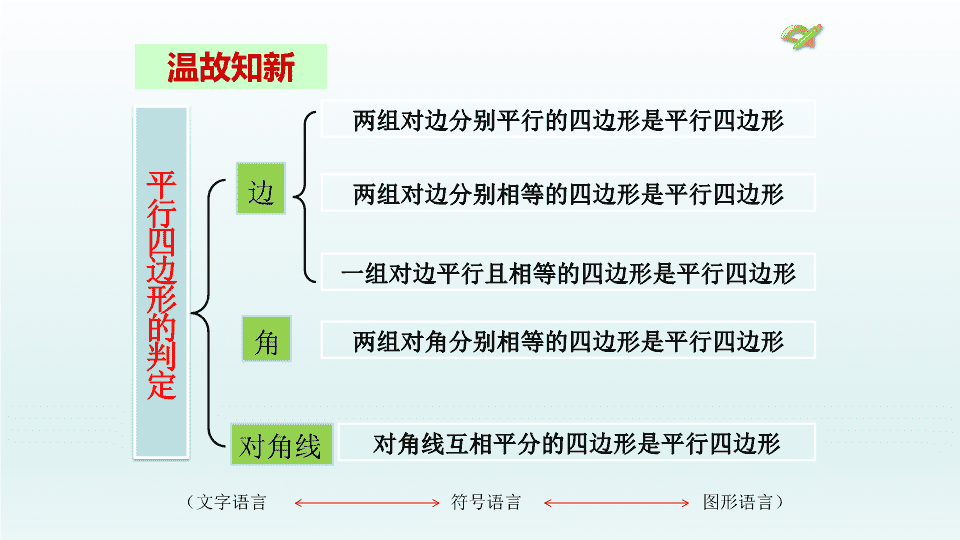
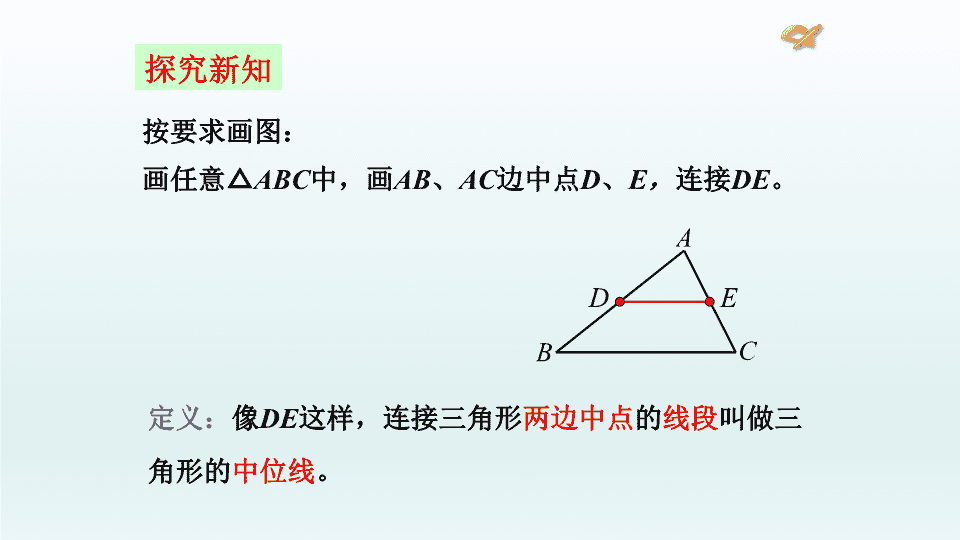
第十八章平行四边形§18.1平行四边形§18.1.2平行四边形的判定 温故知新平行四边形的判定边角对角线两组对边分别平行的四边形是平行四边形一组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形（文字语言符号语言图形语言） 探究新知按要求画图：画任意△ABC中，画AB、AC边中点D、E，连接DE。DE定义：像DE这样，连接三角形两边中点的线段叫做三角形的中位线。 探究思考问题1：一个三角形有几条中位线？DEF三条问题2：三角形中位线与三角形中线一样吗？DED端点不同 猜想与分析问题3：如图，DE是△ABC的中位线，DE与BC有怎样的关系？DE两条线段的关系位置关系数量关系分析：猜想：DE与BC的关系？度量一下你手中的三角形，看看是否有同样的结论？并用文字表述这一结论。问题4：DE∥BC， 归纳小结猜想：三角形的中位线平行于三角形的第三边且等于第三边的一半。DE问题5：如何证明你的猜想？ 探究思考已知，如图，D、E分别是△ABC的边AB、AC的中点.求证：DE∥BC，。DE 探究思考平行角平行四边形或线段相等一条线段是另一条线段的一半倍长短线分析1：DE 探究思考分析2：DE互相平分构造平行四边形倍长DE 思路点拔证明：DE延长DE到F，使EF=DE。连接AF、CF、DC。∵AE=EC，DE=EF，∴四边形ADCF是平行四边形F∴四边形BCFD是平行四边形。证法1：∴CFAD∴CFBD∴DFBC又∴DE∥BC，． DE思路点拔证明：延长DE到F，使EF=DE，F∴四边形BCFD是平行四边形∴△ADE≌△CFE∴∠ADE=∠F,连接FC。∵∠AED=∠CEF，AE=CE，(下面证明同证法1)证法2：ADCF∴BDCF 推出定理三角形的中位线平行于三角形的第三边且等于第三边的一半。DE△ABC中，若D、E分别是边AB、AC的中点，则DE∥BC，DE=BC。三角形中位线定理：（符号语言）（文字语言）（图形语言） 分析与归纳DE三角形的中位线平行一条线段是另一条线段的2倍或倍。三角形中位线定理： 学以致用1.如图，△ABC中，D、E分别是AB、AC中点。（1）若DE=5，则BC=。（2）若∠B=65°，则∠ADE=°。（3）若DE+BC=12，则BC=。1065x2x8 学以致用2.如图，A、B两点被池塘隔开，在AB外选一点C，连接AC和BC，怎样量出A、B两点间的距离？根据是什么？分别画出AC、BC中点M、N，量出M、N两点间距离，则AB=2MN。NM提示：根据是三角形中位线定理。 学以致用例：如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA中点。求证：四边形EFGH是平行四边形。四边形问题（连接对角线）三角形问题（三角形中位线定理） 归纳小结知识方面：1．三角形中位线概念；2．三角形中位线定理。思想方法方面：转化思想。 必做题：教材第49页练习第1、2题。选做题：再顺次连接本节课例题中所得到的四边形EFGH各边中点，又得到一个新的四边形，判断这个新四边形是否是平行四边形，并说明理由。安排作业