八年级下数学课件《矩形、菱形、正方形》 (10)_苏科版 21页

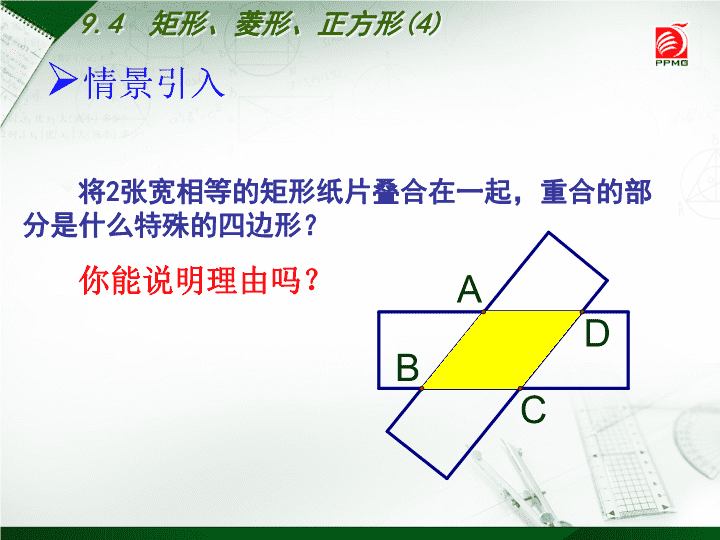
9.4矩形、菱形、正方形(4)八年级(下册)初中数学 将2张宽相等的矩形纸片叠合在一起，重合的部分是什么特殊的四边形？你能说明理由吗？情景引入9.4矩形、菱形、正方形(4) 根据菱形的定义,可得菱形的第一个判定的方法有一组邻边相等的平行四边形叫做菱形9.4矩形、菱形、正方形（4)数学语言:∴□ABCD是菱形∵在□ABCD中，AB=AD判定方法1： 命题：有四条边相等的四边形是菱形。已知：在四边形ABCD中,AB=BC=CD=DA.求证：四边形ABCD是菱形DABC证明：∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,9.4矩形、菱形、正方形(4)探究1∴ABCD是菱形 四条边相等的四边形是菱形.AB=BC=CD=DAABCD菱形ABCD∵在四边形ABCD中,AB=BC=CD=DA∴四边形ABCD是菱形四边形ABCDABCD判定方法2：数学语言9.4矩形、菱形、正方形(4) 命题：对角线互相垂直的平行四边形是菱形.已知：在中，AC⊥BDABCDABCD求证：是菱形ABCDO∟证明：∵四边形ABCD是平行四边形∴OA=OC又∵AC⊥BD;∴BA=BC∴ABCD是菱形9.4矩形、菱形、正方形(4)探究2∴BD是AC的垂直平分线 判定方法3：对角线互相垂直的平行四边形是菱形AC⊥BD∵在□ABCD中，AC⊥BD∴□ABCD是菱形ABCD菱形ABCDABCD□ABCD数学语言9.4矩形、菱形、正方形(4) 菱形常用的判定方法：有一组邻边相等的平行四边形叫做菱形对角线互相垂直的平行四边形是菱形有四条边相等的四边形是菱形。+邻边相等=+对角线互相垂直=四条边相等=归纳9.4矩形、菱形、正方形(4) 1、老师说下列三个图形都是菱形,你相信吗?5534345555有一组邻边相等的平行四边形叫做菱形对角线互相垂直的平行四边形是菱形有四条边相等的四边形是菱形。3344┍试一试9.4矩形、菱形、正方形(4) 2、如图：已知□ABCD的对角线AC与BD相交于点O，（1）若AB=AD，则□ABCD是_____形；（2）若AC=BD，则□ABCD是_____形；（3）若∠ABC是直角，则□ABCD是____形；（4）若∠BAO=∠DAO，则□ABCD是____形。ABCDO试一试9.4矩形、菱形、正方形(4) 9.4矩形、菱形、正方形(4)例1已知：如图，在四边形ABCD中，AD∥BC，对角线AC的垂直平分线与边AD、BC分别相交于点E、F．求证：四边形AFCE是菱形．ADBCEFO12例题讲解 例2、如图，ABCD的两条对角线AC、BD相交于点O，AB=5，AC=8，DB=6求证:四边形ABCD是菱形.ABCDO∴□ABCD是菱形.∴OA=OC=4OB=OD=3证明:又∵AB=5∴AC⊥BD∴∠AOB=90°又∵四边形ABCD是平行四边形∵四边形ABCD是平行四边形∴AB2=AO2+BO29.4矩形、菱形、正方形(4) 将2张宽相等的矩形纸片叠合在一起得到四边形ABCD（如图），你认为它是什么特殊的四边形？请说明理由？CDAB解决问题9.4矩形、菱形、正方形(4) 9.4矩形、菱形、正方形（4)你有其他用一张矩形纸片就能折出菱形的方法吗？能力拓展 1、如图，E、F、G、H分别是矩形ABCD各边的中点，四边形EFGH是怎样的特殊四边形？证明你的结论。9.4矩形、菱形、正方形(4) （2008•十堰）如图，把一张矩形的纸ABCD沿对角线BD折叠，使点C落在点E处，BE与AD交于点F．（1）求证：△ABF≌△EDF；（2）若将折叠的图形恢复原状，点F与BC边上的点M正好重合，连接DM，试判断四边形BMDF的形状，并说明理由．9.4矩形、菱形、正方形(4) （2013•郴州模拟）将矩形纸片ABCD折叠，使点C与点A重合，然后展开，折痕为EF，连接AE、CF，求证：四边形AECF是菱形．9.4矩形、菱形、正方形(4) 2、用直尺和圆规作一个菱形，并说明你作图的道理。9.4矩形、菱形、正方形(4)练一练1.课本P81第2题． 盘点收获通过本节课的学习，你有哪些收获？9.4矩形、菱形、正方形(4) 作业1.课本P84第9、10题．9.4矩形、菱形、正方形(4) 谢谢!9.4矩形、菱形、正方形(4)