八年级上数学课件八年级上册数学课件《整式的乘法》 人教新课标 (1)_人教新课标 12页

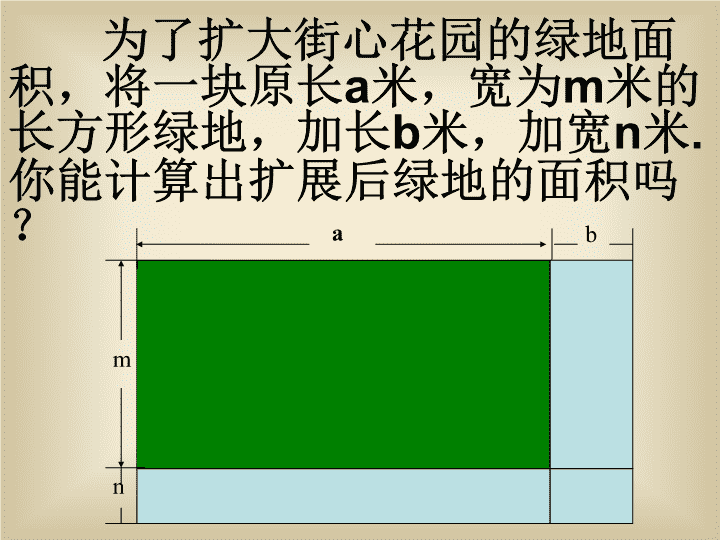
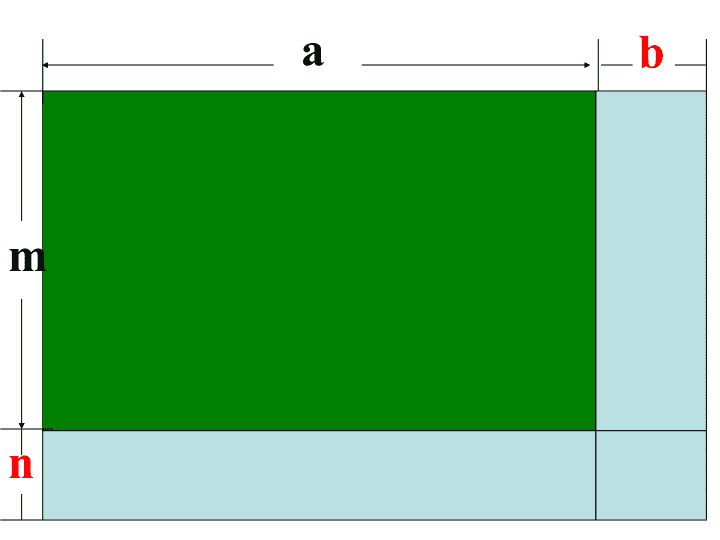
多项式乘以多项式 为了扩大街心花园的绿地面积，将一块原长a米，宽为m米的长方形绿地，加长b米，加宽n米.你能计算出扩展后绿地的面积吗？abmn abmn 观察上述式子,你能得到(x-3)(x-6)的结果吗?(x–3)(y–6)=x(y–6)–3(y–6)=xy–6x–3y+18 归纳得出:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn(a+b)(m+n)=a(m+n)+b(m+n)=am+an+bm+bn 例1计算：(1)(3x+1)(x–2);(2)(x–8y)(x–y).(3)(x+y)(x2-xy+y2) 练习:(1)(2x+1)(x+3);(2)(m+2n)(m+3n):(3)(a-1)2；(4)(a+3b)(a–3b).(5)(x+2)(x+3);(6)(x-4)(x+1)(7)(y+4)(y-2);(8)(y-5)(y-3) (x+2)(x+3)=x2+5x+6;(x-4)(x+1)=x2–3x-4(y+4)(y-2)=y2+2y-8(y-5)(y-3).=y2-8y+15观察上述式子，你可以得出一个什么规律吗？(x+p)(x+q)=x2+(p+q)x+pq P.150.12.确定下列各式中m的值:(x+p)(x+q)=x2+(p+q)x+pq 小结1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn2、多项式与多项式相乘时，多项式的每一项都应该带上它前面的正负号。多项式是单项式的和，每一项都包括前面的符号，在计算时一定要注意确定各项的符号。 4、在数学知识的学习中，“转化”思想是的重要思想方法。在今天的学习中，第一步是“转化”为多项式与单项式相乘，第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法。从而使学习能够进行。3、(x+p)(x+q)=x2+(p+q)x+pq 课外作业:课本P.150第11题解方程与不等式:(1)(x-3)(x-2)+18=(x+9)(x+1);(2)(3x+4)(3x-4)＜9(x-2)(x+3).